Select a year to see courses
Make the most of NESA Maths Reference Sheet and test your maths skills with these sample questions and explanations for vectors, complex numbers and mechanics!
Join 75,893 students who already have a head start.
"*" indicates required fields
The NESA Maths Reference Sheet is a great resource… if you know how to use it! Navigate vectors, complex numbers and mechanics with our Ultimate NESA Maths Reference Sheet Guide.
While memorisation has its place in learning, Matrix recommends that students learn to derive their responses and learn how to apply these formulae correctly. As a bonus, we’ve included a nifty HSC Maths Cheatsheet for you to download and print out!
Download your FREE Maths Formula Handbook
Click on the following formulas to see what they mean and apply them to a practice question!
| Vectors |
| \( |{\bf u}|=|x{\bf i}+y{\bf j}|=\sqrt{x^2+y^2} \) \({\bf u} \cdot {\bf v} = |{\bf u}||{\bf v}|\text{cos} \theta = x_1 x_2 + y_1 y_2 , \) \begin{align*} |
Maths Extension 2 only:
| Mechanics |
| \(\frac{d^2x}{dt^2} = \frac{dv}{dt} = v \frac{dv}{dx} = \frac{d}{dx} \left( \frac{1}{2} v^2 \right)\) |
| Use | Formula | Explanation |
| Magnitude of the vector | \( |{\bf u}|=|x{\bf i}+y{\bf j}|=\sqrt{x^2+y^2} \) | \begin{align*} |{\bf u}| &= \text{length/magnitude of }{\bf u} \\ (x, \ y) &= \text{ Cartesian coordinates of position vector } {\bf u} \\ {\bf i}&: \text{ unit vector in the direction of the x-axis} \\ {\bf j}&: \text{ unit vector in the direction of the y-axis} \\ \end{align*}  |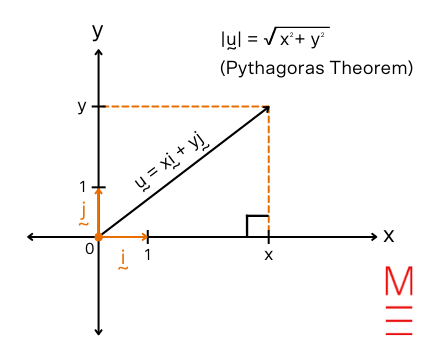
| Dot product | \({\bf u} \cdot {\bf v} = |{\bf u}||{\bf v}|\text{cos} \theta = x_1 x_2 + y_1 y_2 , \)\begin{align*} \text{where } {\bf u} &= x_1 {\bf i} + y_1{\bf j}\\ \text{and } {\bf v} &= x_2{\bf i} + y_2{\bf j}\\ \end{align*} |  |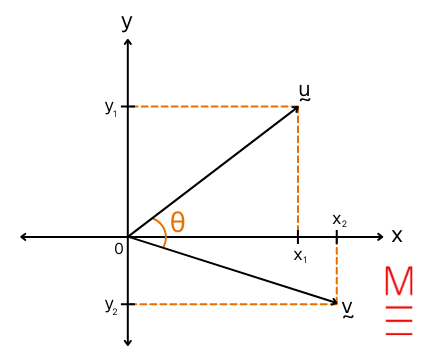
| Vector form of a line | \({\bf r}={\bf a} + λ {\bf b}\) | A line can be expressed in many different forms like Cartesian form (\(y =mx+c\)) and vector form. When we express line \({\bf r}\) in vector form, we describe it using a point \({\bf a}= \binom{x}{y}\) that it passes through and its gradient vector \({\bf b}\). By substituting different constant values for \(λ∈R\), the vector equation \({\bf r}={\bf a} + λ {\bf b}\) describes every single point on line \({\bf r}\).
|
Example 28:
Express the line y = 4x + 3 in vector form.
Solution 28:
| Find a point that y = 4x + 3 passes through: \begin{align*}
Find a gradient vector of the line y = 4x + 3: Since the equation of the line is in the form y = mx + c, the gradient is the coefficient of x. \begin{align*} Now that we know that the line passes through \(\binom{1}{7}\) and has a gradient vector of \(\binom{1}{4}\), we can express the line in vector form: \({\bf r}= \binom{1}{7} + λ \binom{1}{4}\) where \(λ∈R\) |
Maths Extension 2 only:
| Use | Formula | Explanation |
| Manipulating expressions for acceleration, velocity and displacement | \(\frac{d^2x}{dt^2} = \frac{dv}{dt} = v \frac{dv}{dx} = \frac{d}{dx} \left( \frac{1}{2} v^2 \right)\) | Need help understanding differentiation? See the following Maths Guides! Maths Adv Applications of differentiation Maths Ext 1 |
| Expression for displacement \(x\) in terms of time \(t\) | \(x=a \text{cos} (nt+α)+c\) | \begin{align*} x & = \text{displacement} \\ \\ \ \frac{2\pi}{n} &= \text{Period} \\ a &= \text{Amplitude}\\ α &= \text{Phase shift}\\ c &= \text{Centre of motion} \end{align*} |
| \(x=a \text{sin} (nt+α)+c\) | ||
| Expression for acceleration \( \ddot x\) in terms of displacement \(x\) | \( \ddot x= -n^2(x-c)\) | \(\ddot x = \text{acceleration}\) |
Written by Matrix Maths Team
The Matrix Maths Team are tutors and teachers with a passion for Mathematics and a dedication to seeing Matrix Students achieving their academic goals.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
