Welcome to Matrix Education
To ensure we are showing you the most relevant content, please select your location below.
Select a year to see courses
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Get HSC Trial exam ready in just a week
Get HSC exam ready in just a week
Select a year to see available courses
Science guides to help you get ahead
Science guides to help you get ahead
Make the most of NESA Maths Reference Sheet and test your maths skills with these sample questions and explanations for measurement and financial maths!
Join 75,893 students who already have a head start.
"*" indicates required fields
Related courses

Join 8000+ students each term who already have a head start on their school academic journey.
The NESA Maths Reference Sheet is a great resource… if you know how to use it! Navigate measurement and financial mathematics with our Ultimate NESA Maths Reference Sheet Guide.
While memorisation has its place in learning, Matrix recommends that students learn to derive their responses and learn how to apply these formulae correctly. As a bonus, we’ve included a nifty HSC Maths Cheatsheet for you to download and print out!
Download your FREE Maths Formula Handbook
All the key Maths formulas you need to revise, in one foldable cheatsheet. Fill out your details below to get this resource emailed to you. "*" indicates required fields
A free pocket-sized Maths handbook, so you're prepared.

A free pocket-sized Maths handbook, so you're prepared.
Click on the following formulas to see what they mean and apply them to a practice question!
| Measurement | |
| Length \(l=\frac{\theta}{360}\times2\pi r\)
| Surface area
|
| Financial Mathematics |
| \(A= P(1+r)^n\)
\(S_n=\frac{n}{2} [2a+(n-1)d] = \frac{n}{2}(a+l)\) |
Back to top
Next section: Area
Example 1:
Find the length of the minor arc AB, such that the length of radius OA is 30 cm. Leave your answer as an exact value.
Solution 1:
| Substitute \(\theta = \text{115}\) and \(r = \text{30}\) into \(l=\frac{\theta}{360}\times2\pi r\): \begin{align*} |
| Use | Formula | Variables |
| Area of a sector | \(A= \frac{\theta}{360} \times \pi r^2\) | \begin{align*} A&= \text{area of sector}\\ \theta &= \text{angle of sector in degrees}\\ r &= \text{radius}\\ \end{align*} 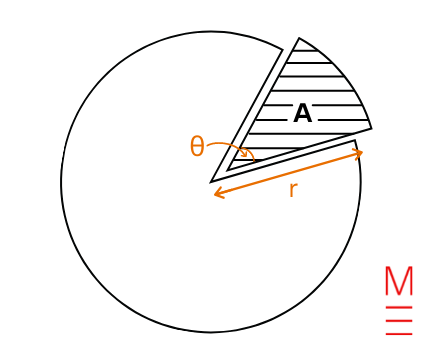 |
Back to top
Next section: Surface Area
Example 2:
Given that the following circle has a radius of 5 m, find the area of the major sector AOB. Leave your answer as an exact value.
Solution 2:
| Substitute \(\theta=330\) and \(r=5\) into \(A= \frac{\theta}{360} \times \pi r^2\): \begin{align*} |
Example 3:
What is the area of the shape below? Note that all the measurements were made in millimetres.
Solution 3:
| Substitute \(h=12\), \(a=16\) and \(b=20\) into \(A=\frac{h}{2} (a+b) \): \begin{align*} |
| Use | Formula | Variables |
| Surface area of a cylinder | \(A=2 \pi r^2 + 2 \pi r h \) | \begin{align*} A&= \text{surface area of cylinder}\\ h &= \text{height}\\ r &= \text{radius of circular base}\\ \end{align*} 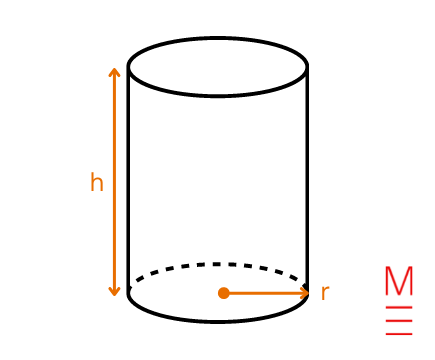 |
Back to top
Next section: Volume
Example 4:
Gemma is designing a can for her new spaghetti recipe. In order to figure out how much pink paint she needs to completely cover the can, she needs to know what the total surface area of the cylindrical can is.
Knowing that the dimensions below are given in centimetres, what is the surface area of Gemma’s can? Leave your answer as an exact value.
Solution 4:
| Substitute \(h=9\) and \(r=4\) into \(A=2 \pi r^2 + 2 \pi r h \): \begin{align*} |
Example 5:
Biological cells with larger surface area to volume ratios are able to more efficiently diffuse oxygen into the cell and waste material out.
If we approximate a cell to be the shape of a sphere, what is the surface area of a cell with a diameter of 0.07 mm? Leave your answer as an exact value.
Solution 5:
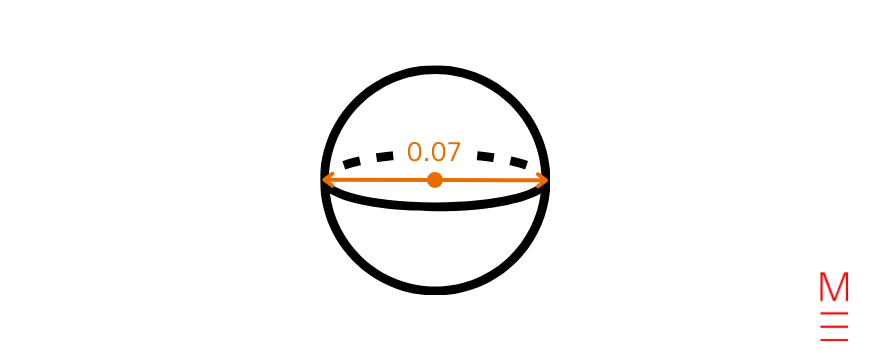 Substitute \(r= \frac{0.07}{2}\) (since the radius is half of the diameter) into \(A = 4 \pi r^2\): \begin{align*} |
| Use | Formula | Variables |
| Volume of a pyramid/cone | \(V= \frac{1}{3}Ah\) | \begin{align*} V &= \text{volume of pyramid/cone}\\ A &= \text{base area}\\ h &= \text{height}\\ \end{align*} 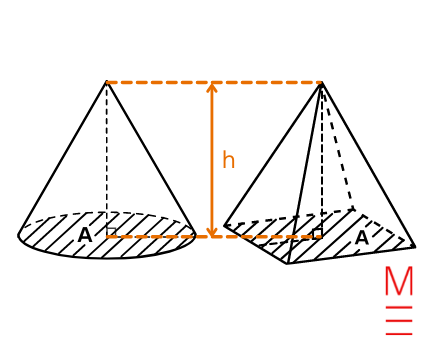 |
Back to top
Next section: Financial Mathematics
Example 6:
Ricky is planning her birthday party. She wants to prank her friends by putting water balloons inside all of the party hats.
Assuming that the party hats are a perfect cone with a radius of 5 cm and a height of 12 cm, how much water does she need to fill one party hat? Leave your answer as an exact value.
Solution 6:
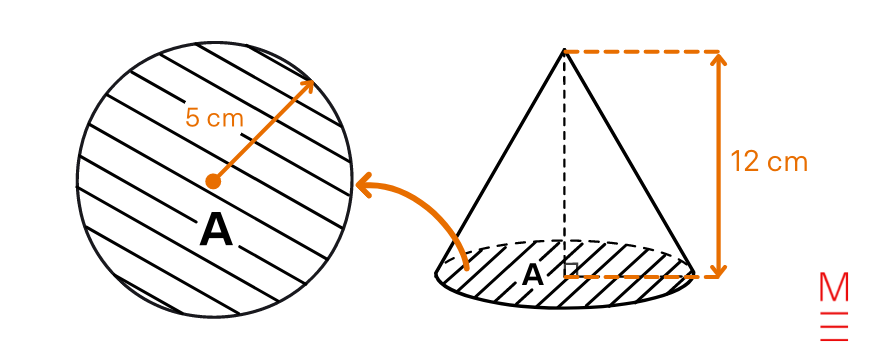 To find the area of the circular base, substitute \(r=5\) into \(A= \pi r^2\): \begin{align*}
Substitute \(A= 25 \pi\) and \(h=12\) into \(V= \frac{1}{3}Ah\): \begin{align*} |
Example 7:
Gordon is making meatballs. Assuming that 1 cm3 = 1 gram, how much mince does he need to make a perfectly spherical meatball with a diameter of 3 cm? Leave your answer as an exact value.
Solution 7:
| Substitute \(r= \frac{3}{2}\) (since the radius is half of the diameter) into \(V= \frac{4}{3} \pi r^3\): \begin{align*} |
Back to top
Next section: Sequences and series
Example 8:
Jacky’s bank is offering her a fantastic interest rate of 3% per annum, compounded every three months. If she deposits $12 360 into her savings account today and resolves to not take away from or add to these funds, what will be her savings account balance in 12 months time? Provide your answer to the nearest two decimal places.
Solution 8:
| \begin{align*} A & = \text{Jacky’s savings account balance in 12 months time: this is what we are trying to find!} \\ P & = 12 \ 360 \\ \end{align*}The interest rate of 3% per year is compounded every three months. So, we need to divide the 3% interest rate by the number of three month periods in 12 months to find the compound interest rate per three month period:\begin{align*} r & = \frac{3 \text{%}}{ \frac{12}{3} } \\ & = \frac{0.03}{4} \\ ∴r & = 0.0075 \\ \end{align*}Since the compounding period is three months and Jacky plans to leave her savings account balance as it is for 12 months:\begin{align*} n & = \frac{12}{3} \\ ∴n & = 4 \\ \end{align*}Hence, substitute \(P=12 \ 360\), \(r=0.0075\) and \(n=4\) into \(A= P(1+r)^n\):\begin{align*} A &= 12 \ 360 \times (1+0.0075)^4 \\ &= 12 \ 360 \times 1.0075^4 \\ &= 12 \ 734.99 \text{ (to the nearest two decimal places)} \\ ∴ \text{Jacky’s savings account balance in 12 months time} &= $12 \ 734.99\\ \end{align*} |
Test your knowledge with 4 levels of increasing difficulty. Fill out your details below to get this resource emailed to you. "*" indicates required fields
Download your free Financial Maths worksheet

Download your free Financial Maths worksheet
Note: A series is the sum of the elements in a sequence.
In an arithmetic progression, each term is determined by adding a constant to the preceding term.
Example 9:
Consider the following arithmetic sequence:
\( 3, 15, 27, 39… \)
What is the 23rd term of this sequence?
Solution 9:
| Substitute \(n=23\), \(a=3\) and \(d=12\) into \(T_n = a+(n-1)d\) \begin{align*} |
Example 10:
The sum of the first 16 terms of an arithmetic series is 632. Given the first term of the series is 2, write down the first 4 terms of the series.
Solution 10:
| Substitute \(S_n=632\), \(n=16\) and \(a=2\) into \(S_n=\frac{n}{2} [2a+(n-1)d] = \frac{n}{2}(a+l)\) \begin{align*} \begin{align*} |
In a geometric progression, each term is found by multiplying the previous term by a constant.
Example 11:
A basketball player is bouncing a ball. On each bounce, the ball reaches a height that is 85% of its previous height. The total distance that the ball has travelled just before they make contact with the ball for the 8th time is 6 metres.
a) At what height did the basketball player begin bouncing the ball? Give your answer in metres to the nearest three decimal places.
b) Hence or otherwise, find the total distance that the ball travels if the basketball player continues bouncing the ball until it eventually does not lift off the ground. Give your answer in metres to the nearest two decimal places.
Solution 11 a):
Solution 11 b):
| In part a), we found that the total distance d travelled by the ball is \(d = 2 \times S_n – T_1 – T_n\). Need a refresher? Click here to scroll up to the explanation in part a). In part a), we were interested in the distance that the ball travels before the 8th bounce. So, we used \(n = 8\). In part b) though, we are trying to find how far the ball can travel if it was allowed to bounce forever. So here, we let \(n = ∞\). Substitute \(n = ∞\) into \(d = 2 \times S_n – T_1 – T_n\): \begin{align*} Since: \begin{align*} \begin{align*} |
Review ‘Series and Sequences’ and download your free worksheet here.
Written by Matrix Maths Team
The Matrix Maths Team are tutors and teachers with a passion for Mathematics and a dedication to seeing Matrix Students achieving their academic goals.© Matrix Education and www.matrix.edu.au, 2025. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.