In this article, we will be utilising our knowledge of finding \(x\) – intercepts, \(y\) – intercepts and sketching various non-linear curves to sketch complicated Polynomial curves.
As you already know, a Polynomial is an algebraic expression made up of multiple terms. In this article, we will break down some complex Polynomial curves in a clear and accessible manner. We will then help you apply your knowledge with some concept check questions of varying difficulty at the end of the article.
Mastering Polynomial sketching plays an important role in being able to visualise certain graphs which will come up in later topics. It is one important part of understanding the nature behind various graphs and the effect different parts of an equation have on a final curve.
We’re going to look at the following NESA syllabus points.
NESA dictates that students need to learn the following concepts to demonstrate proficiency in Polynomials.
| \(a_n x^n+a_{n-1} x^{n-1}+⋯+a_2 x^2+a_1 x+a_0\) |
where \(n=0,1,2,…\) and \(a_0,a_1,a_2,…,a_n\) are real numbers
Students should already be familiar with function notation, domain and range, odd/even functions and graphing non-linear functions.
This content can be found in our Year 10 Guides should students want to refresh their understanding:
To begin with, let’s get a clearer understanding of what a Polynomial is.
A polynomial is an algebraic expression made up of many terms as seen in the equation below.
| \(P(x)=a_n x^n+a_{n-1} x^{n-1}+a_{n-2}x^{n-2}⋯+a_2 x^2+a_1 x+a_0\) |
It has four terms which need to be familiarized with as this determines what the polynomial graphs look like when we learn how to sketch it later. Let’s take a look at this equation and its individual parts and see how they work:
| Polynomial | Explanation |
| \(a_n x^n\) | The leading term is \( a_n x^n \) and is the term with the highest power. |
| \(n\) | The degree is the highest power in the polynomial expression. |
| \(a_n\) | \( a_n \) is the leading coefficient as it is connected to the term with the highest power. The other values \( a_{n-1},a_{n-2},a_3,a_2,a_1\) are all coefficients. |
| \(a_0\) | \( a_0 \) is the constant term. |
Below are some Polynomials you are already familiar with:
This is a linear expression which is also a polynomial of degree 1.
This is a quadratic expression which is also a polynomial of degree 2.
This is a cubic expression which is also a polynomial of degree 3.
This is a quartic expression which is also a polynomial of degree 4.
At Matrix, we provide you with quality resources and engaging, structured lessons taught by HSC Maths experts. Learn more about our Year 11 Maths courses now.
When sketching a polynomial, it’s important to find the \( x \)-intercepts and identify the nature of the roots as either single, double or triple roots.
Determine the nature of the roots for the following polynomial:
\( P(x)=(2x-5) (x+1)^2 (x-1)^3 \)When we calculate the \(x \)-intercepts for each polynomial, we let \(y=0\) leaving us with the equation:
\( 0=(2x-5) (x+1)^2 (x-1)^3 \)This leaves us with three equations to solve to find the \( x \)-intercepts:
\begin{align*}
(2x-5)=0 \\
(x+1)^2=0 \\
(x-1)^3=0
\end{align*}
\(x=\frac{5}{2}\). This is a single root because the power of the brackets is 1. As a single root, the curve will pass through the \(x\)-axis as follows:It’s important to note that the power of the brackets will impact the nature of the roots. Solving each equation, we get the following \( x \) -intercepts:
\(x=-1\). This is a double root because the power of the brackets is 2. As a double root, the curve will pass through the \(x\)-axis as follows:
\(x=1\). This is a triple root because the power of the brackets is 3. As a triple root, the curve will pass through the \(x\)-axis as follows:
If the polynomial curve has an odd degree and is positive, it will result in the curve beginning in the 3rd quadrant and ending in the 1st quadrant as follows:
If the polynomial curve has an odd degree and is negative, it will result in the curve beginning in the 2nd quadrant and ending in the 3rd quadrant as follows:
If the polynomial has an even degree and is positive, it will result in the curve beginning and ending in the 1st and 2nd quadrants as follows:
If the polynomial has an even degree and is negative, it will result in the curve beginning and ending in the 3rd and 4th quadrants as follows:
Consider the following process that we have broken down into 5 steps for sketching polynomials:
| Steps | Explanation |
| Step 1 | The degree of the polynomial. This will determine the general shape of the curve. |
| Step 2 | The \(x\) – intercepts of the curve. |
| Step 3 | The \(y\) – intercepts of the curve. |
| Step 4 | Determine the type of root for each \(x\) – intercept. This will reveal to you if the curve:
|
| Step 5 | Combine all this information and sketch it on the Cartesian plane. |
Now let’s put this into practice.
Sketch the following polynomial, clearly indicating all intercepts on the coordinate axes:
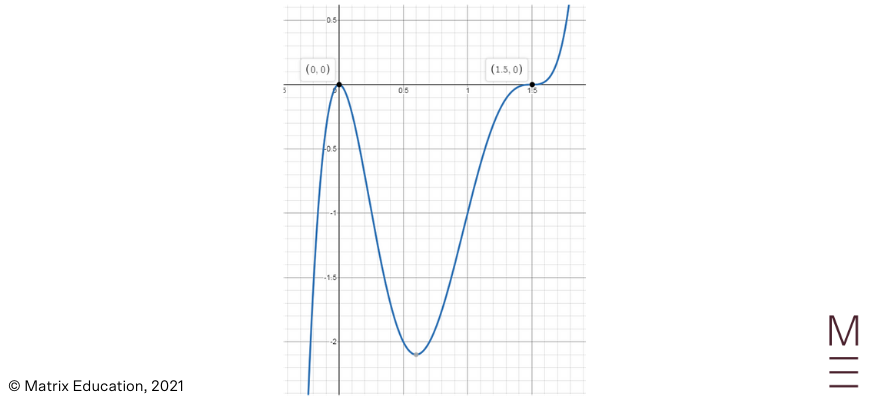
\(P(x)=(x-1)(x+1)(x+3)\)Step 1: Multiplying all the values together, the highest power of \(x\) will be \(3\). Therefore, this polynomial has a degree of \(3\) and will extend from the 3rd quadrant to the 1st quadrant.
Step 2: When finding the \(x\)-intercepts, let \(y=0\).
\(0=(x-1)(x+1)(x+3) \\ x=-3,-1,1\)
Step 3: When finding the \(y\) – intercepts, let \(x=0\).
\(P(0)=(0-1)(0+1)(0+3)=-3\)
Step 4: All of the \(x\)-intercepts have a single root.
Step 5: Therefore, placing all this information together we obtain the following graph:
Sketch the following polynomial, clearly indicating all intercepts on the coordinate axes:
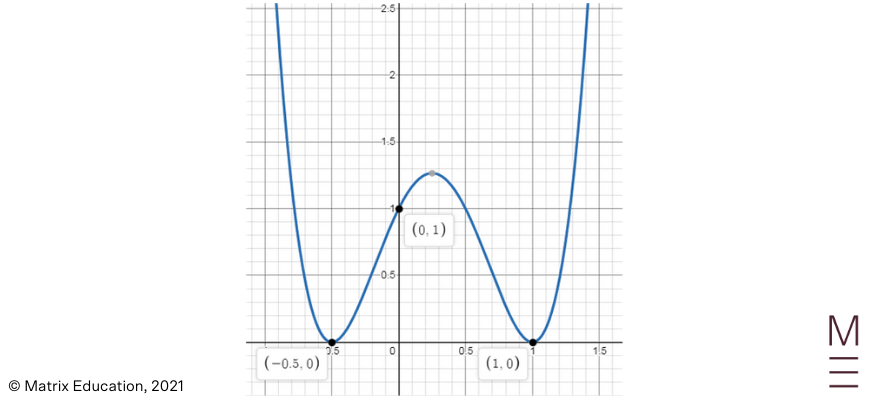
\(P(x)=(1-x) (x-3)^2 (x+1)\)Step 1: Multiplying all the values together, the highest power of \(x\) will be \(4\), and the coefficient will also be \(“-“\).
Therefore, this negative polynomial has a degree of \(4\) and will extend from the 1st quadrant to the 4th quadrant.
Step 2: When finding the \(x\) – intercepts, let \(y=0 \)
\(0=(1-x) (x-3)^2 (x+1) \\ x=-1,1,3\)
Step 3: When finding the y-intercepts, let \(x=0 \)
\(P(0)=(1-0) (0-3)^2 (0+1)=9\)
Step 4: The \(x\)-intercepts \(x=-1\) and \(1\) are singular roots, and the \(x\)-intercept \(x=3\) is a double root.
Step 5: Therefore, placing all this information together we obtain the following graph:
Sketch the following polynomial, clearly indicating all the intercepts on the coordinate axes:
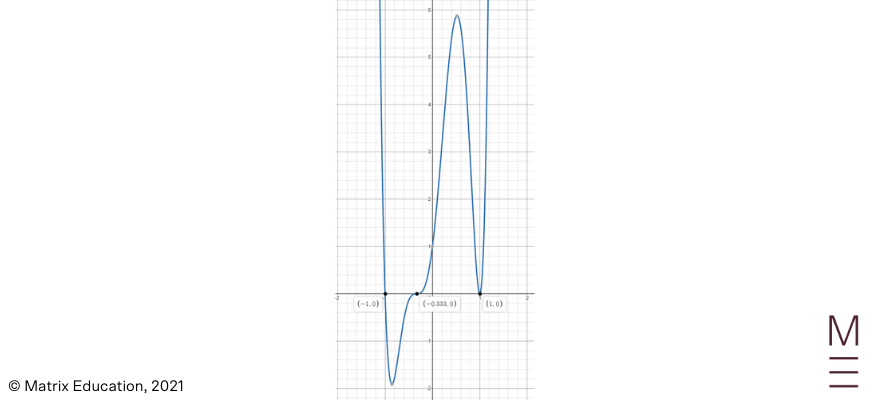
\(P(x)=x(x-2)^3 (x+1)^2\)Step 1: Multiplying all the values together, the highest power of \(x\) will be \(6\). Therefore, this polynomial has a degree of \(6\) and will extend from the 1st quadrant to the 3rd quadrant.
Step 2: When finding the \(x\)-intercepts, let \(y=0\)
\(0=x(x-2)^3 (x+1)^2 \\ x=-1,0,2\)
Step 3: When finding the \(y\)-intercepts, let \(x=0 \)
\(P(0)=0(0-2)^3 (0+1)^2=0\)
Step 4: The \(x\)-intercept \(x=0\) is a singular root, \(x=2\) is a triple root, and \(x=-1\) is a double root.
Step 5: Therefore, placing all this information together we obtain the following graph:
1. Sketch the following polynomial: \(y=(2x+1)^2(x-1)^2\) labelling all \(x\) and \(y\) intercepts.
2. Sketch the following polynomial: \(y=x^2(2x-3)^3\) labelling all \(x\) and \(y\) intercepts.
3. Sketch the following polynomial: \(y=(3x+1)^3(x+1)(x-1)^2\) labelling all \(x\) and \(y\) intercepts.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
