Part 2: Absolute Values | Further Functions and Relations

In this article, you will learn how to sketch absolute value graphs and solve simple equations involving absolute values.

As you know, absolute values ensure that you always get a positive number. However, when we apply this concept with negative graphs, we need to examine what it looks like when it turns positive!

In this article, we’ll discuss

• The NESA Syllabus Outcomes
• Absolute values
• Graphs involving absolute values
• Piecewise definition of absolute values
• Equations involving absolute values
• Concept check questions

Year 11 Advanced Mathematics: Absolute Values

We want to explore the role of an Absolute Value in Mathematics, and how it affects the way we sketch our graphs. This guide will aim to break down the sketching of Absolute Values into a couple of simple steps which will hopefully make it easy to understand!

We’re going to be looking at the following syllabus points.

NESA Syllabus Outcomes

NESA dictates that students need to learn the following concepts to demonstrate proficiency in Absolute Values

F1.4 Further functions and relations – Absolute Values

• Define the absolute value \(|x|\) of a real number \(x\) as the distance of the number from the origin on a number line without regard to its sign
• Use and apply the notation \(|x|\) for the absolute value of the real number \(x\) and the graph of \(y=|x|\) (ACMSM098)
• Recognise the shape and features of the graph of \(y=|ax+b|\) and hence sketch the graph
• Solve simple absolute value equations of the form \(|ax+b|=k\) both algebraically and graphically

Assumed Knowledge

Students should be familiar with solving simple equations and have a deep understanding of how a piecewise function is defined.

There are not one but multiple ways on how we can approach sketching of functions involving absolute values. Therefore, knowing how to perform graphical transformations before going through this post would be extremely helpful.

Students can refresh their knowledge of simple equations in our Year 9 Guide article: Algebraic techniques.

Now lets’ have a closer look at what absolute values are.

The Beginner’s Guide to Year 11 Further Functions and Relations:  Absolute Values

Absolute Values

Absolute value, or modulus, tells you how far away a number is from \(0\) on the number line. It is represented by a double vertical bar.

It tells you the ‘distance’ from that number to \(0\) on the number line – and of course distance is always positive!

Let’s have a look at some simple examples:

\(|5|\) tells you how far away \(5\) is from \(0\) on the number line – which is \(5\) units.

Well then, what about \(|-5|\)?

Since \(-5\) is still \(5\) units away from \(0\) on the number line, we can also say that \(|-5| = 5\)

In short, you can ignore the sign of the number in the absolute value and you can say that everything that comes out from an absolute value will be positive.

Graphs involving Absolute Values

Of course, Maths is not always so simple – so we will now extend our concept of absolute values to functions.

The question is – how do we visualise an Absolute Value?

Example 1:

Let’s say you are given a function \(y=x+2\); let’s sketch this on our \(x/y\) axis.

Here is what it should look like:

We can see that to the right of \(x=-2\), every single \(y\)-value is positive as the graph is always above the \(x\)-axis.

On the other hand, the section of the graph to the left of \(x=-2\) is below the \(x\)-axis which means the \(y\)-value is negative.

To plot this, you need the two intercepts first – which should be \((-2,0)\) as \(x\)-intercept and \((0,2)\) as \(y\)-intercept.

Example 2:

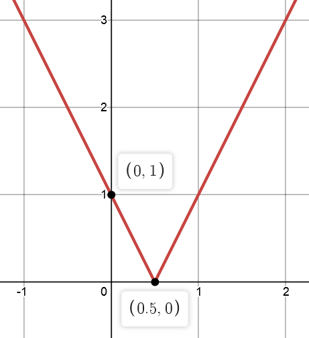
Now, let’s say you’re asked to sketch \(y=|x+2|\), what would be the first thing that we think about? Well, let’s recall that the absolute value turns any negative number into a positive number.

This means the section of the graph which is below the \(x\)-axis has to just be reflected upwards about the \(x\)-axis, essentially removing the negative signs from the \(y\)-values.

Hence, the graph will now look like this:

In summary, the best way to sketch an absolute graph is to sketch its original function as is in dotted line and reflect anything below the \(x\)-axis upwards and trace your solution as a solid line.

Example 3:

Let’s have a comparison between two graphs: \(y=x^2-2\) (in Blue) and \(y=|x^2-2|\) (in Red)

First, we sketch the original function of \(y=x^2-2\) as a dotted line, and then reflect the curve which lies below the \(x\)-axis upward to obtain the absolute graph.

How about the following function? Let’s try to think about how you would sketch this? It will no longer be as simple as what we have done so far!

Example 4:

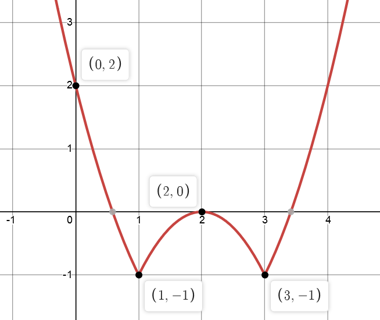
Sketch \(|(x-1)^2-3|+4\)

Consider the following process that we have broken down into 5 steps for sketching the above absolute value:

Piecewise Definition of Absolute Values

We have learnt about piecewise (or piecemeal) function when we studied functions and relations. A piecewise function describes a function that is built in different pieces over fragmented domains.

Example:

Let us consider a simple function \(y=|x-2|\) on an \(x-y\) axis.

From the graph, we can make two observations:

1. This graph is ‘broken’ into two straight lines at \(x=2\). Let’s call this point a ‘cusp’ of the absolute graph as it is a sharp point where you have reflected the curve about the \(x\)-axis.
2. The profile of both branches of this graph still remain as a straight line. After all, we have only reflected the original straight-line graph.

You can now see that we can describe this function over two separate domains. The first domain is for when \(x<2\) and the second domain is for when \(x≥2\).

Solution:

Now think about the original curve and which of these branches describe the ‘original’ function – that is \(y=x-2\)?

That’s right! It is indeed the right-hand branch of this graph. This means that we can describe this function as \(y=x-2\) for \(x≥2\).

The left-hand branch, on the other hand, is the ‘reflected’ curve of \(x-2\). When we reflected a graph, their \(y\)-values were changed from negative to positive.

This essentially means we have sketched \(y=-(x-2)\) on the left hand branch. We can describe this function as \(y=-x+2\) for \(x<2\)

With this information, we can write this absolute graph as a piecewise function as

$$
f(x) =
\begin{cases}
-x+2 & ;x>2 \\
x-2 & ;x<2
\end{cases}
$$

Equations Involving Absolute Values

Solving equations involving absolute values become trivial if you fully understand the meaning behind the concept.

Let’s consider a simple equation

By definition, \(x\) can be any number that is \(5\) units away from \(0\) on the number line. Therefore \(x\) can be either \(-5\) or \(5\), since both numbers are \(5\) units away from the origin on the number line.

Now consider a more complicated example.

Example:

\(|2x-1|=5\)
By definition, \(2x-1\) can be \(5\), or \(-5\). Now we can continue solving equations for both cases.

Solution:

\(2x-1=5\)
\(x=3\)
\(2x-1= -5\)
\(x=-2\)

From the two cases, we can conclude that \(x\) can take two values – either \(3\) or \(-2\).
It’s a good practice to always check your answers if they satisfy the equation too. In this case, both solutions satisfy the equation \(|2x-1|=5\)

Want to see an absolute improvement in your Year 11 Maths Adv marks?

Learn from The HSC Experts with our Year 11 Maths Adv course. Learn more.

Concept Check Questions

1. Evaluate \(|-7(2)+3|\)
2. Sketch the graph of \(y=|2x-1|\) Label all important features
3. Sketch the graph of \(y=|(x-2)^2-3|-4\)
4. Express \(f(x)=|x-5|\) as a piecewise function
5. Express \(f(x)=-|5-x|\) as a piecewise function
6. Express \(f(x)=|2x+4|-3\) as a piecewise function
7. Solve \(|2x-5|=35\)
8. Solve \(|x+2|-5=10\)

Answers

1. 11
2. 
3. 
4. $$
   f(x) =
   \begin{cases}
   5-x & ;x<5 \\
   x-5 & ;x\geq5
   \end{cases}
   $$
5. $$
   f(x) =
   \begin{cases}
   x-5 & ;x<5 \\
   5-x & ;x\geq5
   \end{cases}
   $$
6. $$
   f(x) =
   \begin{cases}
   -2x-7 & ;x<-2 \\
   2x+1 & ;x\geq-2
   \end{cases}
   $$
7. \(2x-5=35 \) or \(2x-5= -35\)
   \(∴x=20\) or \(-15\)
8. \(|x+2|-5=10\)
   \(|x+2|=15\)
   \(x+2=15\) or \(x+2=-15\)
   \(x=13\) or \(-17\)