Do you struggle wrapping your head around functional mapping? You’re not alone! In this article, we will be introducing the concepts you need to understand to ace further functions and relations for Year 11 Maths Advanced.
This post will be dedicated to the study of functions, their properties and how they interact when subjected to a range of operations.
Understanding relations and functions play a crucial role in many Year 11/12 topics.
It is extremely important for students to recognise the difference between relations and functions especially for future topics such as introductory calculus and curve sketching.
NESA has provided the following outcomes for this topic:
Students should be familiar with graphing basic curves and understanding their equations such as the straight lines, parabolas and circles.
Each point on these curves contain a \(x\) and \(y\) coordinate which we will be using in our introduction to relations and functions. Hence, familiarising yourself with a good understanding of graphs and curves is recommended before going through this post.
Students should also be familiar with working with the number line and sketching inequalities onto it.
A relation is a set of ordered pairs \((x,y)\) where \(x\) and \(y\) are real numbers.
“Ordered” pairs means that the order of the \(x\) and \(y\) coordinates matter, i.e. \((3,4)\) is different to \((4,3)\).
Example of relations:
We can use an arrow diagram to represent the relation of mapping one set of points to another set of points. To do this, we list the \(x\)-coordinates into the first set \(X\) and the \(y\)-coordinates into the second set \(Y\). Then we draw an arrow from \(x\) to \(y\) for each pair of \((x,y)\).
Consider the set of points \({(1,1),(1,5),(2,4),(3,3)}\) from our previous example. We can visualise this relation in the arrow diagram below.
This relation is known as a “one-to-many” relation since the first element of set \(X\), \(1\), is mapped to more than one element in set \(Y\), which are \(1\) and \(5\).
There are four types of relation mapping which we describe in the table below:
| Type of Mapping | Arrow Diagram Description |
| One-to-one |
Each element of set \(X\) is mapped to only one element of set \(Y\) Each element of set \(Y\) is mapped from at most one element of set \(X\) |
| Many-to-one |
All elements in set \(X\) are mapped to at most one element in set \(Y\). There exists an element in set \(Y\) which has more than one element mapped to it from set \(X\). |
| One-to-many |
There exists an element in set \(X\) which is mapped to more than one element in set \(Y\) All elements of set \(Y\) is mapped from at most one element of set \(X\) |
| Many-to-many |
There exists an element in set \(X\) which is mapped to more than one element in set \(Y\). There exists an element in set \(Y\) which is mapped from more than one element of set \(X\). |
A function is a set of ordered pair \((x,y)\) where every pair has a unique \(x\) component. This means a function is a relation between two variables where each value of \(x\) has only one corresponding value for \(y\). Hence, a function can be a “one-to-one” or “many-to-one” relation however, not all relations are functions.
We can determine whether a relation is a function by drawing vertical lines on the graph of its curve.
Example:
Let’s investigate the relations \(x^2+y^2=1\) and \(y=x^2-1\) to determine whether they are functions.
Solution:
First, we can draw both curves as shown below.
Draw any vertical line, say \(x=0.5\), through the graphs of the curves.
The vertical line intersects the circle at two points whereas it will only intersect the parabola at one point. Therefore, we can say the circle \(x^2+y^2=1\) is not a function and the parabola \(y=x^2-1\) is a function because there can only be one point of intersection for the vertical line test.
Now that we understand what functions are, we can use a special notation to represent them, called function notation. A function can be perceived as a machine that takes inputs and converts it into another form as an output.
Consider the function from our previous example \(y=x^2-1\).
We know that functions use a set of numbers as input (\(x\)-values) and outputs another set of numbers (\(y\)-values). Now we just need a method to write these sets of numbers.
Interval notation is an easy way of expressing parts of the real number line without having to use variables \(x\) and \(y\).
Let’s examine the inequality \(-2<x\leq2\), which is shown on the number line below:
To write an interval using interval notation, we use two types of brackets to note the difference between open circles and closed circles.
We know that number lines go on forever, so we also need a method to write intervals that go on forever. In interval notation, we can express this using the infinity symbol \(\pm\infty\)
Consider the inequality \(x\geq 5\), shown on the number line below:
This interval can be written as \([5,\infty)\).
Note that, we write the infinity symbol with a round bracket and not a square bracket because infinity is not an actual number and hence, we cannot include it on the number line.
We can also combine multiple intervals using the union symbol \(\cup\).
Consider the previous two inequalities \(x\geq5\), \(-2<x\leq2\).
If we want to express the combination (union) of both these intervals together, we can write it as \((-2,2] \cup [5,\infty)\). This is shown on the number line below:
The set of values that may be assigned to the independent variable \(x\) is called the domain. It tells us the possible \(x\)-values the relation or function can take.
The set of values that the dependent variable \(y\) can take is called the range which corresponds to the \(y\)-values.
When writing your solutions, you must state whether you are finding the domain \((D)\) or range \((R)\).
Let us consider the parabola from our previous example \(y=x^2-1\).
By looking at all the \(x\)-values the parabola can take, we can write the domain as \(D=(-\infty,\infty)\).
Similarly, by looking at all the possible y-values, we can write the range as \(R=[-1,\infty)\).
A function \(f(x)\) is called an even function if \(f(-x)= f(x)\). The graph of an even function is symmetrical about the \(y\)-axis.
Example:
Show that the function \(f(x)=x^2-1\) is even.
Solution:
To show that a function is even, we need to show that \(f(-x)= f(x)\).
\begin{align*}
f(-x)&=(-x)^2-1 \\
&=x^2-1 \\
&=f(x)
\end{align*}
So, \(f(-x)= f(x)\) and the function \(f(x)=x^2-1\) is even.
A function \(f(x)\) is called an odd function if \(f(-x)= -f(x)\). The graph of an odd function has 180 degrees point of symmetry about the origin i.e. if you spin your page \(180\) degrees about the origin, the graph will look the same.
Example:
Show that the function \(f(x)=x^3\) is odd.
Solution:
To show that a function is even, we need to show that \(f(-x)= -f(x)\).
\begin{align*}
f(-x)&=(-x)^3 \\
&=-x^3 \\
&=-f(x)
\end{align*}
So, \(f(-x)= -f(x)\) and the function \(f(x)=x^3\) is odd.
1. Determine the mapping type for the following sets:
(a) The set of points \({(1,4),(2,4),(3,5)}\).
(b) The set of points \({(a,1),(b,3),(c,3),(c,5)}\) where \(a\),\(b\) and \(c\) are real numbers.
(c) The set of points that satisfy the equation \(y=x+1\).
(d) The set of points that satisfy the equation \(y=x^2-1\).
2. Given that \(f(x)=x^2-3x+4\):
(a) Evaluate \(f(2)\).
(b) Evaluate \(f(-2)\).
(c) Evaluate \(f(3)-f(1)\).
(d) Find \(f(x+1)-f(x)\).
3. Express the following intervals using interval notation:
(a) \(-1<x<0\).
(b) \(5\leq \ x<6\).
(c) \(x\leq4\).
(d) \(x<-2,3\leq \ x\leq6\).
4. Show that the function:
(a) \(f(x)=(x^2-3)^3\) is even.
(b) \(f(x)=x^3-2x\) is odd.
(c) \(f(x)=(x+1)^2\) is neither odd nor even.
1.
(a)
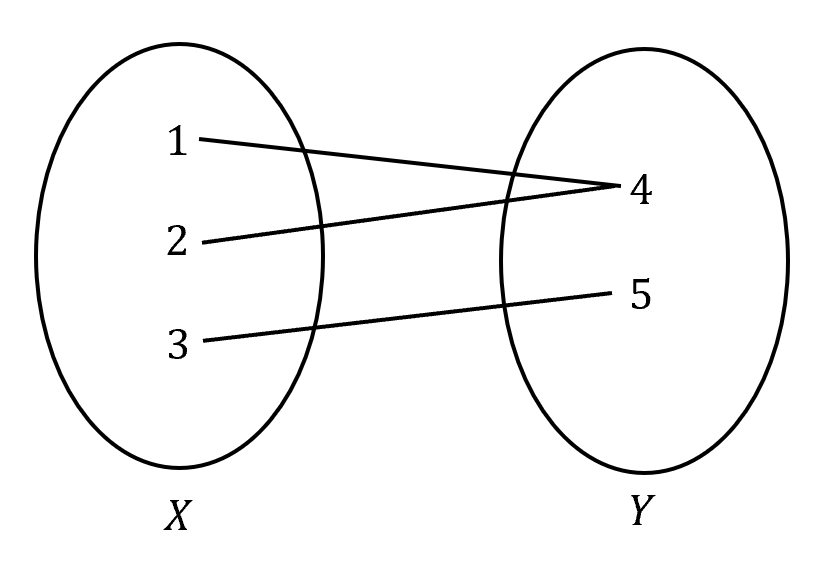
(b)
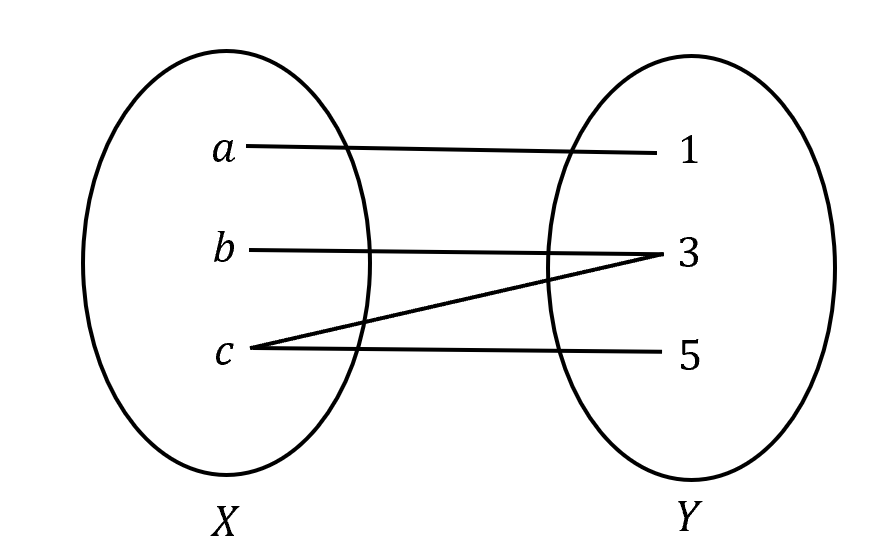
(c)
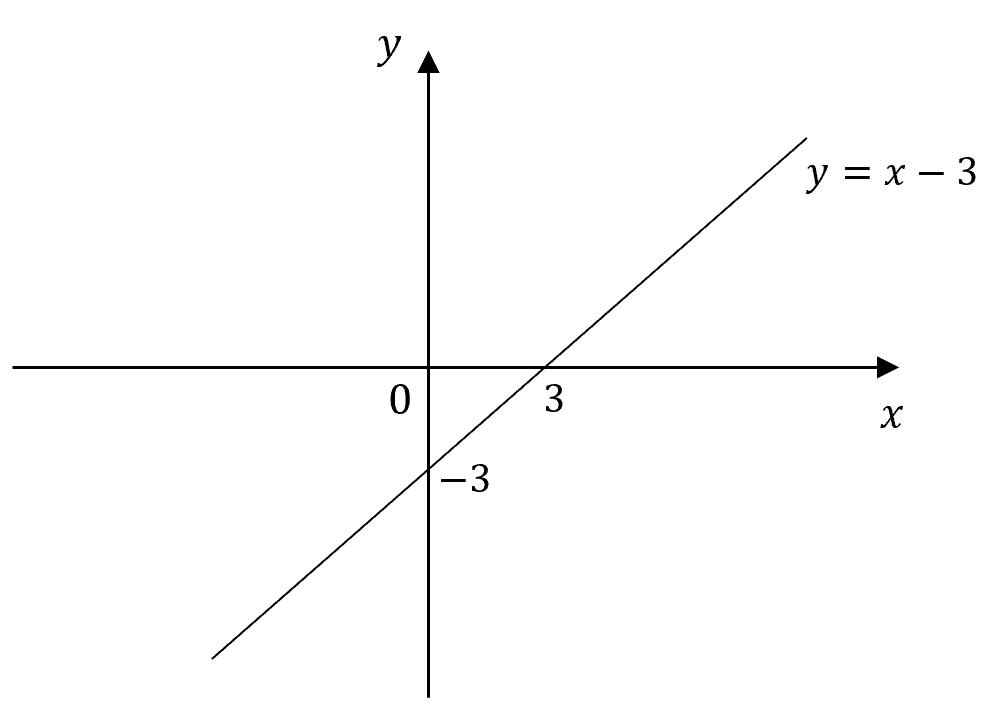
(d)
2.
(a)
\begin{align*}
f(2)&=2^2-3(2)+4\\
&=2\\
\end{align*}
(b)
\begin{align*}
f(-2)&=(-2)^2-3(-2)+4\\
&=14\\
\end{align*}
(c)
\begin{align*}
f(3)-f(1)&=[3^2-3(3)+4]-[1^2-3(1)+4]\\
&=4-2\\
&=2\\
\end{align*}
(d)
\begin{align*}
f(x+1)-f(x)&=[(x+1)^2-3(x+1)+4]-[x^2-3x+4]\\
&=[x^2+2x+1-3x-3+4]-[x^2-3x+4]\\
&=[x^2-x+2]-[x^2-3x+4]\\
&=2x-2\\
\end{align*}
3.
(a) \((-1,0)\)
(b) \([5,6)\)
(c) \((-\infty,4]\)
(d) \((-\infty,-2) \cup [3,6]\)
4.
(a)
\begin{align*}
f(-x)&=[(-x)^2-3]^3\\
&=(x^2-3)^3\\
&=f(x)\\
\end{align*}
So, \(f(-x)= f(x)\) and the function is even.
(b)
\begin{align*}
f(-x)&=(-x)^3-2(-x)\\
&=-x^3+2x=-(x^3-2x)\\
&=-f(x)\\
\end{align*}
So, \(f(-x)= -f(x)\) and the function is odd.
(c)
| \begin{align*} f(-x)&=(-x+1)^2\\ &=(-1)^2 (x-1)^2\\ &=(x-1)^2\\ \end{align*} |
We observe that \(f(-x)\neq f(x)\) and \(f(-x)\neq -f(x)\), hence the function is neither odd nor even.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
