Part 1: Year 9 Algebraic Techniques and Equations | Free Worksheet

Year 9 Algebraic Techniques and Equations

Mastering Algebraic Techniques in Year 9 is crucial to successfully navigate through senior mathematics and secure your fundamentals. Here are some tips that you must know before moving on to Year 10.

NSW Syllabus Outcome

This article deals with the following NESA Syllabus Outcomes:

In this article we’ll discuss:

• Optimising BODMAS Equations (with fractions!)
• Expanding Binomial Products
• Factorising Quadratics to Binomial Products
• Tackling Word Equations

Assumed knowledge

Students should understand basic equation solving and algebra. This guide aims to enrich these skills with techniques and advice from our knowledgeable Matrix Mathematics Teachers and Tutors.

Solving Algebraic Equations (BODMAS)

The key to solving algebraic equations is a matter of following a few simple rules. These rules are not necessarily set in stone, but they can streamline the process of answering questions.

As you already know, BODMAS is the acronym for the order used to solve equations – Bracket, Of, Division, Multiplication, Addition and Subtraction.

1. Isolate the variable

This should be the end goal of any given question, but keeping it in mind can help you get there. To isolate a variable, make one variable the subject while moving all other variables to the other side of the equation.

For example, if the equation was:

\(10x + 2=22\)

We identify that the pronumeral \(x\) is on the left-hand side (LHS) of the equation, so we must move everything else to the other side. This starts by subtracting the 2 to the right-hand side (RHS).

So we have:

\(10x=20\)

Now the \(x\) term is isolated on the LHS, and the final step is to divide both sides by 10.

\(x=2\)

2. Remove any fractions

If there are fractions in the equation, they should be “undone”. This can be achieved by multiplying the entire equation by the lowest common multiple (LCM) of all the denominators.

For example:

\(\frac{k}{4} -\frac{k}{3}= 7\)

The denominators 4 and 3 would form the LCM of 12! So now we must multiply EVERY term in the equation by 12.

\begin{align*}
12 \Big{(} \frac{k}{4} \Big{)}-12 \Big{(} \frac{k}{3} \Big{)}=12(7) \\
3k-4k=84 \\
-k=84 \\
k=-84
\end{align*}

3. Expand any brackets

This will be explained in proper detail in the “Expanding Binomial Products” section of this guide. However, there are some cases where a faster method can be used: Rule 1!

\(6(3x+1)= 12\)

If we were to expand the brackets we would have to solve the following:

\(18x+6=12\)

But instead of expanding the brackets, we can use Rule 1 and try to isolate \(x\) by dividing 6 on both sides.

\(3x+1=2\)

Now this is a much simpler equation to solve.

4. Collect all the variables

Questions with multiple instances of the same variable require you to collect the variables onto one side of the equation. Again, we need to keep Rule 1 in mind, as we must isolate the variable once we have collected it.

For example, if the equation was:

\(3d – 8 = 5d + 4\)

Notice there are instances of variable \(d\) on both sides of the equation. We want collect them all onto the LHS. So, we have to subtract \(5d\) to both sides:

\(-2d – 8 = 4\)

Again, we should apply Rule 1 and isolate the variable:

\(-2d = 12\)
\(d = -6\)

Once you get comfortable with these type of questions, you can solve them faster by “moving terms around” through inverse operations.

Expanding Binomial Products

Binomials are simply two terms which add or subtract from each other, like:

\(x-2\) or \(a+b\)

When these binomials are multiplied by each other, we have a binomial product. This is not as easy as using the multiplication table!

Luckily we have an important arithmetic law known as the distributive law which shows us how to expand expressions with brackets.

Consider the example below:

In this example, “a” is being distributed to each term within the second bracket. “b” is similarly distributed afterwards.

Consider this example

Common Mistakes

• Forgetting to multiply across the negative
• Forgetting to simplify the expression after expansion
• Not changing the sign when two negatives are multiplied

Factorising Quadratics

Similarly, we can go backwards from an expanded quadratic like \(x^2-4x+3\) to a binomial product by factorising. Being able to do this confidently will be important before moving onto Year 10.

Here is an example:

\(x^{2}+5x+6=(x+3)(x+2)\)

You can verify that this is true by expanding the RHS.

The factorisation process can be explained by examining the constant terms on the RHS: 3 and 2. Now,

• When these constants are multiplied, the result is 6
• When they are added, the result is 5

This matches with what we see on the LHS.

Here is another example:

\(x^{2}+x-12=(x+4)(x-3)\)

The constant terms from the brackets are 4 and -3. Now,

• \(4×(-3)=-12 \) and \(-12\) is the constant term on the LHS
• \(4+(-3)= 1 \) and 1 is the coefficient of x on the LHS

Thus, to factorise any quadratic in the form \(x^{2}+bx+c\):

Find two numbers whose product equals \(c\), and whose sum equals \(b\).

This can be tracked by using what is known as the cross method, which is demonstrated below.

Cross method

Factorise \(x^{2}+5x+4\)

\(x^{2}+5x+4\)

Explanation

Find the two factors of \(2x\) and write them as shown.

Next, find two numbers that multiply to give \(4\).

Next, multiply across the diagonals to get the terms \(2x\) and \(2x\).

Then add these two terms:

\(2x + 2x = 4x\)

Since this does not match with \(5x\) the the two numbers are not correct.

Try two different numbers.

Factorise \(x^{2}+5x+4\)

\(x^{2}+5x+4\)

Therefore \( x^{2}+5x+4 = (x+4) (x+1)\)

Explanation

Using the cross method again,

Therefore, these two numbers are the ones you want, and now you’re ready to factorise.

To factorise, read the cross horizontally:

\( \color{Orange}{x \rightarrow 4 }\)
\( \color{DarkGreen}{x \rightarrow 1} \)

Reading off the cross,

Common Mistakes

• Not applying simple factorisations first e.g.
  \(3x^2-3x-36=3(x^2-x-12)\)
  \(=3(x-4)(x+3)\)
• Forgetting to factorise out the negative from an equation (when applicable).

Solving Problems Using Algebra

In the real world, equations can be applied to solve practical problems. These problems won’t be given simply as “find \(x\)”, but instead we have to be able to interpret and solve worded problems.

Common types of word problems can include number, measurement, money, or age problems.

To solve these problems, we must convert the problem into equations that can be solved algebraically:

1. Read the problem carefully and underline the key information.
2. Let x be the unknown quantity. Usually we choose the value that we are finding.
3. Translate the word problem into an algebraic equation.
4. Solve the equation.
5. Answer the question in words.

Example: Number Problem

The sum of two numbers is 24. When the larger number is subtracted from 4 times the smaller number, the result is 16. Find the two numbers.

Solution

First, we must define our unknown. Since we are trying to find the two numbers, let us make \( \color{DarkGreen}{x}\) the smaller number.

From the question, we also know that the sum of the two numbers is 24.

Hence, the larger number must be \(\color{orange}{24-x}\).

Translating “When the larger number is subtracted from 4 times the smaller number, the result is 16” into mathematical form, we get:

\(4×\color{DarkGreen}{smaller \ number}-\color{Orange}{larger \ number}=16\)

Now we can substitute the unknown values that we just defined to form an algebraic equation:

\(4×\color{DarkGreen}{x}-\color{orange}{(24-x)}=16\)

At this point, we can simply solve for x.

\(4x-24+x=16\)
\(5x=40\)
\(x=8\)

Using our definition of \(x\), we know that the smaller number is 8. Therefore, the larger number must be \(24-8=16\).

Answering the original question in words:

The two numbers are 8 and 16.

Example: Measurement Problem

The length of a rectangular house block is 15 metres greater than twice its street width. A fence around the perimeter of the block, except for the side facing the street is 80 metres long. Find the dimensions of the block.

Solution

Let us make the width \(\color{DarkGreen}{w}\) metres. Since the length of the block is 15 metres greater than twice the width, the length can be written as \(\color{Orange}{2w+15}\) metres.

Now that we have defined our unknowns, we can draw a diagram to illustrate the question:

From the question, we know that the combined length of three fenced sides is 80 metres. This can be translated mathematically as:

\(2×\color{Orange}{length}+\color{DarkGreen}{width}=80\)

Substituting in the values we have defined, we get an algebraic equation:

\(2×\color{Orange}{(2w+15)}+\color{DarkGreen}{w}=80\)

At this point, we can solve for w.

\(4w+30+w=80\)
\(5w=50\)
\(w=10\)

Hence the width of the block is 10 metres. Therefore, the length must be \(2×10+15=35\) metres.

Finally, we must answer the original question:

The block is 10 metres wide and 35 metres long.

Example: Age Problem

3 years ago, John was twice Ryan’s age. Now, the sum of their ages is 36.

How old are they now?

Solution

In age problems, the best thing to do is to draw up a table, with columns and rows representing each person and time period give in the question.

We will let one of the cells be x, in this case it will be John’s age 3 years ago.

We can now fill out the rest of the table, in terms of \(x\). For example, Ryan’s age 3 years ago will be \(2x\), as given by the question. Afterwards, we can fill in the “Now” row, just by adding 3 to each expression (since it is 3 years later). So our table looks like this.

Finally, we can use the final part of the question to create an equation to solve. We know the sum of their ages now is 36, so we have:

\begin{align*}
x + 3 + 2x + 3 = & \ 36 \\
3x = & \ 30 \\
x =  & \ 10
\end{align*}

Now we have the value for x, so we can find the value for each of their ages. John’s present age is \(x+3\), so his age is now 13. Similarly, Ryan’s age is \(2x+3\), so his age now is 23.

Final answer:

John is 13 and Ryan is 23

Common mistakes

Common mistakes students make in problem-solving questions are:

• Forgetting to use brackets when substituting in the unknown values
• Forgetting to answer the original question in words.

Checkpoint Questions

1. Expand and simplify the following

\(3(2x+1)-1\)

2. Factorise the expression below

\(x^{2}-5x+6\)

3. Expand and simplify the following

\((2x-1)(x+3)\)

4. The area of a rectangle is \(10cm^{2}\). What are the dimensions of the rectangle if the length is 3cm longer than the width? (Note: Let \(w\) be the width of the rectangle)

5.Factorise the following

\(6x^{2}-12x+6\)

6. Expand and simplify the following

\(3((x-2)^{2}-1)÷(x-1)\)

7. Sam’s brother is 3 years older than twice his sister’s age.  If the product of Sam’s brother’s and sister’s ages is 65. What is Sam’s brother’s age?

8. Expand the following then factorise.

\((x+x^{-1} )(x+3)-\frac{3}{x}+1\)

9. 4 years ago, Andy’s age was 5 less than twice Jessica’s. In 2 years from now, the sum of their ages will be 25. How old are they currently?

10. Given that \(c=\frac{a}{b}\), prove that:

\(\frac{a}{(a+b)}+\frac{a}{(b-a)}=\frac{2c}{(1-c^2 )}\)

Solutions

1.

\(6x+3-1=6x+2\)

2. We need to find to numbers that multiply to be 6 and sum to -5. From cross method, we see the numbers are -2 and -3. Hence the factorised form is

\((x-2)(x-3)\)

3.

\((2x-1)(x+3)=2x^{2}+(2x)(3)-x-3\)
\(=2x^{2}+5x-3\)

4. Note the length will be \(w+3\). The area is hence \(w(w+3)\). From the question:

\(w(w+3)=10\)
\(w^{2}+3w-10=0\)
\((w-2)(w+5)=0\)
\(w=2\) or \(w=-5\)
Since \(w>0\), \(w=2\) only.
So the dimensions of the rectangle is \(w=2\) and \(l=5\)

5. Using the cross method,

\(6x^{2}-12x+6=6(x^{2}-2x+1)\)

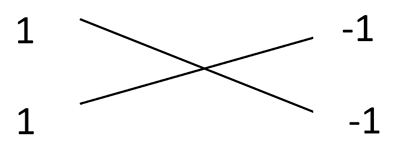
Hence the solution is \(6(x-1)^{2}\)

6. Converting the division symbol into a fraction and expanding the perfect square we get

\(\frac{3((x^{2}-4x+4)-1)}{(x-1)}\)
\(=\frac{3(x^2-4x+3)}{(x-1)}\)
\(=\frac{3(x-3)(x-1)}{(x-1)}\)
\(=3(x-3)\)

By cancelling \(x-1\).

7. Let Sam’s sister’s age be \(s\), so then Sam’s brother’s age is \(2s+3\). Since the product of their ages is 65, this must mean:

\(s(2s+3)=65 \)
\(2s^{2}+3s-65=0 \)
\((2s+13)(s-5)=0 \)
\(s=-\frac{13}{2} \  \text{or} \ s=5\)

Since \(s\geq0\) (ages are positive), \(s=5\).

8. Remember from index laws, \(x^{-1}=\frac{1}{x}\)

\begin{align*}
(x+x^{-1} )(x+3)-\frac{3}{x}+1 \\
=x^{2}+3x+\frac{x}{x}+\frac{3}{x}-\frac{3}{x}+1 \\
=x^{2}+3x+1+1 \\
=x^{2}+3x+2 \\
=(x+2)(x+1) \\
\end{align*}

9. By letting Jessica’s age 4 years ago be \(x\), we can work out that Andy’s age was \(2x-5\) then. We proceed to add 4 and 6 to get their ages now and 2 years later respectively.

We are told that the sum of their ages 2 years later is 25. So,

\(2x+1+x+6=25\)
\(3x+7=25\)
\(x=6\)

Therefore their current ages (now) is obtained by substituting \(x=6\).

Andy is 11 and Jessica is 10

10.

\begin{align*}
LHS=\frac{a}{a+b}+\frac{a}{b-a} \\
=\frac{(a(b-a)+a(a+b))}{b^{2}-a^{2}} \\
=\frac{ab-a^{2}+a^{2}+ab}{b^{2}-a^{2}} \\
=\frac{2ab}{b^{2}-a^{2}}                             (*) \\
\end{align*}

Recall \(c=\frac{a}{b}\), so \(a=bc\)

\begin{align*}
=\frac{2(bc)b}{b^{2}-(bc)^{2}} \\
=\frac{2b^{2} c}{b^{2}-b^{2} c^{2}} \\
=\frac{2c}{1-c^{2}} \\
\end{align*}
(Note you can also divide top and bottom of (*) by \(b^{2}\) to get the answer immediately however this is slightly unnatural)

Additional Challenging Examples (From the Year 9 Maths MAX Series)

Questions

Solutions

Need more practice questions?

Be more prepared for your next ‘Algebraic Techniques’ exam with Year 9 Max Series Exam Preparation Book.