Year 9 Maths
Year 9 Maths tutoring at Matrix is known for helping students build a solid foundation.
Learning methods available
Select a year to see available courses

Being able to determine the volume of composite solids is an essential skill that is necessary for several Year 11 and Year 12 topics such as optimisation. It is important that you understand the meaning of each term in the volume formulas now because it will be useful in the long run. This will become assumed knowledge in the years ahead!
This article addresses the following syllabus outcomes:
These Outcomes will, like Surface Areas, equip you to be able to evaluate the volumes of real-world objects so you can discuss them accurately.
In addition, to the cylinders, cones, and spheres we looked at in the previous article, we shall also be looking at how to calculate the volume of prisms.
Students should be familiar with the conversion between units of volume as well as conversion between units of length:

Knowledge of how to determine the area of composite shapes that may be broken down into special quadrilaterals, triangles and circles/semicircles will also be required.
A prism is defined as a solid geometric figure that has the same plane shape for its cross-sectional face across its entire height. Examples of prisms are shown below:
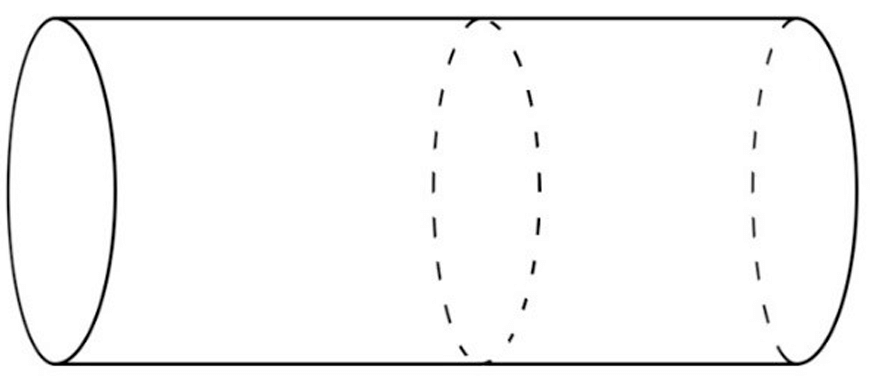
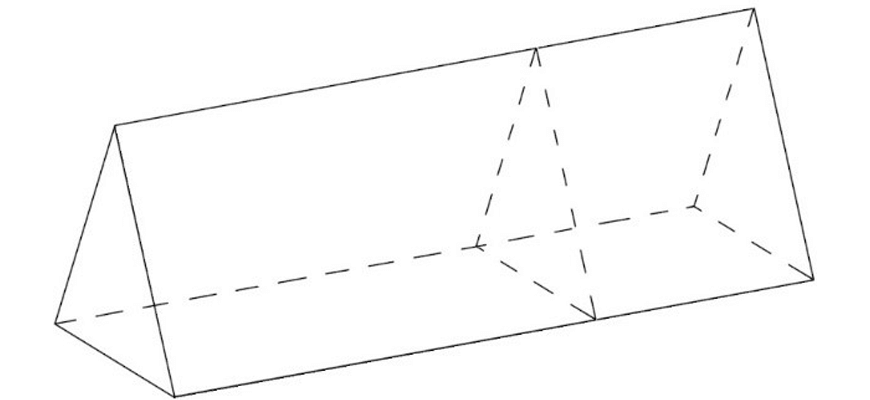
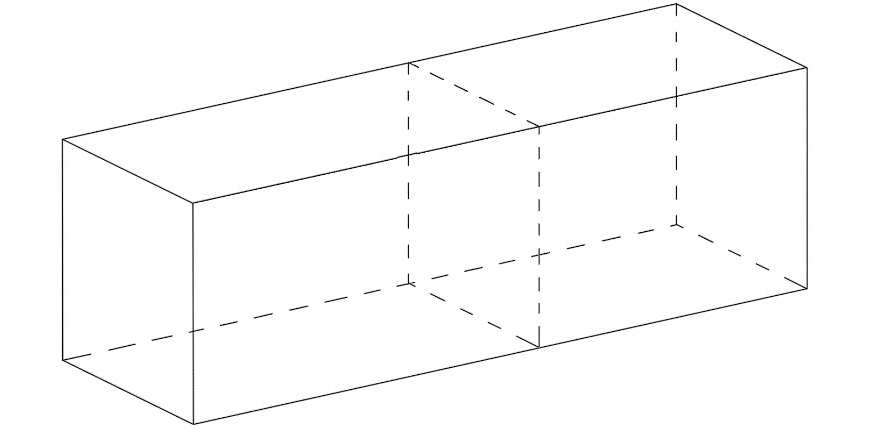
When we need to determine the volume of a prism, we use the formula:
\(V_{\text{prism}} = A_{\text{base}} \times h\)Where:
For the three prisms shown above, their bases have been shaded-in and their heights have been marked below.
Note that the base of the prism is the side which has a plane shape that is congruent to any cross sections taken in the same direction:
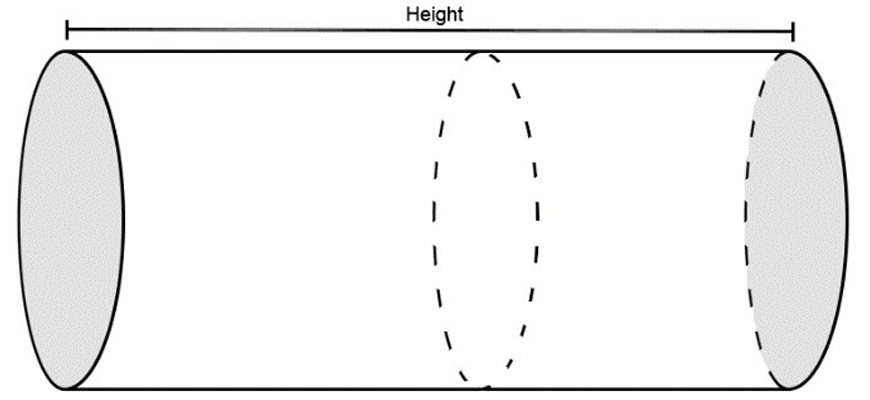
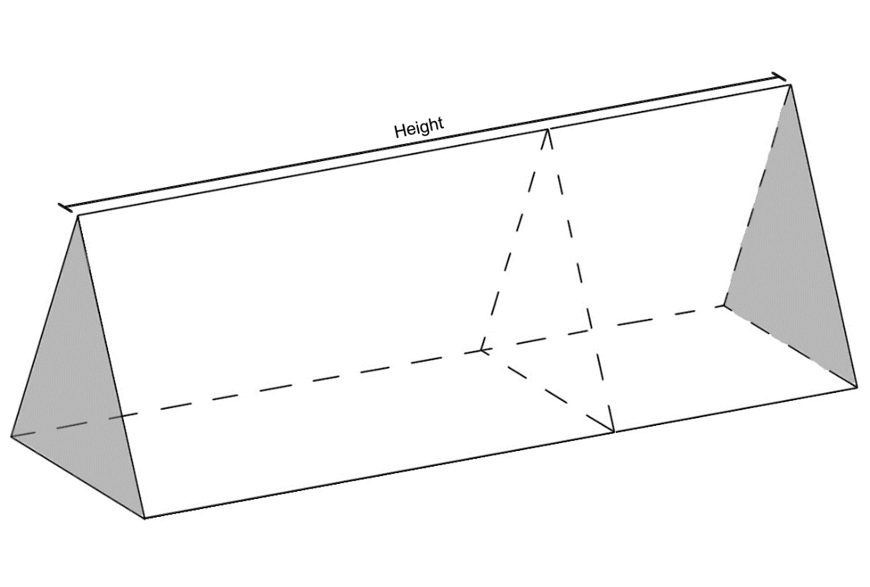
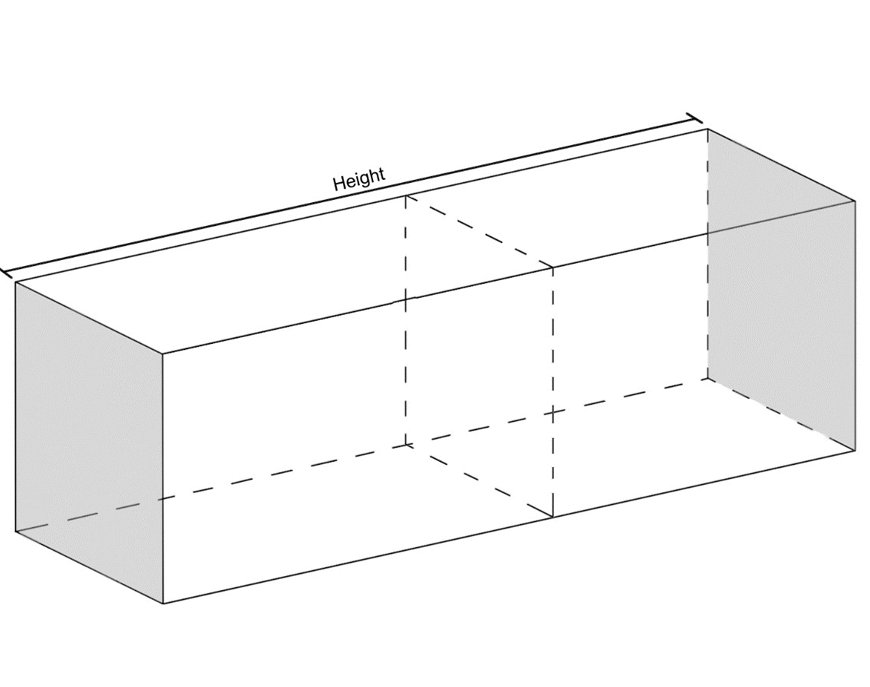
Notice how the area of this prism’s base is identical to the area of its uniform cross section.
Determine the volume of the trapezoidal prism below. The diagram is not to scale:
To find the volume of this solid, we must first determine the area of the base of the prism. In this question, the base is a trapezium (as shown below):
Therefore,
\(A_{\text{base}} = \frac{1}{2}(4+10) \times = 42 m^{2}\)We then must multiply this value for \(A_{\text{base}}\) with the value for the height of the prism. In this question, the height is 500 cm (or 5 metres).
∴\(V_{\text{prism}}=A_{\text{base}} ×h=(42)(5)=210 m^3\)
Note to students:
Remember to convert all units of lengths in the question to a single unit so that you are only working with one!
A pyramid is defined as a solid geometric figure that has a polygon as its base, and triangles as it sides. These triangular sides meed at a singular point called the vertex.
A cone is a more general form of a pyramid which consists of a flat base (most commonly, but not necessarily, circular), which narrows to a singular point called the vertex.
To determine the volume of a cone or a pyramid, we use the exact same formula for both:
\(V_{\text{cone / pyramid}}=\frac{1}{3}×A_{\text{base}} ×h\)Where:
The most common pyramids and cones you will come across are shown below. Their bases have been shaded in and their perpendicular heights marked.
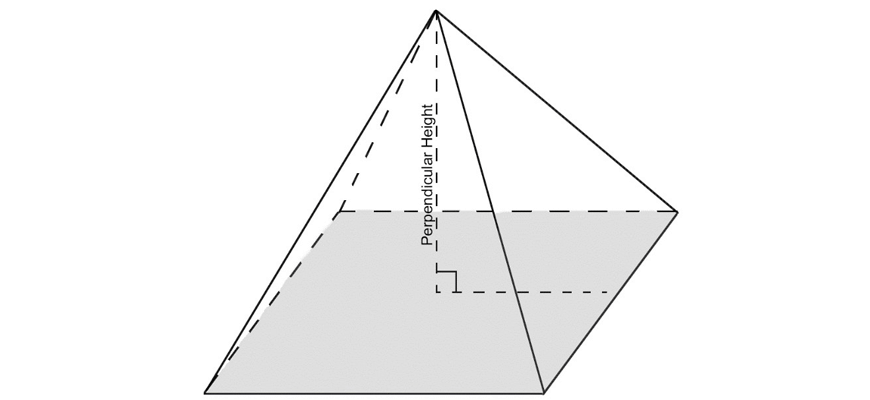
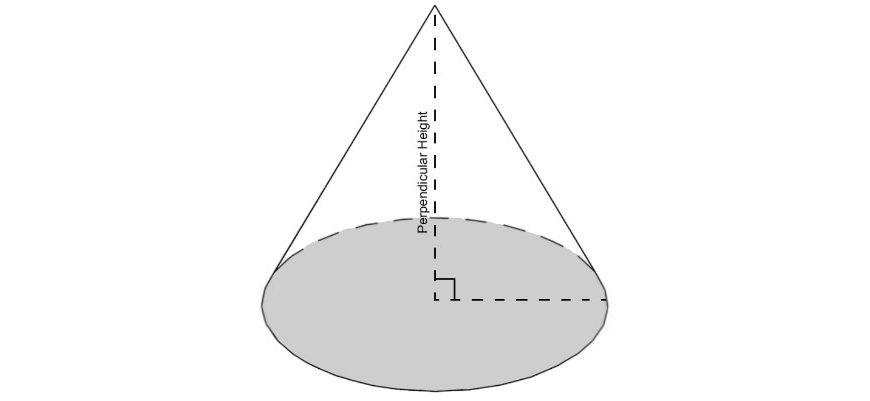
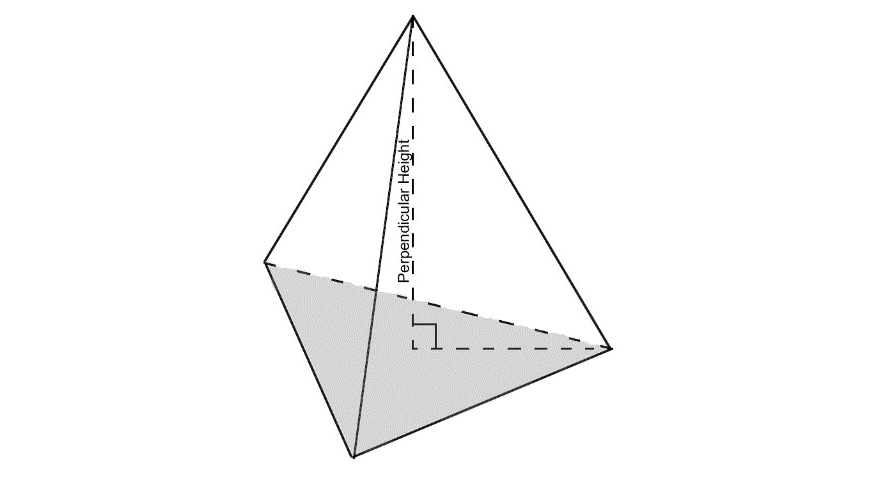
Note to students:
The perpendicular height will not always be given to you and you may need to use Pythagoras’ Theorem to calculate it!
Determine the volume of the square pyramid below. The diagram is not to scale
To determine the volume of this solid, we must first find the area of its base. As the base is a square, we know that its area is:
\(A_{\text{base}}=(6)(6)=36 m^2\)We must then find the perpendicular height of the pyramid.
In this question, we are only given the slant height. This slant height is the hypotenuse of the right angled triangle formed by the perpendicular height and half the base length.
So, we must use Pythagoras’ Theorem to determine the perpendicular height:
∴\(h= \sqrt{10^{2}-3^{2}} \text{(Using Pythagoras’ Theorem)}\\
=\sqrt{100-9}\\
=\sqrt{91} m \)
Hence, we can now determine the volume:
\(V=\frac{1}{3}×A_{\text{base}} ×h \\
A sphere is defined as a solid geometric figure where every point on its surface is equidistant to a singular point called the centre.
The distance between the centre and any point on the surface of the sphere is referred to as its radius.
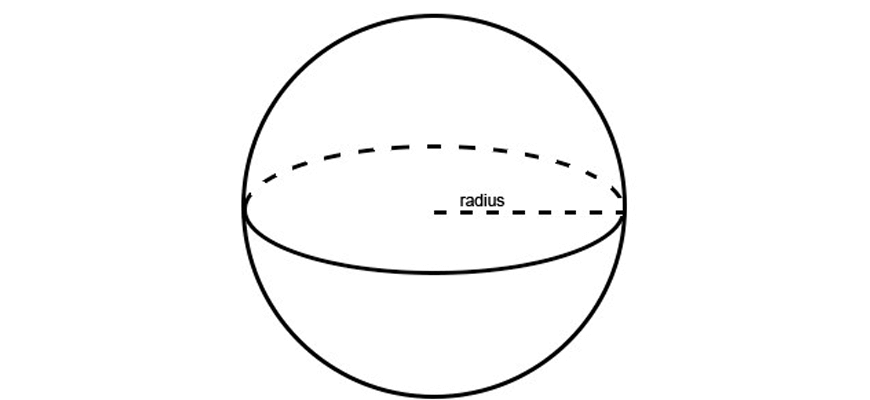
To find the volume of a sphere, we use the formula:
\(V_{\text{sphere}}=\frac{4}{3} \pi r^3\)Where:
Determine the volume of the hemisphere below. The diagram is not to scale
Solution:
To determine the volume of this solid, we must first find its radius.
In this question, we are given the diameter of the hemisphere as being 20 mm, meaning that its radius is 10 mm. We also know that a hemisphere has half the volume of its corresponding sphere.
Hence, we can find the volume with the equation:
\(V_{\text{hemisphere}}=\frac{1}{2} V_{\text{sphere}} \\
To determine the volume of a given solid, first determine whether it is a prism, pyramid, cone, sphere or a combination of them.
Then, find the required values (radius, height, area of the base etc.) to substitute into the given formulas to find the volume of the solid.
\(V_{\text{prism}}=A_{\text{base}} ×h\)
\(V_{\text{cone/pyramid}}=\frac{1}{3}×A_{\text{base}} ×h\)
\(V_{\text{sphere}}=\frac{4}{3} \pi r^3\)
Check your skills with the following challenging exercises.
1. Determine the volume of the triangular prism below:
2. Find the volume of the prism:
3. Determine the volume of the below solid:
4. What is the radius of a sphere with volume \(\frac{256}{3} \pi cm^3\)?
5. Determine the height of the composite solid below given that its volume is \(240 m^2\):
6. Find the volume of the below prism:
7. A builder wants to construct a garden feature made of cement. If the cost of cement is $50 per cubic metre, determine its cost:
8. Find the volume of the solid shown below:
9. Find the value of \(x\) given that the volume of this trapezoidal prism is \(264 m^3\)
10. Find the value \(r\) for given that the volume of this composite solid is \(36 \pi m^3\)
1. Using Pythagoras’ theorem to determine the height of the triangle:
\(
h_{\text{triangle}}=\sqrt{5^2-3^2} \\
=4 m \\
∴A_{\text{base}}=\frac{1}{2} bh_{\text{triangle}} \\
=\frac{1}{2} (6)(4) \\
=12 m^2 \\
∴V=A_{\text{base}}×h \\
=(12)(15) \\
=180 m^3 \\
\)
2. Determining the area of the prism’s base:
\(
A_{\text{base}}=A_{\text{semicircle}}+A_{\text{rectangle}} \\
=\frac{1}{2} \pi (3)^2+6×15 \\
=104.13 m^2 (\text{2d.p})\\
∴V=A_{\text{base}} \times h=(104.13…)(20)\\
=2082.74…m^3 \\
\)
3. The solid shown is a prism:
\(
A_{\text{base}}=A_{\text{large circle}}-A_{\text{smaller circle}} \\
= \pi (5)^2- \pi (3)^2 \\
=16 \pi m^2 \\
∴V=A_{\text{base}} \times h \\
=(16 \pi)(20) \\
=320 \pi \\
= 1005.31 m^3 (\text{2d.p}) \\
\)
4.
\(V_{\text{sphere}}=\frac{4}{3} \pi r^3 ≜\frac{256}{3} \pi \\
r^3=64 \\
∴r=4 \text{cm} \\
\)
5. The composite solid in this question is comprised of a triangular pyramid and a triangular prism. Let \(x\) be the height of the composite solid.
\begin{align*}
V_{\text{pyramid}}= & \ \frac{1}{3} × A_{\text{base}} × h \\
= & \ \frac{1}{3} × [\frac{1}{2} (4)(5)] × (x) \\
= & \ \frac{10}{3}x \\
V_{\text{prism}}= & \ A_{\text{base}} ×h \\
= & \ \frac{1}{2} (5)(x) × 15 \\
= & \ \frac{75}{2}x \\
∵V_{\text{solid}}= & \ 240 \\
\frac{75}{2} x+ \frac{10}{3} x= & \ 240 \\
\frac {245}{6} x = & \ 240 \\
x= & \ \frac{288}{49} \\
= & \ 5.87 m (\text{2d.p.})\\
\end{align*}
6.
\(
A_{\text{base}}=A_{\text{triangle}}+A_{\text{trapezium}} \\
=\frac{1}{2} (4)(8)+ \frac{1}{2} (8+5)(3) \\
=\frac{71}{2} m^2 \\
∴V=A_base×h \\
=(71/2)(14) \\
=497 m^3 \\
\)
7.
\(
A_{\text{base}}=(4.2)(2.3)-(1)(1.3) \\
=8.36 m^2 \\
∴V=A_{\text{base}} \times h \\
=(8.36)(1.5) \\
=12.54 m^3 \\
∴ \text{Cost}=(12.54)×50 \\
=$627
\)
8. The solid shown is a prism:
\(
A_{\text{base}}=A_{\text{rectangle}}-A_{\text{trapezium}} \\
=(12)(10)-\frac{1}{2} (5+12)(4) \\
=86 m^2 \\
∴V=A_{\text{base}} \times h \\
=(86)(35) \\
=3010 m^3 \\
\)
9.
\(
A_{\text{base}}=\frac{1}{2} (x+8)(4) \\
=2(x+8) \\
=(2x+16) m^2 \\
V=A_{\text{base}} \times h \\
=(2x+16)(11)≜264 \\
∴2x+16=24 \\
2x=8 \\
x=4 m \\
\)
10. The composite solid is comprise of a cone and a cylinder:
\(
V_{\text{solid}}=V_{\text{cone}}+V_{\text{cylinder}} \\
=\frac{1}{3} \times \pi r^2 (6)+ \pi r^2 (10) \\
=12 \pi r^2 \\
∵V_{\text{solid}}=36 \pi \\
∴12 \pi r^2=36 \pi \\
r^2=3 \\
r=\sqrt{3} m \\
\)
In the next article, we get stuck into trigonometry and its applications.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.