Year 9 Maths
Year 9 Maths tutoring at Matrix is known for helping students build a solid foundation.
Learning methods available
Select a year to see available courses

Are you confident with working out the surface areas of shapes? Don’t worry! This guide will provide you with the steps needed to find surface areas, examples and some sample questions and solutions for you to practice.
In this article we address the following syllabus outcomes:
Stage 5.3: Solve problems involving the surface areas of right pyramids, right cones, spheres and related composite solids (ACMMG271)
This unit exists because cylinders, cones, and spheres exist everywhere in the world from pyramids from ancient civilisations through to contemporary rockets like the Space-X Falcon 9. We need to able discuss the features of these shapes and to do this we need to be able to calculate things like their surface area.

You have already encountered some formulas for the surface area of different shapes.
Here are some examples:
| Solid | Formula for Surface Area |
| Cylinder | \(2 \pi r^{2}+2 \pi rh\) |
| Cone | \( \pi r^{2} + \pi rl \) |
| Sphere | \( 4\pi r^{2} \) |
You might be thinking, “Do I really have to memorise these formulas?”
No, not really! However, some are worth remembering because they will help you in the long run.
In this guide, we’ll break down each formula.
Understanding where each formula comes from is really important because it allows you to memorise less and tackle harder problems.
We’ll now take a look at each formula to see where it comes from. We’ll then see how this will help us to solve some harder problems.
We’re going to go through how you might find the surface area of a cylinder from scratch. Let’s take an imaginary cylinder of height \(h\) and radius \(r\) and open it up:
Doing this shows that a cylinder is made up of two circles and a rectangle. All we have to do now is to find the areas for each part and add them all up!
For both circles, they have a radius of \(r\). So, for each circle we have an area of \(\pi r^{2}\). This gives us the \(2 \pi r^{2}\) bit. That was easy!
The \( 2 \pi rh\) bit must then be given by the rectangle. One of the sides is the height of the cylinder \(h\).
The side which touches the circle will be “glued” to the edge of the circle when we make a cylinder. This means that its length is the same as the circumference of the circle \(2 \pi r\).
So, the area of the rectangle is given by \(h×2 \pi r = 2\pi rh\).
Adding the two contributions gives the total surface area: \(SA=2\pi r^{2}+2 \pi rh\). Check this with the formula given in the table above!
You see, we don’t need to remember the formula for the surface area of a cylinder. All we need to remember is how to calculate the area of the two circles and the area of the curved section (which is really a rectangle).
Join 4500 students who already have a head start and ace your Maths exams! Learn more about our Year 9 Maths Course.
To find the surface area of a cone, we need both its radius \(r\) and its slant height \(l\) (not the perpendicular height). We’ll also look at its net.
From the net, we see that we have a circle that comes from the base, as well as a sector of a circle.
The area of the circle is given by \(\pi r^{2}\) and the area of a sector is given by \(\pi rl\) (not required to know proof).
So, we immediately see that the surface area of the cone is given by \( SA = \pi r^2 + \pi rl \).
The only part that you really need to memorise is the area of the curved bit \(\pi rl\). Otherwise, this is fairly straightforward.
In some problems you might be told the perpendicular height, but not the slant height. In that case, you simply use Pythagoras’ theorem to find the slant height:
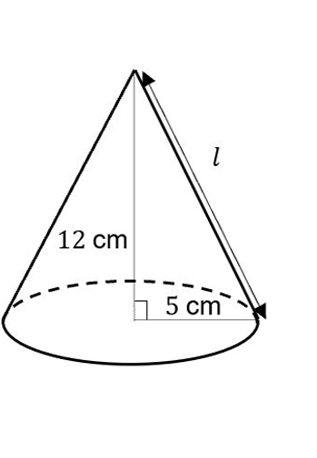
1. Find the slant height of a cone with radius 5 cm and perpendicular height 12 cm.
Drawing a picture and applying Pythagoras’ theorem gives:
The proof for the surface area of a sphere is beyond what you need to know.
So, this is one of the formulas that you just have to memorise.
However, it isn’t too bad to remember – just think of it as 4 times the area of the circle \(SA= 4\pi r^{2}\).
Typically, you’ll be asked to find the surface area of shapes like this:
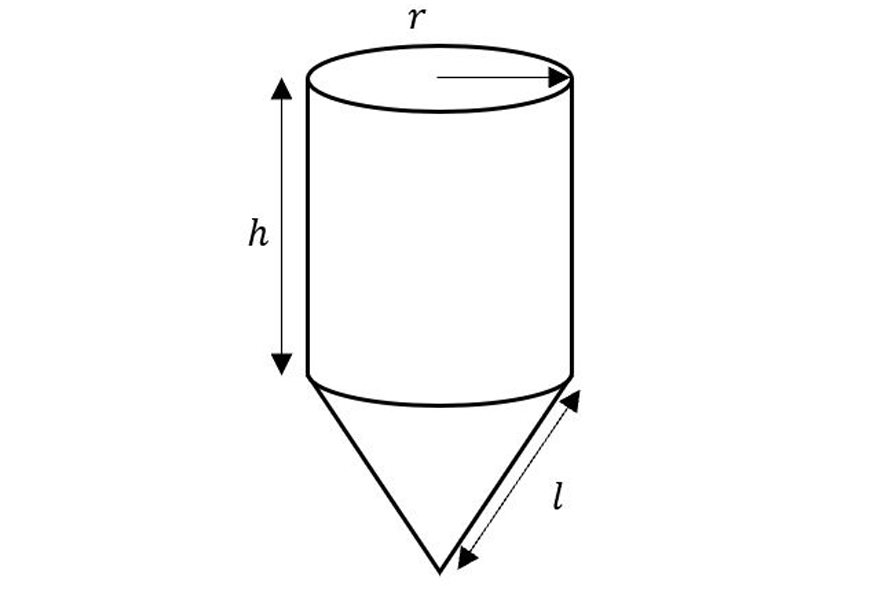
Here we’ve got a cylinder sitting on top of a cone.
We’ll need to use our formulas for the surface area of cones and cylinders but not directly.
For example, if we were naïve, we could take the surface area formulas of a cone and a cylinder and add them together to get \( SA=(\pi r^{2} + \pi rl) + (2 \pi r^{2} + 2 \pi rh)\).
Why wouldn’t this give us the right answer?
The problem is that we’ve counted the circle that is sandwiched between the cone and the cylinder twice, when we shouldn’t have even counted it in the first place!
Let’s have another go but being a bit more careful this time.
We’ll first break up the solid into simple parts where we can find the surface area of each part.
In our case, we’ve got a cone without its circular base as well as a cylinder without its top circle.
Now because we’ve thought about the surface area formulas, we know immediately that the cone bit gives \(\pi rl\) and the cylindrical bit gives \(\pi r^{2} + 2 \pi rh\) (one circle from the top).
So, the total surface area is \( SA = \pi rl + \pi r^{2} + 2 \pi rh\).
Let’s do another example, this time with numbers.
1. Find the surface area of the following solid:
Here, we have a hemisphere and a cone.
Note that the radius of the cone is the same as the radius of the hemisphere from the way they are attached i.e. 3 cm.
The surface area of the hemisphere, call it \(SA_{1}\) is given by:
\(SA_{1}=\frac{1}{2}×4 \pi r^{2} = 2 \pi (3)^{2}=18\pi\)
For the surface area of the cone, we need its slant height. This can be found using Pythagoras’ theorem since we know its perpendicular height and its radius:
\(So the surface area of the cone, call it \( SA_{2}\) is given by:
\(SA_{2}= \pi rl= \pi (3)(\sqrt{34})=3\sqrt{34}\pi\)
Note that we didn’t count the circular base because it isn’t part of the surface area. The total surface area is then:
\(SA=SA_{1}+SA_{2}\\
=18 \pi +3\sqrt{34} \pi \text{cm}^{2}\\
≈ 111.50 \text{cm}^{2}\)
If your final answer is a number, don’t forget to put the correct units down!
Let’s do one last example!
2. Find the surface area of the following pyramid whose perpendicular height is 4 cm:
For the base, we have a square whose area is \(SA_{1}=2×2=4\)
Since this is a square pyramid, all triangles are the same. To work out the area of the triangle, we will need the pyramid’s slant height
\(
Now each of the four triangles of the pyramid has base 2 cm and height \(\sqrt{17} \text{cm}\), so each triangle has area:
\(SA_2=\frac{1}{2}×2×\sqrt{17}=\sqrt{17}\)So, the total surface area is
\(SA=SA_1+4×SA_2=\\
To find the surface areas of composite solids:
Try to find the surface area of the following solids correct to 2 decimal places!
Check your own work with the worked solutions below.
1.
2.
3.
4. (Cylinder with inner section removed)
5.
6. (Cylinder with hemi-spherical cap)
7.
8.
9.
10. (Cube with cone placed on top)
1.
Area of base: \(SA_1=2×2=4\)
For each triangle: \(SA_2=1/2 (2)(5)=5\)
So \(SA=SA_1+4×SA_2=24 \text{cm}^2\)
2.
Area of base: \(SA_{\text{base}}=2×4=8\)
Slant heights: \(l_1=\sqrt{5^{2}+2^{2}}=\sqrt{29}\) ,
\(l_2=\sqrt{5^{2}+1^{2}}=\sqrt{26}\)
Area of triangles: \(SA_1=\frac{1}{2} (4) l_1\\
=2\sqrt{29}\) ,
\(SA_2=\frac{1}{2} (2) l_2=\sqrt{26}\)
\(SA=SA_{\text{base}}+2×SA_1+2×SA_2\\
=39.74 \text{cm}^2\)
3.
\(SA_{\text{prism}}=28 m^2\)
\(SA_{\text{pyramid}}=16 m^2\)
\(SA=SA_{\text{prism}}+SA_{\text{pyramid}}\\
=44 m^2\)
4.
Outer cylindrical sleeve: \(SA_1=2\pi rh=800\pi\)
Inner cylindrical sleeve: \(SA_2=400\pi\)
Area of each ring: \(SA_3=\pi (10)^{2}-\pi(5)^{2}\\
=75\pi\)
\(SA=SA_1+SA_2+2×SA_3\\
=1350\pi=4241.15 \text{cm}^{2}\)
5.
Cylindrical area: \(SA_1=\frac{1}{2} (2 \pi r^{2}+2 \pi rh)=\\
\frac{1}{2} (2\pi (0.5)^{2}+2 \pi (0.5)(10))=5.25 \pi \)
Area of rectangle: \(SA_2=1×10\\
=10\)
\(SA=SA_1+SA_2=26.49 m^2\)
6.
\(SA_{\text{hemisphere}}=\frac{1}{2}×4 \pi r^{2}=50 \pi\)
\(SA_{\text{cylinder}}= \pi r^{2} +2 \pi rh=75 \pi \) (\(r=5\))
\(SA=SA_{\text{hemisphere}}+SA_{\text{cylinder}}\\
=392.70 \text{cm}^{2}\)
7.
\(SA_{\text{cylinder}}=\pi r^2+2 \pi rh=39 \pi\)
\(SA_{\text{cone}}= \pi rl = 12 \pi \)
\(SA=SA_{\text{cone}}+SA_{\text{cylinder}}\\
=160.22 m^2\)
8.
\(SA_{\text{cylinder}}= \pi r^2+2 \pi rh=39 \pi\)
Slant height: \(l=\sqrt{3^2+4^2}=5\)
\(SA_{\text{cone}}=\pi rl=15\pi\)
\(SA=SA_{\text{cone}}+SA_{\text{cylinder}}\\
=169.65 m^2\)
9.
\(SA_{\text{top cone}}=3\pi \)
\(SA_{\text{bottom cone}}=12\pi\)
\( A_{\text{ring}}=\pi (2)^2-\pi (1)^2=3\pi\)
\(SA=SA_{\text{top cone}}+SA_{\text{bottom cone}}+A_{\text{ring}}\\
=54.55 m^2\)
10.
\(SA_{\text{cube}}=6×2^2=24\)
\(SA_{\text{cone}}= \pi rl=2 \pi \)
We also need to subtract off the area of the circle hiding underneath the cone:
\(A_{\text{circle}}=\pi(1)^2=\pi\)
\(SA=SA_{\text{cube}}+SA_{\text{cone}}-A_{\text{circle}}\\
=27.14 cm^2\)
Now that you know how to calculate surface area, you’re ready to learn how to calculate the volume of things.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.