Select a year to see courses
In this Guide, we will give you a comprehensive overview and cheat-sheet to help you conquer simultaneous equations for algebra!
Stage 5.3: Solves complex linear, quadratic, simple cubic and simultaneous equations and rearranges literal equations. (MAS.3-7NA)
Solve simultaneous equations, where one equation is non-linear, using algebraic and graphical techniques, including the use of digital technologies
These Syllabus Outcomes are telling you that you will learn how to solve simultaneous equations algebraically and graphically.
Algebra is used in every field of Maths:
In addition, algebra crops up in much of everyday life in fields like:
This article will show you the methods to solve simultaneous equations using two algebraic techniques (elimination and substitution) and graphically solve simultaneous equations.
We will also teach you to inspect the number of possible solutions to an equation without needing to solve it, by interpreting graphs.
Students should be familiar with:
So far in your study of algebraic equations, you will have only solved linear equations that contained one pronumeral.
Consider the following diagram:
The point \(P(x,y)\) satisfies two different equations because it lies on both of the lines.
The coordinate of this point gives the unique \(x\) and \(y\) values that satisfy both equations simultaneously.
Thus the two equations are called a pair of simultaneous equations.
We will first sketch each ‘equation’ as a line on the number plane and use these lines to find the solution to the pair of simultaneous equations.
The solution will reveal itself as the point of intersection of the two lines.
“The solution to a set of simultaneous equations is the common point of intersection”
Solve the equations \(x-y=2\) and \(3x+2y=6\) simultaneously, using the graphical method.
First sketch the lines \(y=x-2\) and \(y=-\frac{3}{2} x+3\) on the number plane.
We can see, graphically, that the two lines intersect at (2,0).
Thus (2,0) satisfies each equation.
Therefore, \(x=2\) and \(y=0\) are the solutions to the simultaneous equations.
The example given was very convenient – we were able to very clearly see where the two lines intersected.
But this will not always be the case, and in exam situations – we are not able to sketch the graphs with pin-point accuracy or be able to see what the solution is.
For example, solving the simultaneous equations
\(21x+5y+7=0\) and \(2x-3y-2=0\)
has solution \(x=-\frac{11}{73}\) and \(y=-\frac{56}{73}\). But it would have been extremely hard to see graphically!
We must, therefore, look at some more efficient ways to solve these equations.
Solving linear equations such as
\(x-2=\frac{(6-3x)}{2}\)are easy because there is only one unknown pronumeral.
So when faced with a pair of simultaneous equations, we can solve for one of the unknown variables and substitute it into the other equation.
This will reduce the problem to solving a linear equation just like the one we saw.
Once we solve for the variable, we can easily solve for the other variable since we can substitute it back into either one of the original equations.
Solve the equations \(x-y=2\) and \(3x+2y=6\) simultaneously using the substitution method.
Number the equations (so that we can talk about them easily):
\(Now we make y the subject in (1)
\(y=x-2\)and now substitute it into the other equation.
\(3x+2(x-2)=6\)which can be solved to obtain
\(x=2\).
We now solve for \(y\) by substituting \(x=2\) into either equation (it doesn’t matter!). At this point, it’s really up to you – but for this problem, it is easier to substitute it into (1):
\(2-y=2⇒y=0\)And so
\(x=2\) and \(y=0\)
is the solution.
Instead of substituting, which can often lead to a lot of algebra, sometimes we can more elegantly eliminate a variable from the equations to reduce it to a linear equation.
Often elimination method may require multiplying each of the equations by a constant before either adding or subtracting the two equations to eliminate the variable.
Solve the equations \(x-y=2\) and \(3x+2y=6\) simulteanously using the elimination method.
Number the equations:
\(Let’s now eliminate y, we can do this by first multiplying (1) by 2 and then adding up both of the equations.
\((1)+(2) gives
\(Notice how there were no y terms once we added up the equations. This is why it is called the ‘elimination’ method.
Once we have \(x=2\), we simply substitute it, just like before, into either equation to get \(y\)
And so
\(x=2\) and \(y=0\)
is the solution.
With the elimination method, often students will have to be a bit more creative in order to see what constants you may have to use when adding up or subtracting the equations.
This particular method might seem hard at first – but it will really start to pay off in more complicated simultaneous equation problems.
1. By graphing \(y=x+4\) and \(y=-x+2\) on the same number plane. Solve the equations \(x-y-4=0\) and \(x+y-2=0\) simultaneously.
2. Solve the equations \(x+2y-1=0\) and \(2x+5y-2=0\) simultaneously by using the substitution method.
3. Solve the equations \(2x-y+7=0\) and \(2x+5y-1=0\) simultaneously by using the elimination method.
1.
Drawing the two lines show that \(x=-1, y=3\) solves the pair of equations simultaneously.
2.
\(
x+2y-1=0…(1) \\
2x+5y-2=0…(2) \\
\)
From (1)
\(x=1-2y\)
Substitute this into equation (2)
\(
2(1-2y)+5y-2=0 \\
y=0 \\
\)
When \(y=0, x=1\)
Thus \(x=1\) and \( y=0\) solves the equations simultaneously
3.
\(
2x-y+7=0…(1) \\
2x+5y-1=0…(2) \\
(2)-(1): 6y-8=0 \\
∴y=\frac{4}{3} \\
\)
When \(y=\frac{4}{3},x=\frac{1}{2} (\frac{4}{3}-7)=-\frac{17}{6}\)
Thus \(x=-\frac{17}{6}\) and \(y=\frac{4}{3}\) solves the equations simultaneously.
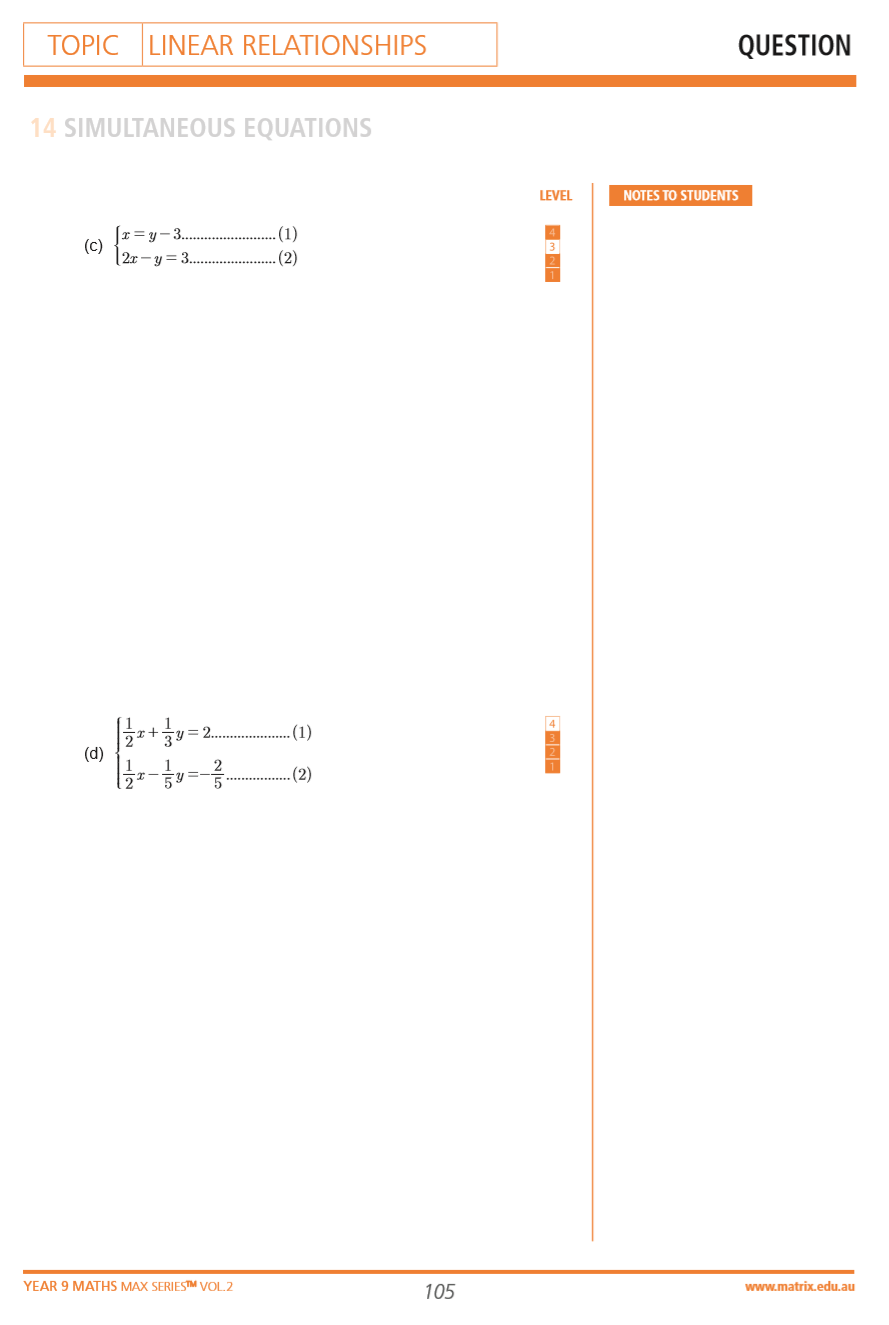
Be more prepared for your next ‘Simultaneous Equations’ exam with Year 9 Max Series Exam Preparation Book.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
