Welcome to Matrix Education
To ensure we are showing you the most relevant content, please select your location below.
Select a year to see courses
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Get HSC Trial exam ready in just a week
Get HSC exam ready in just a week
Select a year to see available courses
Science guides to help you get ahead
Science guides to help you get ahead


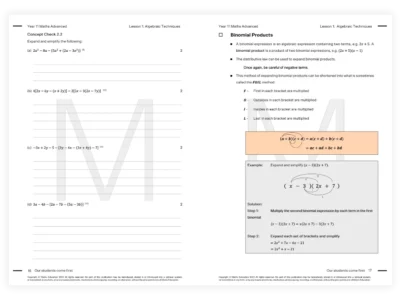
Our Year 11 Maths Advanced resources are designed by subject matter experts and cover all aspects of the new NSW Maths syllabus. Get ahead with 250+ pages of content, 100+ pages exam-style Workbook, quizzes, and a topic test for each module.


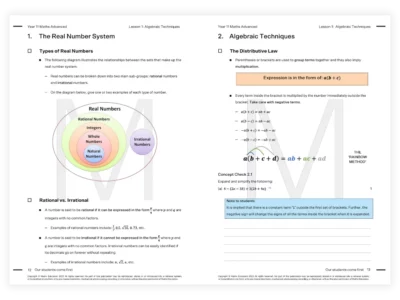
Matrix teachers are experts in their field with real teaching experience. Develop in-depth knowledge and understanding with our experienced teachers by applying our proven methods for Maths.

Step 1
Theory
Step 2
Application
Step 3
Guided Examples
Step 4
In-Class Practice
Step 5
Homework
Step 6
Videos for Revision
Step 7
Quizzes & Feedback
Discover and address gaps in your learning timely through weekly homework completion and quizzes.
See how our flexible learning methods can cater for your learning needs.

Experience engaging and interactive Maths Advanced lessons led by experienced Maths Advanced teachers.

Complete exam-style questions in your Work Book to consolidate your understanding of key concepts.
Revise areas of improvement from home anytime anywhere with online video lessons perfectly aligned with the Matrix Theory Book.

Build confidence for school assessments with weekly quizzes and the end of term Topic Test performed under strict exam conditions.
Matrix Term 1
(Oct - Dec)
Algebraic Techniques, Linear Functions, Absolute Values
Matrix Term 1
(Oct - Dec)
Algebraic Techniques, Linear Functions, Absolute Values
Matrix Term 2
(Feb - Apr)
Functions and Relations, Quadratics, Polynomials, Non-Linear Functions, Trigonometry
Matrix Term 2
(Feb - Apr)
Functions and Relations, Quadratics, Polynomials, Non-Linear Functions, Trigonometry
Matrix Term 3
(Apr - Jun)
Further Trigonometry, Introductory Calculus, Exponential and Logarithmic Functions
Matrix Term 3
(Apr - Jun)
Further Trigonometry, Introductory Calculus, Exponential and Logarithmic Functions
Matrix Term 4
(Jul - Sept)
Applications of Differentiation, Probability, Discrete Random Variables, Yearly Exam Revision
Matrix Term 4
(Jul - Sept)
Applications of Differentiation, Probability, Discrete Random Variables, Yearly Exam Revision
Matrix Term 1
(Oct - Dec)
Lesson 1: Algebraic Techniques
Lesson 2: Indices
Lesson 3: Surds
Lesson 4: Linear Equations & Inequalities
Lesson 5: Quadratic Equations
Lesson 6: Linear Functions
Lesson 7: Functions & Relations
Lesson 8: Absolute Values
Lesson 9: Topic Test
Matrix Term 2
(Feb - Apr)
Lesson 1: Working with Functions 1
Lesson 2: Working with Functions 2
Lesson 3: Working with Functions 3
Lesson 4: Further Functions and Relations
Lesson 5: Trigonometry 1
Lesson 6: Trigonometry 2
Lesson 7: Trigonometry 3
Lesson 8: Trigonometry 4
Lesson 9: Topic Test
Matrix Term 3
(Apr - Jun)
Lesson 1: Further Trigonometry 1
Lesson 2: Further Trigonometry 2
Lesson 3: Introductory Calculus 1
Lesson 4: Introductory Calculus 2
Lesson 5: Calculating with Derivatives
Lesson 6: Exponential Functions
Lesson 7: Logarithms 1
Lesson 8: Logarithms 2
Lesson 9: Topic Test
Matrix Term 4
(Jul - Sept)
Lesson 1: Review of Calculus
Lesson 2: Motion in a Straight Line
Lesson 3: Probability 1
Lesson 4: Probability 2
Lesson 5: Guided Practice Exam
Lesson 6: Discrete Random Variables 1
Lesson 7: Discrete Random Variables 2
Lesson 8: Discrete Random Variables 3
Lesson 9: Topic Test
Matrix teachers have the vast classroom teaching experience to clearly explain complex concepts.
Get 200+ page new-edition Theory Book written by expert teachers designed to help students develop in-depth knowledge and understanding in Mathematics.
Our small classes are arranged in a U-shape, creating an interactive and engaging learning environment.
Enjoy additional one-on-one tutor support for extra feedback, writing development, or homework assistance.
All Matrix Campuses are designed for student comfort and engagement. Make learning enjoyable with our comfortable and professional learning environment.
Online video lessons are conducted by experienced teachers who take you through the Matrix Theory Book step-by-step.
Track your child’s progress and achievement through Weekly Homework completion and Quizzes.
Get exam-ready with Topic Tests that consists of a variety of real exam-style questions.
Get year round access to Theory Lesson Videos, online resources, and track your progress easily via the Matrix LMS platform.
Want advice on your child’s learning? Get exclusive access to academic advice, and invitations to events and seminars from the Matrix academic team.
Enjoy access to all course resources until the end of the academic year.
All on campus courses come with our First Lesson Money Back Guarantee.
Learn at your own pace with the support you need. Work through your Matrix Theory Book with 8 clear video lessons taught by experienced Matrix teachers.

Address gaps in learning by asking questions on the student Q&A board to receive individual teacher support within 1 working day.
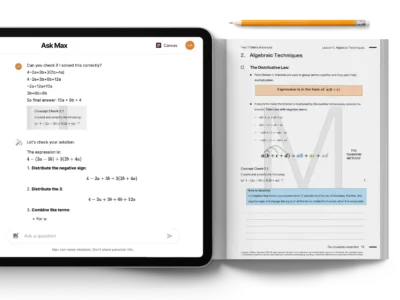
Receive instant explanations, personalised feedback, and step-by-step solutions anytime with your AI study companion, Ask Max.

Complete exam-style questions in your Work Book, online quizzes, and end-of-term Topic Tests to consolidate key concepts and build exam confidence.
Our carefully structured courses thoroughly cover all aspects of the NSW Year 11 Maths Advanced Syllabus. Each module is designed to address specific topics from the syllabus in a focused manner.
Module 1
Algebraic Techniques, Linear Functions, Absolute Values
Module 1
Algebraic Techniques, Linear Functions, Absolute Values
Module 2
Functions and Relations, Quadratics, Polynomials, Non-Linear Functions, Trigonometry
Module 2
Functions and Relations, Quadratics, Polynomials, Non-Linear Functions, Trigonometry
Module 3
Further Trigonometry, Introductory Calculus, Exponential and Logarithmic Functions
Module 3
Further Trigonometry, Introductory Calculus, Exponential and Logarithmic Functions
Module 4
Applications of Differentiation, Probability, Discrete Random Variables, Yearly Exam Revision
Module 4
Applications of Differentiation, Probability, Discrete Random Variables, Yearly Exam Revision
Module 1
Lesson 1: Algebraic Techniques
Lesson 2: Indices
Lesson 3: Surds
Lesson 4: Linear Equations & Inequalities
Lesson 5: Quadratic Equations
Lesson 6: Linear Functions
Lesson 7: Functions & Relations
Lesson 8: Absolute Values
Lesson 9: Topic Test
Module 2
Lesson 1: Working with Functions 1
Lesson 2: Working with Functions 2
Lesson 3: Working with Functions 3
Lesson 4: Further Functions and Relations
Lesson 5: Trigonometry 1
Lesson 6: Trigonometry 2
Lesson 7: Trigonometry 3
Lesson 8: Trigonometry 4
Lesson 9: Topic Test
Module 3
Lesson 1: Further Trigonometry 1
Lesson 2: Further Trigonometry 2
Lesson 3: Introductory Calculus 1
Lesson 4: Introductory Calculus 2
Lesson 5: Calculating with Derivatives
Lesson 6: Exponential Functions
Lesson 7: Logarithms 1
Lesson 8: Logarithms 2
Lesson 9: Topic Test
Module 4
Lesson 1: Review of Calculus
Lesson 2: Motion in a Straight Line
Lesson 3: Probability 1
Lesson 4: Probability 2
Lesson 5: Guided Practice Exam
Lesson 6: Discrete Random Variables 1
Lesson 7: Discrete Random Variables 2
Lesson 8: Discrete Random Variables 3
Lesson 9: Topic Test
200+ page new-edition Theory Book written by expert teachers designed to help students develop in-depth knowledge and understanding in Year 11 Maths Advanced course.
Learn from the best, with each Theory Lesson accompanied by Online Video Lessons led by experienced teachers.
Your personal AI study buddy, Max is here to assist anytime if you need feedback, explanations, or help with tricky questions.
Enjoy the flexibility of online learning with all the benefits of being on-campus. Lesson content progression is automatically unlocked for the best learning experience, ensuring students stay on track for success.
Discover your strengths and weaknesses with online Quizzes. And with automated marking, students receive instant feedback on their learning gaps.
Get exam-ready with Topic Tests that consists of a variety of real exam-style questions.
Stuck on a question? Address your individual learning needs by posting your questions on the Matrix Q&A Boards and receive responses within 1 working day.
Enjoy access to all course resources until the end of the academic year.
Want advice on your child’s learning? Get exclusive access to academic advice, and invitations to events and seminars from the Matrix academic team.
Online
| Access starts | 14 October 2024 |
| Access Ends | 31 December 2025 |
Matrix+ online
Term course
Holiday course
Who is it for?
Course structure
Matrix resources
Reporting
Additional support
Homework
Assessments









years teaching
Qualifications
Year levels
Subjects taught
Years at Matrix
years
Teaching experience
years
Campuses
Locations
Teaching methods
Flexible payment options: Pay quarterly or monthly over 3 months.
Term course
9 weekly lessons over 9 weeks
$1350
per module
$450
per month for 3 months
Matrix+ online
9 lessons anytime
$795
per module
$265
per month for 3 months
Matrix was honestly one of the best tutoring places I have ever been to. It was only through the experienced tutors and their brilliant guidance I was able to achieve Band 6’s in all my subjects and achieve a 99+ ATAR. I thank you Matrix and I cannot be anymore grateful.
The Year 11 Maths Extension provided me with a strong foundation on which to build a higher level of maths, coupled with extensive, thorough resources that never left me lacking questions! Moreover, my teacher was always engaging which made the lessons something to look forward to rather than dread.

Tara Anglican School for Girls
The Matrix Maths course has helped me lots with my school performance. The structure of Matrix, both in-person and through Matrix+ always gives me a boost, making me one term ahead of my peers.

Sydney Girls High School
I found the Year 12 Mathematics Advanced Matrix course really helpful. It assisted me with my integration skills and getting into good habits when dealing with and solving functions.

Pymble Ladies' College
Who are Matrix teachers?
Year 11 Maths Advanced Matrix tutoring teachers are experienced educators who have degrees in related disciplines. They are knowledgeable, know how to explain things clearly, and make learning fun.
What are the teaching styles of Matrix Maths teachers?
Matrix Year 11 Maths Advanced teachers deliver a structured and engaging learning experience through a mix of instructional and interactive teaching.
Is the Matrix Year 11 Maths Advanced tutoring program mapped to the New South Wales syllabus?
Yes, the Matrix Year 11 Maths Advanced course covers every aspect of the NSW Education Standards Authority (NESA) Syllabus thoroughly. It extends students’ abilities and helps them develop strong foundations in all aspects of Mathematics.
Why does Matrix teach one term ahead of the school program?
Matrix Term 1 starts in October each year. This allows students to learn one term ahead and gain a competitive advantage over their school peers when the topic is revisited at their school.
Can Matrix Year 11 Maths Advanced tutoring improve my child's marks at school?
100% of our students have reported an improvement in their confidence and marks since enrolling into the Matrix Year 11 Maths Advanced course.
How long does each Year 11 Maths tutoring session go for?
Each Year 11 Maths Advanced tutoring session is 90 minutes long and consists of Theory, Application and In-Class Practice. Refer to lesson structure for a detailed breakdown.
What is the class size?
All Matrix classes seat a maximum of 15 students arranged in U-shape formation to support an interactive and engaging student learning environment.
If my child misses a lesson, what can they do to catchup?
Matrix provides students access Online Theory Lesson Videos for missed lessons and revisions. The video lessons are easy to follow and paired with the Matrix Theory Book.
What is Matrix+?
Matrix+ is an online course consisting of video lessons paired with Matrix Theory Books. It’s accessible, more affordable and flexible compared to Matrix On-Campus courses. It’s an effective learning option if you prefer to learn at your own pace.
Is the online lesson live streamed classes?
No, you can learn at any time. Matrix+ lessons are pre-recorded to ensure the highest quality delivery for all types of learners! Our detailed video lessons allow you to view and follow the lesson at your own pace – pause, replay, or speed up videos for an on-demand learning experience.
How long do I have access Matrix+ course?
Year 11 Maths Advanced tutoring students will still be able to access Theory Lesson Videos, Q&A Discussion Boards, and online resources until the end of the calendar year.
How will I receive the Matrix+ Theory Book?
Matrix Theory Books will be mailed to your delivery address via Australia Post.