Select a year to see courses
Select a year to see available courses
Many concepts in Year 11 and 12 are built on Functions. So, it is extremely important that you become familiar with this concept to succeed in the HSC. In this Guide, we give you a comprehensive introduction to Year 10 functions, function notation, domain and range, and inverse functions.
Once we go through all the theory, there are checkpoint questions at the end to test your knowledge. We also have worked examples so you can see where you went right or wrong.
This article addresses the following syllabus outcomes:
All we are doing here is learning how to define function notation and use it to solve basic problems. You will develop this further when you study “Working with Functions” again in Years 11 and 12.
We’ll discuss the following topics:
Students should be:
With our Year 10 Maths Course, you will revise over core Maths topics, sharpen your skills and build confidence. Learn more now!
A relation is an expression that forms a relationship between two variables.
For example, the equations: \(y=x^2\) and \(x^2+y^2=1\) are known as relations because it relates \(x\) and \(y\) together.
Up to now, relations have only been described as linear and non-linear.
Like how quadrilaterals may be further defined as a rectangle or square, a relation can be called a function under special circumstances.
A function is a relation where for every x value there is only one y value.
Please note that while all squares are quadrilaterals, not all quadrilaterals are squares.
Similarly, all functions are relations but not all relations are functions.
Graphically, you can test if a relation is a function by using the vertical line test:
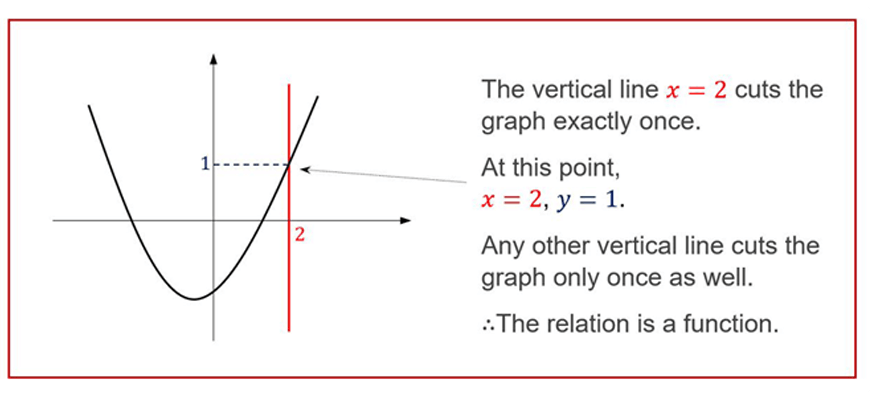
Determine which of the following graphs represents a function.
The above shows how we can graphically identify a function.
This section shows how to algebraically express functions using function notation.
The notation can be used to define a function.
For example, \(f(x)=3x-1\) represents the function \(y=3x-1\).
Often it is interpreted that:
\(y=f(x)\)
Similar notations like \(g(x), F(y),\) and \(L(t)\) can be used.
The first letter can be thought of as the ‘name’ of the function while the letter inside the brackets is the variable that the function represents.
For example, \(L(t)=t^2-3t+2\) is the function \(L\) in terms of \(t\).
When using this notation, \(f(a)\) indicates the value of \(y\) when \(x=a\).
∴To evaluate \(f(a)\), substitute \(a\) in for \(x\).
For the functions \(f(x)=x^2+x\) and \(g(x)=x+1\), find
1. \(f(2)\)
\(
2. \(f(1-a^2 )\)
\(
3. \(f(-x)\)
\(
4. \( f(g(x)) \)
\(
The last example, \( f(g(x)) \), is called a composite function because it is composed of two functions.
Being familiar with how to evaluate expressions such as \(\frac{(f(x+h)-f(x))}{h}\) is one of the most important skills required in Years 11 and 12, alongside with the concept of Domain and Range, and Inverse Functions (Ext 1).
These are covered below.
The domain of a relation is all of the permissible \(x\) values.
The range of a relation is all of the permissible \(y\) values.
Graphically, domain and range are the regions where there is a graph.
They can also be found algebraically using certain restrictions.
e.g. For \(\frac{1}{f(x)} , f(x)≠0\).
So any value of \(x\) where \(f(x)=0\) is excluded from the domain.
Find the domain and range for these relations.
1.
2. \(f(x)=\sqrt{(2x-1)}\)
1. From the graph:
\(x\) is only permitted to be between \(-3\) and \(3\). ∴Domain: \(-3≤x≤3\)
Similarly, \(y\) only takes values between \(-3\) and \(3\). ∴Range: \(-3≤y≤3\)
Note: There is no graph when \(x=4\) so it is not part of the domain.
2.
\(y=\sqrt{(2x-1)} \)
Domain:
Only positive values or zero can go underneath the square root.
∴\(2x-1≥0\)
∴\(x≥\frac{1}{/2}\)
∴ Domain:\( x≥\frac{1}{2}\)
Range:
\(\sqrt{(2x-1)}\) represents the positive square root.
∴\(\sqrt{(2x-1)}≥0\)
∴\(y≥0\)
Since \(y=\sqrt{(2x-1)}\)
∴Range: \(y≥0\)
There is one final component of this topic – Inverse Functions.
This part is seldom covered in Year 10 but will be introduced in Year 11, particularly Mathematics Extension 1.
The inverse of a function is simply the relation obtained by swapping \(x\) and \(y\) around.
Thus, for example, the inverse of \(y=2x-1\) can be found through these steps:
1. Interchange \(x\) and \(y\) Interchange \(x\) and \(y\)
\(x=2y-1\)
2. Make \(y\) the subject by rearranging
\(
When the inverse of a function also happens to be a function (like above), then it is called the inverse function of \(f(x)\), denoted by \(f^{-1} (x)\).
∴ In the above example, \(f^{-1} (x)=\frac{1}{2} x+\frac{1}{2}\).
Now given the graph of \(f(x)\), what would the graph of the inverse look like?
The answer is this:
The graphs of \(f(x)\) and its inverse are reflections of each other about the line \(y=x\).
1. Sketch the inverse of the following functions on the same number plane.
The second example shows that not every function has an inverse function.
This is because \(f^{-1} (x)\) fails the vertical line test. You can test if a function has an inverse function by using the horizontal line test.
Thus it is sometimes necessary to restrict the domain of so that it passes the horizontal line test, so that exists.
i.e. We will only examine a smaller portion of the domain where we know that an inverse function exists.
The graph of \(f(x)\) is shown below:
a. Explain why \(f(x)\) does not have an inverse function.
\(f(x)\) fails the horizontal line test.
b. Write down a possible domain for which \(f^{-1} (x)\) exists.
Many possible answers.
E.g. \(x≥0\) or \( x≤ \frac {-1}{2} \)
c. Write down the largest possible domain that includes the point (-1,-2), for which \(f^{-1} (x)\) exists. \(x≤\frac {-1}{2} \)
This is intended to be a very brief introduction to what inverse functions are about, however, can be a great source of revision once you have already learnt it in-depth.
1. Does the following graph represent a function?
2. Find \(f(2)\) if \(f(x)=x^3\).
3. State the domain and range of the relation in \(Q1 \).
4. Find the domain and range of \(y=x^2+1\).
5. Find the inverse of \(f(x)=x^3\).
6. On the same diagram, sketch the graphs of \(f(x)=x^3\) and its inverse. Does \(f(x)\) have an inverse function?
7. The graph of \(f(x)\) is shown below.
a) Explain why the domain of \(f(x)\) must be restricted if \(f(x)\) is to have an inverse function.
b) Write the largest possible domain that include the point \(P\), for which \(f^{-1} (x)\) exists.
8. Given \(f(x)=4x-x^2\), evaluate \(f(a^2+1)\).
9. Find the domain and range of \(y=\sqrt{(x^2+2x+10)}\).
10. Find the inverse relation of \(y=x^2+8x\) and state whether the inverse is a function.
1.
The relation is not a function as it fails the vertical line test.
2. \(f(2)=2^3=8\)
3. From the graph,
Domain: All real \(x\)
Range: \(y=-1, y=1\)
4. Domain: All real \(x\) [since there is no restriction on what x can be]
Range: Since \(x^2≥0\),
It follows that \(x^2+1≥1\) [add 1 to both sides]
∴\(y≥1\) [since \(y=x^2+1\)]
5. Rewrite \(f(x)=x^3\) as \(y=x^3\).
Interchange \(y\) and \(x\):
\(x=y^3\)
Make \(y\) the subject:
\(y=\sqrt[3]{x}\)
6.
\(f(x)\) passes the horizontal line test.
∴\(f^{-1} (x)\) exists. [Shown in red]
7.
a) On the given domain, \(f(x)\) fails the horizontal line test.
But for \(f^{-1} (x)\) to exist, \(f(x)\) must pass the horizontal line test, which can be achieved by restricting the domain of \(f(x)\) appropriately.
b)
\(\frac{-\pi}{2}≤x≤\frac{\pi}{2}\)
8.
\(f(a^2+1)=4(a^2+1)-(a^2+1)^2\) \(
9. Domain: Only non-negative values can go underneath the square root.
But note that \(x^2+2x+10\) is a concave up parabola that always lies above the x-axis.
∴\(x^2+2x+10>0\) for all \(x\)
∴ There is no restriction on what \(x\) can be
∴ Domain: All real \(x\)
Range: The vertex of \(x^2+2x+10\) is \((-1,9)\)
∴ The minimum value of \(x^2+2x+10\) is \(9\), i.e. \(x^2+2x+10≥9\)
∴\(\sqrt{(x^2+2x+10)}≥3\)
∴Range: \(y≥3\)
10.
\(The \(±\) indicates that the inverse is not a function.
Test: When \(x=0, y=-4±\sqrt{16}=-4±4=-8,0\)
∴The inverse is not a function, since there are two \(y\) values for a single value of \(x\).
Alternatively, since \(y=x^2+8x\) fails the horizontal line test, its inverse is not a function.
Being familiar with the concept of Functions is a major component to future success in mathematics.
You will meet Functions again in much greater depth in Years 11 and 12. We hope that this guide provides an easier transition from Year 10 to Year 11.
In our final article, we introduce you to logarithms. Logarithms are another subject that you will explore in much greater detail in Years 11 and 12.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
