Part 4: Year 10 Further Trigonometry (Applications)

Year 10 Further Trigonometry

In this article, Year 10 Further Trigonometry, we build on the concepts we learned in Part 3: Trigonometric ratios. Further Trigonometry involves applying what you’ve learned about ratios. You’ll learn how to use trigonometry to navigate or understand waves and frequencies.

We will walk you through how to apply your knowledge and then we’ll give you some concept check questions to check your progress.

Syllabus Outcomes

Here are the NESA Syllabus Outcomes that Year 10 further trigonometry students are meant to achieve.

• Applies trigonometry, given diagrams, to solve problems, including problems involving angles of elevation and depression.
• Applies trigonometry to solve problems, including problems involving bearings.
• Applies Pythagoras’ theorem, trigonometric relationships, the sine rule, the cosine rule and the area rule to solve problems, including problems involving three dimensions.

So, what do these mean for you? Remember when you did Trigonometry in Year 9? In this unit, you will build on that knowledge and what we looked at in Part 3. You will learn how to solve increasingly difficult and complex real-world problems.

Outline of Year 10 Further Trigonometry

Trigonometry has many applications in the real world. When translated to maths, this can introduce some interesting terminology and formulae. This subject guide will cover these formulae and terms and how they are used in maths questions related to trigonometry.

Assumed Knowledge

Before reading this guide, we assume you have got a firm grasp of:

• Algebraic techniques
• Graphing techniques
• Trigonometry fundamentals

To review your trigonometry fundamentals, check out our other subject guide: Trigonometric ratios.

Contents

In this guide, we will cover:

• Graphing trigonometric ratios
• The sine rule and cosine rule
• The area of a triangle formula
• Angles of elevation and depression, and trigonometry in three dimensions
• Directions and bearings

Summary

Trigonometric graphs take the form \(y=\sin x\). Like other graphs, we plot the function on our axes.

In sine graphs, it is recommended to draw the maximum and minimum bounds of the curve, as well as intercepts and critical points.

An example is shown below:

Sin graph

$$y=\sin(x)$$

Cos graph

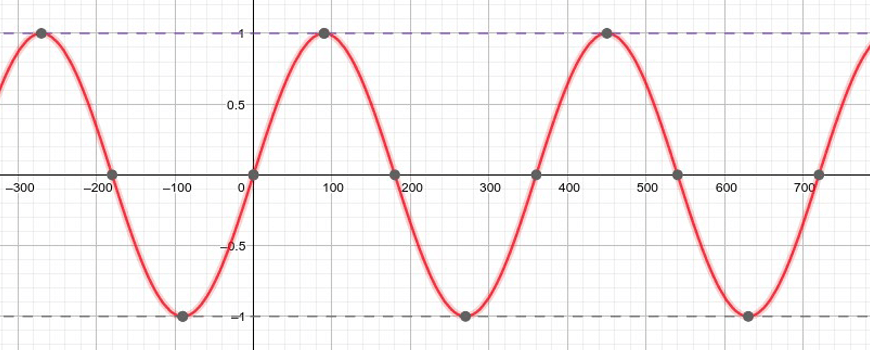
The x-intercepts are \(x=0, 180°, 360°\), and so on.

Cosine graphs are like sine graphs, except they start at 1 instead of 0:

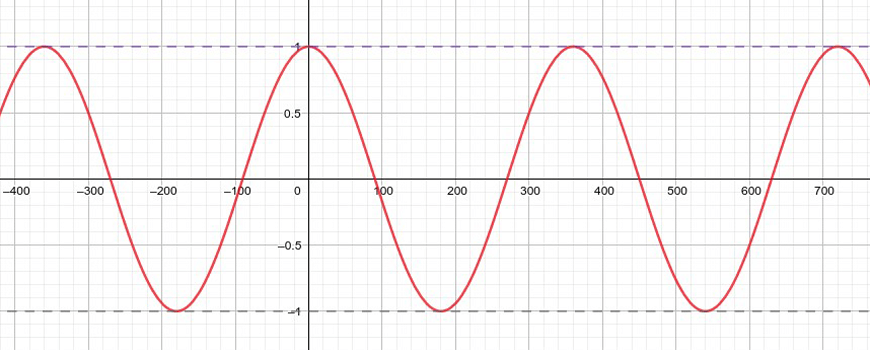
Consequently, the intercepts are also shifted: \(x=90°, 270°, 450°\), and so on.

Tan graph

The \(\tan\) graph is quite different: it repeats every  \(180°\), rather than every \(360°\).

When drawing \(\tan\) graphs take care to note the asymptotes.

Trigonometry ratio

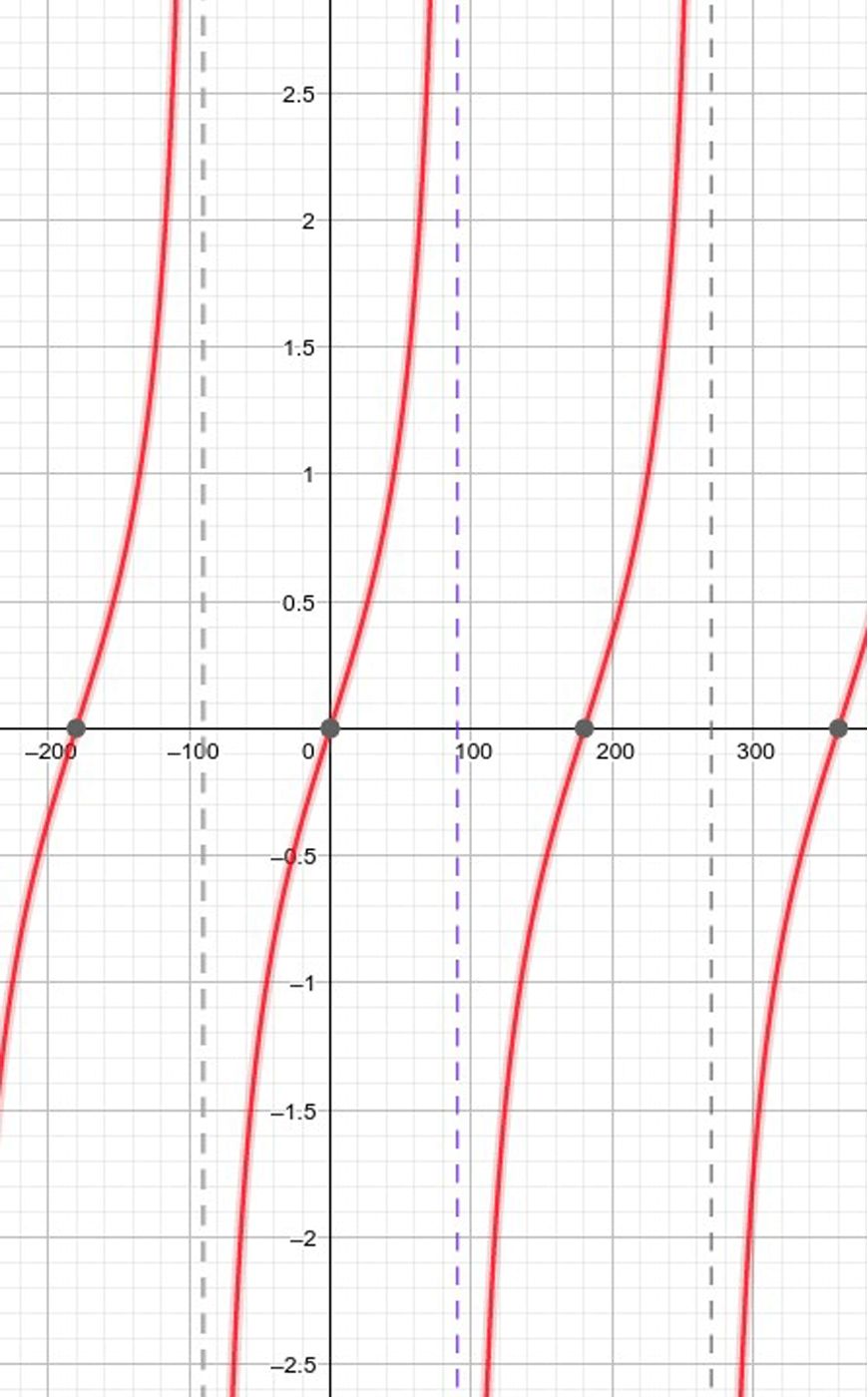
Three useful trigonometric results are the cosine rule, sine rule and the area of a triangle formula.

These work in any triangle, not just right triangles.

For the following examples, consider this triangle – note that side \(a\) is opposite angle \(A\), side \(b\) is opposite angle \(B\) and so on.

This is important.

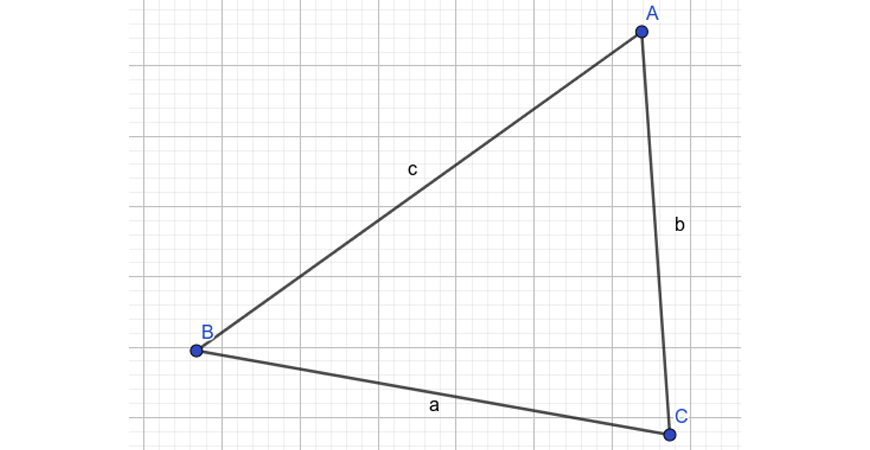
Cosine Rule

The cosine rule can be seen as an extension to the famous Pythagoras theorem:

$$c^2 = a^2 + b^2 – 2ab \cos C$$

Sine Rule

The sine rule is about ratios between angles and the sides opposite to each of them:

$$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$$

Area of a Triangle

The area of a triangle formula gives the area of a triangle:

$$\text{Area} = \frac{1}{2} ab \sin C$$

A variety of different terms are used to describe angles. These include:

• Angle of elevation: The angle between the line of sight and the horizontal, if the line of sight is above the horizontal.
• Angle of depression: The angle between the line of sight and the horizontal, if the line of sight is below the horizontal.

Because these angles are alternate angles across the parallel horizontals, they are equal.

When a third dimension is involved, the diagram will become more complex. Heights form 90° angles to distances, which often simplifies calculations.

You may also need to calculate directions. Terms used to describe angles in directions include:

• True bearing: This is the angle between North and the specified direction
  e.g. $$210°T$$
• Compass bearing: This is specified as North / South° East / West,
  for example  $$S 30° W$$

Checkpoint questions and solutions

Question

1. Graph the following equations.

a) $$3 \sin x + 1$$

b) $$\tan 2x$$

c) $$\sec x$$

2. Find all marked unknowns in the following triangles.

a)

b)

c)

3. Find the height of the tower in the diagram below to 2 decimal places.

4. Alice travels \(27km\) east from lighthouse P, which is \(30°T\) and \(43km\) from a rock Q. Calculate Alice’s relative position (bearing and distance) from Q.

Solutions

1.

a) To draw this graph, we shift the centre up 1 unit and make the amplitude 3 times larger.

b) Note how the coefficient inside the \(\tan\) function reduces the period to \(90°\), compared to the original period of \(180°\).

c. This means wherever the \(\cos\) graph had intercepts, the sec graph has asymptotes.

To graph this graph, plot a number of points and join them together, minding the intercepts.

Most students become familiar with this graph. Drawing the general shape and placing the intercepts and asymptotes correctly is enough to present as a solution.

2. Here we are given 2 sides and 1 angle, and we need to find an angle.

We can use the sine rule:

$$\frac{\sin32}{151} = \frac{\sin B}{155} $$

$$\sin B = \frac{155 \sin 32}{151}$$

$$=0.543$$

$$B = \sin^{-1} 0.543 = 33° \text{ (nearest degree)}]$$

However, the question is asking us to find \(x\); this can be done by considering the angle sum of a triangle:

$$x = 180-32-33 = 115°.$$

b.

For this question, we are asked to find a side.

We can use cosine rule here:

$$x^2=230^2 + 114^2 – 2 \times 230 \times 114 \times \cos 121$$

\(x=305.80 \text{ (2 d.p)}\) units.

c. To approach this question, we first divide the area into \(ABD\) and \(BCD\).

We can calculate the area of these two triangles using the area formula:

$$ABD = \frac{1}{2} \times 1.6 \times 2.5  \times \sin (98)=1.9 \text{units}^2$$

$$ BCD = \frac{1}{2} \times 2.3 \times 2.8  \times \sin (73)=3.1 \text{units}^2$$

$$\text{Total} = 5 \text{units}^2$$

3. Consider triangle \(PBC\): It is a right triangle, and so side \(BC\) can be expressed as

$$BC = \frac{h}{\tan 12}$$

Similarly in \(PBA\):

$$BA = \frac{h}{ \tan 7}$$

Now consider triangle \(ABC\). Using the cosine rule:

$$8^2 = BC^2+AB^2-2 \times AB \times BC \times \cos 11$$

Substituting for \(h\):

$$64 = \Big(\frac{h}{\tan12} \Big)^2 + \Big(\frac{h}{\tan 7} \Big)^2 – \frac{2 h^2 \cos 11}{ \tan 12 \tan 7}  $$

Hence $$h^2 = \frac{64}{ (\frac{1}{\tan12})^2 + (\frac{1}{\tan 7})^2 – \frac{2 \cos 11}{\tan 12 \tan 7}}$$

$$=4.834 $$

Hence $$h = 2.20 m \ (2 d.p.)$$

4. A good first step is to draw a diagram like the one above, drawing north / south lines where necessary to construct angles.

We can use the cosine rule in triangle \(PAQ\) to find \(AQ\);

$$AQ^2 = 27^2 + 43^2 – 2 \times 27 \times 43 \times  \cos 120$$

$$AQ = 61 km \text{(nearest km)}$$

Now we use the sine rule to find angle \(PQA\):

$$\frac{AQ}{\sin QPA} = \frac{AP}{\sin PQA}$$

$$\sin PQA = \frac{AP \sin QPA}{AQ}$$

$$PQA=13°$$

From north, this is $$13 + 30 = 43°$$

Hence \(A\) is \(61km\) from \(Q\) at a bearing of \(043°T\).

Additional Challenging Questions (From the MAX Series)

Questions

Answers

Confused about non-linear graphing?

In our next article, we show you how to solve and sketch non-linear equations as curves.