Select a year to see courses
Select a year to see available courses
These are the 2021 Maths Advanced HSC Solutions put together by the gurus from the Matrix Maths team. Read on to see how you went!
Join 75,893 students who already have a head start.
"*" indicates required fields
The 2021 HSC Mathematics Advanced (2 Unit) exam paper solutions are here!
Have you seen the 2021 HSC Mathematics Advanced (2 Unit) exam paper yet?
In this post, we will work our way through the 2021 HSC Maths Advanced (2 Unit) paper and give you the solutions, written by our Head of Mathematics Oak Ukrit and his team. (Doing practice papers? See the solutions for the 2020 HSC Maths Adv Exam here.)
Read on to see how to answer all of the 2021 questions.
| Question | Answer | Solution |
| 1. | B | \begin{align*} \sin^2 5x + \cos^2 5x &= 1 \\ \sin^2 5x &= 1 – \cos^2 5x \end{align*} |
| 2. | C | \begin{align*} E(X) &= \sum_{x = 1}^3 x P(X = x) \\ &= (1)(0.6) + (2)(0.3) + (3)(0.1) \\ &= 1.5 \end{align*} |
| 3. | D | Since a logarithm can only accept positive input, we must be constrained by \begin{align*} 1 – x &> 0 \\ – x &> -1 \\ x &< 1 \text{ or equivalently, } x \in (-\infty, 1) \end{align*} |
| 4. | C | Options (A) and (D) show that there are close to 100 downloads on day 1, which is not consistent with the graph given, so they are wrong. The graph given shows that the number of downloads increases from day 1 to day 10, and it decreases after that. Option (B) shows that the number of downloads every day is roughly the same, and that is inconsistent with the graph given. The graph in option (C) is consistent with all the features shown in the graph given. |
| 5. | A | Plugging in \(x = 0\) quickly gives the y-intercept as \(y = 10(0.8)^0 = 10\). Since the base of the exponential, \(0.8\), is less than one, then \(y\) should decrease as it takes on larger values of \(x\). |
| 6. | D | 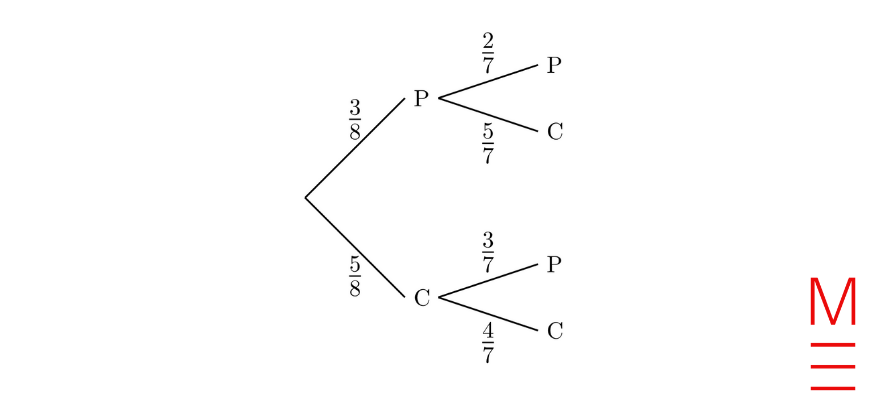 \begin{align*} |
| 7. | A | At \(x = -2\), the curve has a minimum turning point so \(f”(-2) > 0\). At \(x = 0\), the curve attains a negative y-intercept, so \(f(0) < 0\). At \(x = 3\), the curve has a maximum turning point, so \(f'(3) = 0\). Ordering from smallest to largest, we have \(f(0) < f'(3) < f”(-2).\) |
| 8. | C | The graph of \(y = f(x)\) has a single root at \(x = -1\) and a triple root at \(x = 3\), so the form of the polynomial is \(y = a(x + 1)(x – 2)^3\). The behaviour of the curve at the extremities implies the leading coefficient must be negative, which makes (C) the solution. |
| 9. | B | The derivative of \(h(x) = f(g(x))\) is \(h'(x) = f'(g(x)) g'(x)\) by the chain rule. We are given that the tangent to \(y = h(x)\) at \(x = k\) has the equation \(y = mx + c\), so the derivative at \(x = k\) must be the gradient. That is, \(h'(k) = m\). The gradient of the new tangent at \(x = -k\) is\begin{align*} h'(-k) &= f'(g(-k)) g'(-k) \\ &= f'(g(k)) g'(-k) & g(x) \text{ is even means } g(-x) = g(x) \\ &= f'(g(k)) [-g'(k)] & \text{Derivative of an even function is odd} \\ &= -h'(k) \\ &= -m \\ \end{align*}Since the tangent at \(x = k\) must intersect \(y = h(x)\), then \(h(k) = mk + c\).\begin{align*} h(-k) &= f(g(-k)) \\ &= f(g(k)) \\ &= mk + c \\ \end{align*}We can use point-gradient formula here,\begin{align*} y – (mk + c) &= -m(x + k) \\ y – mk – c &= -mx – mk \\ y &= -mx + c \\ \end{align*} |
| 10. | B | The overall picture is
Zooming into where the tangent touches the \(y = \cos x\) curve,
By considering the gradients of the above lines, we then have the ordering \(\frac{1}{2\pi} < m < \frac{1}{a}\) |
| \begin{align*} x + \frac{x – 1}{2} &= 9 \\ 2x + x – 1 &= 18 \\ 3x &= 19 \\ x &= \frac{19}{3} \end{align*} |
| \begin{align*} \cos 30^\circ &= \frac{XY}{16} \\ XY &= 16 \cos 30^\circ \\ &= 16 (\frac{\sqrt{3}}{2}) \\ &\approx 13.86 \; \text{cm} \text{(2 d.p.)} \end{align*} |
| \begin{align*} \text{Area of semicircle} &= \frac{1}{2} \times \pi(8)^2 \\ &= 32\pi \; \text{cm}^2 \end{align*} |
Using the Pythagorean theorem, we can complete the triangle as
| \begin{align*} \text{Area of triangle} &= \frac{1}{2}(8)(8 \sqrt{3}) \\ &= 32 \sqrt{3} \; \text{cm}^2 \end{align*}\begin{align*} \text{Total area of shaded region} &= \text{Area of semicircle} – \text{Area of triangle} \\ &= 32 \pi – 32 \sqrt{3} \\ &\approx 45.1 \; \text{cm}^2 \text{(1 d.p.)} \end{align*} |
| \begin{align*} y &= x \tan(x) \\ \frac{dy}{dx} &= 1 \times \tan(x) + x \times \sec^2(x) \\ &= \tan(x) + x \sec^2(x) \\ \end{align*}At \(x = \frac{\pi}{3}\),\begin{align*} \frac{dy}{dx} &= \tan(\frac{\pi}{3}) + \frac{\pi}{3} \sec^2(\frac{\pi}{3}) \\ &= \sqrt{3} + \frac{\pi}{3} \times \frac{1}{\frac{1}{4}} \\ &= \sqrt{3} + \frac{4\pi}{3} \end{align*}\(∴ \text{gradient of tangent at } x = \frac{\pi}{3} \text{ is } \sqrt{3} + \frac{4\pi}{3}\) |
| \begin{align*} S_n &= \frac{n}{2} \big(2 a + (n-1) d\big) \\ 2021 &= \frac{43}{2} \big(2 \times 5 + (43-1)d\big) \\ 94 &= 10 + 42d \\ d &= \frac{94 – 10}{42} \\ &= 2 \end{align*} |
| \begin{align*} \int_{-2}^0 \sqrt{2x + 4} \; dx &= \int_{-2}^0 (2x + 4)^{\frac{1}{2}} \; dx \\ &= \frac{2}{3} \times \frac{1}{2} \left[(2x + 4)^{\frac{3}{2}}\right]_{-2}^0 \\ &= \frac{1}{3} [4^{\frac{3}{2}} – 0] \\ &= \frac{8}{3} \end{align*} |
\(f(x) \text{ is increasing when } f'(x) > 0.\) \begin{align*} \(2x(1-3x) \geq 0\) |
(i)
| \begin{align*} y &= 29.2 – 0.011(540) \\ &= 23.26^\circ \text{C} \\ &\approx 23.3^\circ \text{C} \text{(1 d.p.)} \end{align*} |
(ii)
As the height of the town above sea level increases, the average maximum daily temperature decreases. Specifically, for every metre above sea level, there is approximately a \(0.011^\circ \text{C}\) decrease in the average maximum daily temperature. As the correlation coefficient is 0.494, there is a moderate negative correlation of this data.
Latitude would be a better predictor of the town’s average daily maximum temperature as there is a stronger negative correlation for this data of \(r = -0.897\) as opposed to only a moderate negative correlation coefficient of \(-0.494\) given by the comparison of the height above sea level and average daily maximum temperature.
Using sine rule in \(\triangle ABC\), let \(\angle ABC = \alpha\).
| \begin{align*} \frac{\sin(\alpha)}{25} &= \frac{\sin\left(28^\circ\right)}{16} \\ \sin(\alpha) &= \frac{25}{16} \sin(28^\circ) \\ ∴\alpha &= \sin^{-1}\left(\frac{25}{16} \sin(28^\circ)\right) \end{align*}The two solutions are,\begin{align*} ∴ \alpha &= \sin^{-1}\left(\frac{25}{16} \sin(28^\circ)\right) \text{, } 180^\circ – \sin^{-1}\left(\frac{25}{16} \sin(28^\circ)\right). \\ \end{align*}Since \(\alpha\) is obtuse,\begin{align*} ∴ \alpha &= 180^\circ – \sin^{-1}\left(\frac{25}{16} \sin(28^\circ)\right) \\ &\approx 133^\circ \; \text{(nearest degree)} \\ \end{align*} |
The graph of \(y = 2 + \frac{1}{x+4}\) is:
| \begin{align*} 2 \sin(4x) &= 1 \\ \sin(4x) &= \frac{1}{2} \end{align*}To solve for \(0 \leq x \leq \frac{\pi}{4}\), we need to solve the above trigonometric equation for \(0 \leq 4x \leq \pi\).\begin{align*} ∴ 4x &= \frac{\pi}{6}, \frac{5\pi}{6}. \\ ∴ x &= \frac{\pi}{24}, \frac{5\pi}{24}. \end{align*} |
The turning two turning points are at (0,0) and (2, -32) and \(x\)-intercepts at 0 and 3.
| \begin{align*} & 0.1915 – 0.0398 = 0.1517 \end{align*} |
| \begin{align*} & P(W > 3528) \\ &= P(Z > \frac{3528 – 3300}{570}) \\ &= P(Z > 0.4) \\ &= 1 – P(Z \leq 0) – P(0 < Z < 0.4) \\ &= 1 – \frac{1}{2} – 0.1554 \\ &= 0.3446. \end{align*}\begin{align*} ∴ \text{Expected number of babies out of } 1000 &= 1000 \times 0.3446 \\ &= 345 \text{(nearest whole baby)} \end{align*} |
First solve for \(b\) by substituting \(P = 1250\) and \(t = 20\),
| \begin{align*} 1250 &= 5000b^{-\frac{20}{10}} \\ \frac{1}{4} &= b^{-2} \\ b^2 &= 4 \\ ∴b &= 2 \text{ since } b \text{ is positive}. \end{align*}Differentiate \(P(t)\) in order to find \(t\) when \(\frac{dP}{dt} = -30\).\begin{align*} \frac{dP}{dt} &= \frac{5000 \times \ln{2} \times 2^{\frac{-t}{10}}}{-10} \\ &= -500 \times \ln{2} \times 2^{\frac{-t}{10}} \end{align*}Let \(\frac{dP}{dt} = -30\) and solve for \(t\),\begin{align*} -30 &= -500 \times \ln{2} \times 2^{\frac{-t}{10}} \\ 2^{\frac{-t}{10}} &= \frac{30}{500 \times \ln{2}} \\ \frac{-t}{10} &= \log_2 \left(\frac{30}{500 \times \ln{2}}\right) \\ ∴ t &= -10 \log_2 \left(\frac{30}{500 \times \ln{2}}\right) \\ ∴ t &\approx 35.3 \text{ years (1 d.p.)}. \\ \end{align*} |
| \begin{align*} \text{Shaded area} &= \frac{1}{2}(2)(3) + \int_{2}^4 \frac{3}{x – 1} \; dx \\ &= 3 + 3 \left[\ln{(x-1)}\right]_{2}^{4} \\ &= 3 + 3\left[\ln{(3)} – \ln{(1)}\right] \\ &= 3 + 3\ln{(3)} \\ &= 3 + \ln{(27)} \; \text{units}^2 \\ \end{align*} |
Using the table of future value interest factors for the first 8 years,
| \begin{align*} A &= 8.2132 \times 1000 \\ &= 8213.2 \end{align*}Leaving the money in her savings account for another 2 years at 1.25%,\begin{align*} A &= 8213.2 \times (1.0125)^2 \\ &\approx \$ 8419.81 \text{(2 d.p.)}. \end{align*} |
To find the maximum height, first differentiate \(y(t)\) with respect to \(t\).
| \begin{align*} y(t) &= -5t^2 + 70t + 100 \\ y'(t) &= -10t + 70 \\ y”(t) &= -10 \\ \end{align*} Stationary point is attained when \(y'(t) = 0\), so substituting in, \begin{align*} y'(t) &= 0 \\ -10t + 70 &= 0 \\ ∴ t &= 7 \end{align*} Verify that \(t = 7\) is a maximum because \(y”(7) = -10 < 0\).Hence, the maximum height reached by the particle is,\begin{align*} y(7) &= -5(7)^2 + 70(7) + 100 \\ y(7) &= 345 \text{ m} \\ \end{align*} |
In order to find the velocity, i.e. \(y'(t)\) of the particle before hitting the ground. First find \(t\) when the particle has a height of zero, i.e. \(y(t) = 0\).
| \begin{align*} y(t) &= 0 \\ -5t^2 + 70t + 100 &= 0 \text{(use quadratic formula)}\\ ∴ t &= 7 \pm \sqrt{69} \end{align*}Since \(7 – \sqrt{69} < 0\), then the particle hits the ground when \(t = 7 + \sqrt{69}\). Then, we will only find \(y'(7 + \sqrt{69})\),\begin{align*} y'(7 + \sqrt{69}) &= -10(7 + \sqrt{69}) + 70 \\ &= -70 – 10\sqrt{69} + 70 \\ &= – 10\sqrt{69} \end{align*}\(∴\text{ velocity } = -10 \sqrt{69} \; \text{m}^2\) |
The turning point below is at (6,400) where the x-intercepts are at 0 and 12.
| \begin{align*} E &= \int_{a}^{b} P(t) \; dt \\ &= \int_{a}^{b} 400 \sin\left( \frac{\pi}{12} t\right) \; dt \\ &= \frac{400 \times 12}{\pi} \left[ -\cos\left( \frac{\pi}{12}t\right)\right]_{a}^{b}\; dt \\ &= \frac{4800}{\pi} \left[ \cos\left( \frac{a\pi}{12}\right) – \cos\left( \frac{b\pi}{12}\right)\right] \\ \end{align*} |
Use part (b) and let \(a = 3\) and \(E=300\), then solve for \(b\).
| \begin{align*} 300 &= \frac{4800}{\pi} \left[ \cos\left( \frac{3\pi}{12}\right) – \cos\left( \frac{b\pi}{12}\right)\right] \\ \frac{300 \pi}{4800} &= \frac{1}{\sqrt{2}}- \cos\left( \frac{b\pi}{12}\right) \\ \cos\left( \frac{b\pi}{12}\right) &= \frac{1}{\sqrt{2}} – \frac{\pi}{16} \\ b &= \frac{12}{\pi} \cos^{-1} \left(\frac{1}{\sqrt{2}} – \frac{\pi}{16}\right) \\ b &\approx 3.95238 \end{align*}Hence, waiting time is\begin{align*} b – a &= 3.95238 – 3 \\ &= 0.95238 \; \text{hours} \\ &\approx 57.142 \; \text{minutes} \end{align*}Therefore, the least amount of time that Kenzo must wait to the nearest minute is 58 minutes. |
From the graph drawn in part (a), we can observe that the maximum power output is attained 6 hours after sunrise. Thus it would not require as long for Kenzo to charge his phone starting from 6 hours after sunrise as compared to starting from 3 hours after sunrise.
First find the x-intercept of the function \(f(x) = 8 – 2^x\).
| \begin{align*} 0 &= 8 – 2^x \\ 2^x &= 8 \\ ∴ x &= 3 \end{align*}Next, integrate \(f(x)\) from 0 to 3 in order to find the area under the curve.\begin{align*} \text{Area} &= \int_{0}^{3} 8 – 2^x \; dx \\ &= \left[ 8x – \frac{2^x}{\ln{(2)}}\right]_{0}^{3} \\ &= \left(8(3) – \frac{2^{(3)}}{\ln{(2)}}\right) – \left( 8(0) – \frac{2^{(0)}}{\ln{(2)}}\right) \\ &= 24 – \frac{8}{\ln(2)} + \frac{1}{\ln(2)} \\ &= 24 – \frac{7}{\ln{(2)}} \end{align*} |
The graph below has an x-intercept at 2 and asymptote of \(y=-8\).
| \begin{align*} \int_{2}^{5} g(x) \; dx &= \int_{-3}^{0} -f(-x) \; dx \\ &= \int_{0}^{3} -f(x) \; dx \\ &= – \int_{0}^{3} f(x) \; dx \\ &= – \left[ 24 – \frac{7}{\ln{(2)}}\right] \\ &= \frac{7}{\ln{(2)}} – 24 \end{align*} |
Let \(A_n\) be the amount in the account on Megan’s n-th birthday.
| \begin{align*} A_1 &= 5000(1.03) + 1000 \\ A_2 &= A_1(1.03) + 1000 = 5000(1.03)^2 + 1000(1.03) + 1000 \\ A_3 &= A_2(1.03) + 1000 = 5000(1.03)^3 + 1000(1.03)^2 + 1000(1.03) + 1000 = \$8554.54 \end{align*} |
We are given that \(A_{17} = 30 025.83\).
Let \(B_n\) be the amount in the account after the n-th annual withdrawal.
| \begin{align*} B_1 &= A_{17}(1.03) – 2000 \\ B_2 &= A_{17}(1.03)^2 – 2000(1.03) – 2000 \\ &\vdots \\ B_n &= A_{17}(1.03)^n – 2000[(1.03)^{n-1} + (1.03)^{n-2} + \dots + 1.03 + 1] \\ &= A_{17}(1.03)^n – \frac{2000(1 – 1.03^n)}{1 – 1.03} \end{align*}Solve for \(B_n = 0\),\begin{align*} A_{17}(1.03)^n – \frac{2000(1 – 1.03^n)}{1 – 1.03} &= 0 \\ A_{17}(1.03)^n – \frac{2000}{-0.03} + \frac{2000(1.03)^n}{-0.03} &= 0 \\ \left(A_{17} – \frac{2000}{0.03}\right)(1.03)^n &= – \frac{2000}{0.03} \\ (1.03)^n &= – \frac{2000}{0.03} \times \frac{1}{A_{17} – \frac{2000}{0.03}} \\ n &= \frac{1}{\ln(1.03)} \ln \left(-\frac{2000}{0.03} \times \frac{1}{A_{17} – \frac{2000}{0.03}}\right) \\ &\approx 20.249 \end{align*}Hence, Megan can make a maximum of 20 withdrawals of \(\$2,000\) before her account balance is insufficient. |
Solve for \(x\) when \(F(x) = 0.99\)
| \begin{align*} 0.99 &= 1- e^{-0.01x} \\ e^{-0.01x} &= 0.01 \\ -0.01x &= \frac{\ln{(0.01)}}{-0.01} \\ ∴ x &= 460.52 \text{ hours (2 d.p.)} \\ \end{align*} |
| \begin{align*} y &= x^2 – 1\\ \frac{dy}{dx} &= 2x \end{align*}Equate the gradient of the tangent when \(x = a\) with the gradient of the line that passes through \((3, -8)\) and \((a, a^2-1)\),\begin{align*} \frac{-8 – (a^2 – 1)}{3 – a} &= 2(a) \\ -8 – a^2 + 1 &= 6a – 2a^2 \\ a^2 – 6a -7 &= 0 \\ (a – 7)(a + 1) &= 0 \\ ∴ a &= 7, -1 \end{align*}Therefore, the two points on \(y = x^2-1\) where their tangents pass through \((3,-8)\) are \(A(7,48)\) and \(B(-1, 0)\). Using the point-gradient formula, the equation of the tangent at \(A(7,48)\) is\begin{align*} y – 48 &= 14(x – 7) \\ y &= 14x – 98 + 48 \\ ∴ y &= 14x – 50 \end{align*}Similarly for \(B(-1,0)\),\begin{align*} y – 0 &= -2(x + 1) \\ ∴ y &= -2x – 2 \end{align*} |
Let \(X\) be a female’s height in the population and \(Y\) be a male’s height.
| \begin{align*} P(X< 175) &= 97.5\% \\ P(X < 160.6) &= 16\% \\ P(Y < h) &= 84\% \end{align*}Our aim is the find \(h\). Using the empirical rule with the information given above.\begin{align*} \mu + 2\sigma &= 175 & \text{(1)} \\ \mu – \sigma &= 160.6 & \text{(2)} \end{align*}Subtracting equation (1) by (2) gives\begin{align*} 3 \sigma &= 14.4 \\ ∴ \sigma &= 4.8 \end{align*}Substitute \(\sigma = 4.8\) into (1),\begin{align*} \mu + 2(4.8) &= 175 \\ \mu = 165.4 \end{align*}Hence, for the adult male population, the mean is \(1.05 \mu = 173.67\) and the standard deviation is \(1.1 \sigma = 5.28\). Since being \(84\%\) taller than the male population is 1 standard deviation above the mean, then we can calculate \(h\) as\begin{align*} h &= 1.05 \mu + 1.1 \sigma \\ &= 173.67 + 5.28 \\ &= 178.95 \; \text{cm} \end{align*} |
Using the fact that the total probability is always \(1\),
| \begin{align*} \int_{-\infty}^{\infty} f(x) \; dx &= 1 \\ \int_{0}^{6} \frac{Ax}{x^2 + 4} \; dx &= 1 \\ A \left[\frac{1}{2} \ln{(x^2 + 4)}\right]_{0}^{6} &= 1 \\ \frac{A}{2}\left[\ln(40) – \ln(4)\right] &= 1 \end{align*}\begin{align*} ∴ A &= \frac{2}{\ln{(40)} – \ln{(4)}} \\ &= \frac{2}{\ln(\frac{40}{4})} \\ &= \frac{2}{\ln(10)} \end{align*} |
Find when the first derivative is equal to zero to find the maximum turning point.
The first derivative is
| \(\frac{dy}{dx} = \frac{2}{\ln{(10)}} \left[\frac{4 – x^2}{(x^2+4)^2} \right]\) Solve for \(\frac{dy}{dx} = 0\),\begin{align*} \frac{2}{\ln{(10)}} \left[\frac{4 – x^2}{(x^2+4)^2} \right] &= 0 \\ 4 – x^2 &= 0 \\ x &= \pm 2 \\ ∴x &= 2 \text{ since } x \in [0, 6] \\ \end{align*} |
| \begin{align*} P(X < 2) &= \int_{0}^{2} \frac{Ax}{x^2 + 4} \; dx \\ &= \frac{2}{\ln{(10)}}\left[\frac{1}{2} \ln{(x^2+4)} \right]_{0}^{2} \\ &= \frac{1}{\ln{(10)}} \left[\ln{\left(2^2 + 4\right)} – \ln{\left(0^2 + 4\right)} \right] \\ &= \frac{1}{\ln{(10)}} \left[\ln{(8)} – \ln{(4)} \right] \\ &= \frac{\ln{\left(\frac{8}{4} \right)}}{\ln{(10)}} \\ &= \frac{\ln{(2)}}{\ln{(10)}} \\ ∴ P(X <2) &= \log_{10}{(2)} \text{(using change of base rule)}\\ \end{align*} |
We can write the following facts by using the empirical rule and results from previous parts:
| \begin{align*} &P(IQ > 130) = 2.5\% = 0.025 \\ &P(X < 2) = \log_{10}{(2)} \\ &P(X < 2 | IQ > 130) = 80\% = 0.8 \end{align*}The aim is to find the probability that a person has an IQ greater than 130, given that they can complete the puzzle in less than two hours. That is, we want to find \(P(IQ > 130 | X < 2)\),\begin{align*} P(IQ > 130 | X < 2) &= \frac{P(IQ < 130 \text{ and } X < 2)}{P(X < 2)} \\ &= \frac{P(X < 2| IQ > 130) \times P(IQ > 130)}{P(X < 2)} \\ &= \frac{0.8 \times 0.025}{\log_{10}(2)} \\ &\approx 0.066 \text{(3 d.p.)} \end{align*} |
| \begin{align*} E\left(X\right) &= r \times r^n + r^2 \times r^{n – 1} + … + r^{k} \times r^{n – k + 1} + .. + r^n \times r \\ E\left(X\right) &= r^{n + 1} + r^{n + 1} + … + r^{n + 1} \text{ (the summation is $r^{n + 1}$ summed $n$ times)} \\ E\left(X\right) &= n(r^{n + 1}) … (1)\\ \end{align*}Also note that the summation of the probabilities equate to one.\begin{align*} \sum_{x}P(X = x) &= 1 \\ r^n + r^{n – 1} + … + r &= 1 \\ \frac{r \times (1 – r^n)}{1 – r} &= 1 \\ ∴ r^{n+1} &= 2r – 1 … (2)\\ \end{align*}By substituting equation (2) into equation (1),\begin{align*} ∴ E\left(X\right) &= n(2r – 1) \\ \end{align*} |
Written by Matrix Maths Team
The Matrix Maths Team are tutors and teachers with a passion for Mathematics and a dedication to seeing Matrix Students achieving their academic goals.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
