Select a year to see courses
In this post, we give you the solutions to the 2020 Maths Advanced paper.
Join 75,893 students who already have a head start.
"*" indicates required fields
The 2020 HSC Mathematics Advanced (2 Unit) exam paper solutions are here!
Have you seen the 2020 HSC Mathematics Advanced (2 Unit) exam paper yet?
In this post, we will work our way through the 2020 HSC Maths Advanced (2 Unit) paper and give you the solutions, written by our Head of Mathematics Oak Ukrit and his team.
In this video, Head of Maths Oak Ukrit solves the common questions from the 2020 HSC Maths Advanced and Maths Standard 2 papers.
Read on to see how to answer all of the 2020 questions.
| Question Number | Answer | Solution |
| 1. | D | We can only take the square root of non-negative numbers, so we need \( 2x – 3 \geq 0 \). This means that \( 2x \geq 3, so \ x \geq \frac{3}{2}\). |
| 2. | B | The graph is translated right as we have \( (x \ – \ 2)\) and the graph is translated up as we have \( +5 \). |
| 3. | A | \begin{align*} z_{French} \ &= \ \frac{82-70}{8} \ = \ 1.5 \\ z_{Commerce} \ &= \ \frac{80-65}{5} \ = \ 3 \\ z_{Music} \ &= \ \frac{74-50}{12} \ = \ 2 \end{align*}Comparing z-scores, his weakest subject is French and his strongest subject is Commerce. |
| 4. | B | \( \int e + e^{3x} \, dx = ex + \frac{1}{3} e^{3x} + c \), where \( c \) is a constant. |
| 5. | C | Here, \( a < 0 \) so the parabola \( y = -x^2 + bx + 1 \) should be concave down. Furthermore, the axis of symmetry is \begin{align*} since it is given that \( b > 0 \) . |
| 6. | B | Since \( -1 \leq \cos 3x \leq 1\) , and multiplying everything by \( 2 \) gives \( -2 \leq 2 \cos 3x \leq 2\). Adding \( 5 \) to everything gives \( 5 – 2 \leq 5 + 2 \cos 3x \leq 5 + 2 \) , so \( 3 \leq 5 + 2 \cos 3x \leq 7\) . Therefore, the range of \( 5 + 2 \cos 3x\) is \( [3,7]\). |
| 7. | A | \begin{align*} \int_0^{12} f\left(x\right) \, dx &= \text{area under $f\left(x\right)$ from $0$ to $12$} \\ &= 3 \times 4 + 3 \times 4 + \frac{1}{2} \times \pi \times \left(\frac{8 – 4}{2}\right)^2 + \frac{3 \times \left(10 – 8\right)}{2} – \frac{3 \times \left(12 – 10\right)}{2} \\ &= 12 + 12 + 2 \pi + 3 – 3 \\ &= 24 + 2 \pi \,. \end{align*} |
| 8. | A | 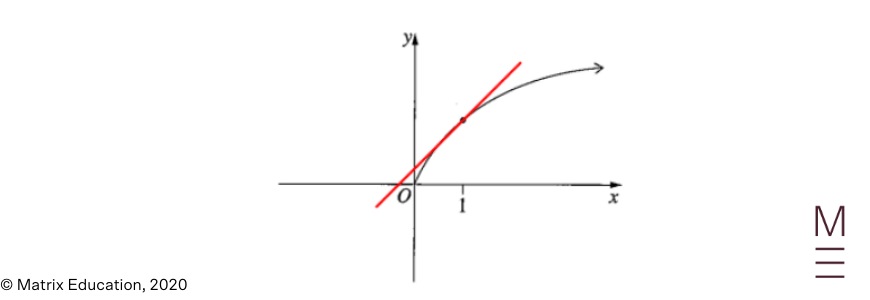 The answer is A. We have \begin{align*} since it is above the \( x \) -axis. The graph is concave downwards so \begin{align*} By considering the tangent to \( y = f(x) \) that passes through the points \( (0, c)\) and \( (1, f(1))\), we have \begin{align*} Also, the slope of the tangent to \( f(x) \) at \( x = 1 \) is positive, so \begin{align*} In conclusion, \begin{align*} |
| 9. | C | We can make the following markings on the normal curves provided:
Only C then has the lower bound of \( 10\% \) and the upper bound of \( 25\% \) in the correct regions. |
| 10. | D | There are 2 maximum stationary points at \(? = 1\) and since \(?(?)\) is continuous, there must be a minimum stationary point in between. Therefore \(3\) stationary points in total. |
The volume of water in Tank B is \( V = 30t + b \) . Substituting \( V = 0 \) and \( t = 15 \) into the equation gives
| \begin{align*} 0 &= 30\left(15\right) + b \\ 0 &= 450 + b \\ b &= -450 \ \end{align*} |
This means that the volume of water in Tank B is
| \( V = 30t – 450\) |
It is given that the volume of water in Tank A is
| \( V = 1000 – 20t \) |
So the two tanks have the same volume of water when
| \begin{align*} 30t – 450 &= 1000 – 20t \\ 1450 &= 50t \\ t &= \frac{1450}{50} \\ t &= 29 \end{align*} |
Therefore, at \( t = 29 \) minutes, they contain the same volume of water.
When the total volume of water in the two tanks is \( 1000 \) litres, we have
| \begin{align*} (1000 – 20t) + (30t – 450) &= 1000 \\ 550 + 10t &= 1000 \\ t &= \frac{1000 – 550}{10} \\ t &= 45 \end{align*} |
Therefore, at \( t = 45 \) minutes, the total volume of water in the two tanks is \( 1000 \) litres.
The common difference is
| \begin{align*} d &= T_2 – T_1 \\ &= 10 – 4 \\ &= 6 \end{align*} |
The first term is
| \( a = 4 \) |
Using
| \( T_n = a + (n – 1) d \) |
we have
| \begin{equation*} 1354 = 4 + (n – 1) (6) \,, \end{equation*} |
so
| \begin{align*} n &= \frac{1354 – 4}{6} + 1 \\ &= 226 \end{align*} |
Therefore, the sum of the arithmetic series is
| \begin{align*} S_{226} &= \frac{226}{2} (4 + 1354) \\ &= 153454 \end{align*} |
We have
| \begin{align*} \int_0^{\pi/4} \sec^2 x \, dx &= \left[\tan x\right]_0^{\pi/4} \\ &= \tan \left(\frac{\pi}{4}\right) – \tan \left(0\right) \\ &= 1 – 0 \\ &= 1 \ \end{align*} |
We have
| \begin{align*} n \left(H \cup G\right) &= n \left(H\right) + n \left(G\right) – n\left(H \cap G\right) \\ 33 &= 20 + 18 – n \left(H \cap G\right) \\ n\left(H \cap G\right) &= 5 \,. \end{align*} |
Therefore,
| \begin{align*} P\left(H \cap G\right) &= \frac{5}{40} \\ &= \frac{1}{8} \,. \end{align*} |
We have
| \begin{align*} P \left(\overline{H} \,|\, G\right) &= \frac{P\left(\overline{H} \cap G\right)}{P\left(G\right)} \\ &= \frac{13}{18} \,. \end{align*} |
The probability required is
| \begin{align*} P\left(H\right) \times P\left(\overline{H}\right) &= \frac{20}{40} \times \frac{20}{39} \\ &= \frac{10}{39} \,. \end{align*} |
We have
| \begin{align*} \angle APB &= \angle NPB – \angle NPA \\ &= 100º – 35º \\ &= 65º \end{align*} |
as required.
Using the cosine rule, we have
| \begin{align*} AB^2 &= AP^2 + PB^2 – 2 \times AP \times PB \times \cos 65º \\ &= 7^2 + 9^2 – 2 \times 7 \times 9 \times \cos 65º \\ &= 76.75 \end{align*} |
so
| \begin{align*} AB &= \sqrt{76.75} \\ &= 8.76 \ \text{km} \quad \text{(correct to 2 d.p.)} \end{align*} |
Using the cosine rule, we have
| \begin{equation*} PB^2 = AP^2 + AB^2 – 2 \times AP \times AB \times \cos (\angle PAB) \end{equation*} |
Rearranging this gives
| \begin{align*} \cos (\angle PAB) &= \frac{AP^2 + AB^2 – PB^2}{2 \times AP \times AB} \\ &= \frac{7^2 + 76.75 – 9^2}{2 \times 7 \times 8.76} \\ &= 0.365 \end{align*} |
so
| \begin{align*} \angle PAB &= \cos^{-1} \left(0.365\right) \\ &= 68º 36′ \\ &\approx 69º \end{align*} |
Therefore,
| \begin{align*} \text{bearing} &= 180º – (69º – 35º) \\ &= 146º \quad \text{(correct to the nearest degree)} \,. \end{align*} |
Calculating the derivatives gives
| \begin{align*} \frac{dy}{dx} &= \frac{d}{dx} (-x^3 + 3x^2 – 1) \\ &= -3x^2 + 6x \\ &= -3x (x – 2) \end{align*} |
and
| \begin{align*} \frac{d^2 y}{dx^2} & = \frac{d}{dx} (-3x^2 + 6x) \\ & = -6x + 6 \\ & = -6(x – 1) \end{align*} |
For the stationary points, setting \( \frac{dy}{dx} = 0 \) gives
| \( -3x (x – 2) = 0 \) |
so
| \begin{align*} x = 0 \quad \text{or} \quad x = 2. \end{align*} |
When \( x = 0 \),
| \begin{align*} y &= -0^3 + 3 (0)^2 – 1 \\ &= -1 \end{align*} |
When \( x = 2 \)
| \begin{align*} y &= -2^3 + 3(2)^2 – 1 \\ &= 3 \end{align*} |
Therefore, the stationary points are \( (0,-1) \) and \( (2, 3) \).
| \( x \) | \( x < 0 \) | \( x = 0 \) | \( 0 < x < 2 \) | \( x = 2 \) | \( x > 2 \) |
| \( \frac{dy}{dx} \) | \( – \) | \( 0 \) | \( + \) | \( 0 \) | \( – \) |
For the points of inflection, setting \( \frac{d^2 y}{dx^2} = 0 \) gives
| \begin{align*} -6(x – 1) = 0 \end{align*} |
So,
| \begin{align*} x = 1 \end{align*} |
When \( x = 1 \),
| \begin{align*} y &= -1^3 + 3(1)^2 – 1 \\ &= 1 \end{align*} |
Therefore, the point of inflection is \( (1,1) \).
| \( x \) | \( x < 1 \) | \( x = 0 \) | \( x > 1 \) |
| \( \frac{d^{2}y}{dx^{2}} \) | \( + \) | \( 0 \) | \( – \) |
The \( y \) -intercept is
| \begin{align*} y &= -0^3 + 3(0)^2 – 1 \\ &= -1 \end{align*} |
We use integration by substitution. Let \( u = 4 + x^2 \). Then \( \frac{du}{dx} = 2x \), so \( du = 2x \ dx \).
Therefore,
| \begin{align*} \int \frac{x}{4 + x^2} \, dx &= \int \frac{1}{2} \left(\frac{2x}{4 + x^2}\right) \, dx \\ &= \int \frac{1}{2} \left(\frac{du}{u}\right) \\ &= \frac{1}{2} \ln \left|u\right| + C \\ &= \frac{1}{2} \ln \left|4 + x^2\right| + C \\ &= \frac{1}{2} \ln \left(4 + x^2\right) + C \,, \quad \text{since $4 + x^2 > 0$} \,, \end{align*} |
Where \( C \) is a constant.
Using the product rule gives
| \begin{align*} \frac{d}{dx} \left(e^{2x} \left(2x + 1\right)\right) &= e^{2x} \frac{d}{dx} \left(2x + 1\right) + \left(2x + 1\right) \frac{d}{dx} \left(e^{2x}\right) \\ &= e^{2x} \left(2\right) + \left(2x + 1\right) \left(2e^{2x}\right) \\ &= 2e^{2x} + 4xe^{2x} + 2e^{2x} \\ &= 4e^{2x} + 4xe^{2x} \\ &= 4e^{2x} \left(1 + x\right) \,. \end{align*} |
We have
| \begin{align*} \int \left(x + 1\right) e^{2x} \, dx &= \frac{1}{4} \int 4 \left(x + 1\right) e^{2x} \, dx \\ &= \frac{1}{4} \left[e^{2x} \left(2x + 1\right)\right] + C \,, \end{align*} |
where \( C \) is a constant, using the result from part (a).
Starting from the left hand side, we have
| \begin{align*} \sec \theta – \cos \theta &= \frac{1}{\cos \theta} – \cos \theta \\ &= \frac{1 – \cos^2 \theta}{\cos \theta} \\ &= \frac{\sin^2 \theta}{\cos \theta} \\ &= \sin \theta \cdot \frac{\sin \theta}{\cos \theta} \\ &= \sin \theta \tan \theta \end{align*} |
as required.
Using the trapezoidal rule, we find that
| \begin{align*} \text{approximate distance} &= \frac{\frac{1}{60}}{2} \left[60 + 2 \left(55 + 65 + 68 + 70\right) + 67\right] \\ &= \frac{643}{120} \\ &= 5.358\\ &=5.4 \ (1\text{ d.p.})\\ \end{align*} |
The temperate of the tea 4 minutes after it has been poured is found by substituting \( t = 4 \) into \( T \) , which gives
| \begin{align*} T &= 25 + 70 \left(1.5\right)^{-0.4 \left(4\right)} \\ &= 25 + 70 \left(1.5\right)^{-0.4 \left(4\right)} \\ &= 25 + 70\left(1.5\right)^{-1.6} \\ &\approx 61.5891 \text{degrees Celsius.} \end{align*} |
The rate of change of the temperature of the tea is
| \begin{align*} \frac{dT}{dt} &= \frac{d}{dt} \left(25 + 70\left(1.5\right)^{-0.4t}\right) \\ &= 70\left(1.5\right)^{-0.4t} \left(\log_e 1.5\right) \frac{d}{dt} \left(-0.4t\right) \\ &= 70\left(1.5\right)^{-0.4t} \left(\log_e 1.5\right) \left(-0.4\right) \\ &= \left(-28\log_e 1.5\right) \left(1.5\right)^{-0.4t} \,. \end{align*} |
When \( t = 4 \) , this becomes
| \begin{align*} \frac{dT}{dt} &= \left(-28\log_e 1.5\right) \left(1.5\right)^{-0.4 \left(4\right)} \\ &\approx -5.93425 \,, \end{align*} |
which is negative, so the tea is cooling at the rate of \( 5.93425 \) degrees Celsius per minute.
Substituting \( T = 55 \) into \( T = 25 + 70 (1.5)^{-0.4t} \) gives
| \begin{equation*} 55 = 25 + 70 \left(1.5\right)^{-0.4t} \,, \end{equation*} |
so
| \begin{equation*} 30 = 70 \left(1.5\right)^{-0.4t} \,, \end{equation*} |
and
| \begin{equation*} \frac{3}{7} = \left(1.5\right)^{-0.4t} \,. \end{equation*} |
Taking logarithms on both sides of the equation gives
| \begin{equation*} \log_e \left(\frac{3}{7}\right) = \log_e \left(1.5\right)^{-0.4t} \,, \end{equation*} |
so
| \begin{equation*} \log_e \left(\frac{3}{7}\right) = -0.4t \log_e \left(1.5\right) \,, \end{equation*} |
and
| \begin{align*} t &= -\frac{1}{0.4 \log_e \left(1.5\right)} \log_e \left(\frac{3}{7}\right) \\ &\approx 5.22423 \end{align*} |
Using the given perimeter we have
| \begin{align*} AB &= \frac{\text{perimeter}}{\text{number of sides}} \\ &= \frac{80}{10} \\ &= 8 \, \textrm{cm} \end{align*} |
We also have
| \begin{align*} \angle AOB &= 360° \div 10 \\ &= 36° \end{align*} |
Using the cosine rule gives
| \( AB^2 = AO^2 + BO^2 – 2 \times AO \times BO \times \cos \angle AOB \) |
Since \( AO = BO \) and \( AB = 8 \), we have
| \begin{align*} 8^2 &= AO^2 + AO^2 – 2 \times AO \times AO \times \cos 36° \\ 64 &= 2 (AO)^2 – 2 AO^2 \cos 36° \\ 64 &= AO^2 (2 – 2 \cos 36°) \\ AO^2 &= \frac{64}{2 – 2 \cos 36°} \end{align*} |
Therefore,
| \begin{align*} \text{area of the decagon} &= 10 \times \text{area of} \triangle \text{AOB} \\ &= 10 \times \left[\frac{1}{2} \times AO^2 \sin 36º \right] \\ &= 10 \times \frac{1}{2} \times \frac{64}{2 – 2 \cos 36º} \times \sin 36º \\ &= 492.429 \\ &\approx 492.4 \, \textrm{cm}^2 \quad \text{(correct to 1 d.p.)} \end{align*} |
Since \( f(x) \) is a probability density function, we know that
| \begin{align*} \int_0^k \sin x \, dx &= 1 \\ \left[-\cos x\right]_0^k &= 1 \\ – \cos k – \left(- \cos 0\right) &= 1 \\ – \cos k + 1 &= 1 \\ \cos k &= 0 \, \end{align*} |
Solving this for \( k \) gives
| \( k = \frac{\pi}{2} \) |
Since \( 1 < \frac{\pi}{2} \), we have
| \begin{align*} P\left(X \leq 1\right) &= \int_0^1 f\left(x\right) \, dx \\ &= \int_0^1 \sin x \, dx \\ &= \left[-\cos x\right]_0^1 \\ &= -\cos 1 – \left(- \cos 0\right) \\ &= – \cos 1 + 1 \\ &= 0.4597 \,. \end{align*} |
Starting with the circle given, we complete the square and obtain
| \begin{align*} x^2 – 6x + y^2 + 4y – 3 &= 0 \\ x^2 – 6x + y^2 + 4y &= 3 \\ \left(x^2 – 6x + 9\right) + \left(y^2 + 4y + 4\right) &= 3 + 9 + 4 \\ \left(x – 3\right)^2 + \left(y + 2\right)^2 &= 16 \ \end{align*} |
This means that the original circle is centred at \( (3, -2) \) and its radius is \( 4 \) units.
When it is reflected in the \( x \) -axis, we multiply the \( y \) -coordinate by \( -1 \) so the centre of the reflected circle is \( (3,2) \) , and the radius is still \( 4 \) units.
The radius of the quarter circle is \( x \) metres. We have
| \begin{align*} \text{area of garden bed} &= \text{area of rectangle} + \text{area of quarter circle} \\ &= xy + \frac{1}{4} \left(\pi x^2\right) \,. \end{align*} |
Since this has to be equal to \( 36 \), we have
| \begin{align*} xy + \frac{1}{4} \left(\pi x^2\right) &= 36 \\ xy &= 36 – \tfrac{1}{4} \left(\pi x^2\right) \\ y &= \frac{36}{x} – \frac{\pi x}{4} \,. \end{align*} |
Therefore, the perimeter is given by
| \begin{align*} P &= x + y + \left(x + y\right) + \frac{1}{4} \left(2 \pi x\right) \\ &= 2 \left(x + y\right) + \frac{\pi x}{2} \\ &= 2 \left[x + \left(\frac{36}{x} – \frac{\pi x}{4}\right)\right] + \frac{\pi x}{2} \\ &= 2x + \frac{72}{x} – \frac{\pi x}{2} + \frac{\pi x}{2} \\ &= 2x + \frac{72}{x} \,, \end{align*} |
as required.
First, we differentiate \( P = 2x + \frac{72}{x}\) and obtain
| \begin{align*} \frac{dP}{dx} &= \frac{d}{dx} \left(2x + \frac{72}{x}\right) \\ &= 2 – \frac{72}{x^2} \,. \end{align*} |
Setting \( \frac{dP}{dx} = 0 \) gives \( 2 – \frac{72}{x^2} = 0 \). This means that
| \( \frac{72}{x^2} = 2 \) |
so
| \( x^2 = 36 \) |
and
| \( x = 6 \) |
since \( x \) is the dimension of a rectangle and it must be non-negative. When \( x = 6 \), the perimeter is given by
| \begin{align*} P &= 2 \left(6\right) + \frac{72}{6} \\ &= 12 + 12 \\ &= 24 \ \text{metres} \end{align*} |
| \( x \) | \( 0 < x < 6 \) | \( x = 6 \) | \( x > 6 \) |
| \( \frac{dP}{dx} \) | \( – \) | \( 0 \) | \( + \) |
Therefore, \( P = 24 \) is the smallest possible perimeter.
We use the recurrence relation starting with
| \( A_0 = 60000 \) |
The amount of money in the account after the first withdrawal is
| \begin{align*} A_1 &= A_0 \left(1.005\right) – 800 \\ &= 60000 \left(1.005\right) – 800 \,, \end{align*} |
The amount of money in the account after the second withdrawal is
| \begin{align*} A_2 &= A_1 \left(1.005\right) – 800 \\ &= \left[60000 \left(1.005\right) – 800\right] \left(1.005\right) – 800 \\ &= 60000 \left(1.005\right)^2 – 800 \left(1 + 1.005\right) \,, \end{align*} |
And the amount of money in the account after the third withdrawal is
| \begin{align*} A_3 &= A_2 \left(1.005\right) – 800 \\ &= \left[60000 \left(1.005\right)^2 – 800 \left(1 + 1.005\right)\right] \left(1.005\right) – 800 \\ &= 60000 \left(1.005\right)^3 – 800 \left(1 + 1.005 + 1.005^2\right) \\ &\approx 58492.49 \quad \text{(correct to 2 d.p.)} \,. \end{align*} |
The interest in the first month is
| \begin{align*} I_1 &= A_0 \times 0.5\% \\ &= 60000 \times 0.005 \\ &= \$ 300 \end{align*} |
The interest in the second month is
| \begin{align*} I_2 &= A_1 \times 0.5\% \\ &= \left(60000 \times 1.005 – 800\right) \times 0.005 \\ &= \$ 297.50 \end{align*} |
The interest in the third month is
| \begin{align*} I_3 &= A_2 \times 0.5\% \\ &= \left(60000 \times 1.005^2 – 800 \times 1.005 – 800\right) \times 0.005 \\ &= \$ 294.99 \end{align*} |
Therefore, the total amount of interest earned in the first three months is
| \begin{align*} I_1 + I_2 + I_3 &= \$ 892.49 \end{align*} |
The amount of money in the account immediately after the 94th withdrawal is
| \begin{align*} A_{94} &= A_{93} \left(1.005\right) – 800 \\ &= 60000 \times 1.005^{94} – 800 \times \left(1 + 1.005 + 1.005^2 + \dots + 1.005^{93}\right) \\ &= 60000 \times 1.005^{94} – 800 \times \left(\frac{1 – 1.005^{94}}{1 – 1.005}\right) \\ &= \$ 187.85 \quad \text{correct to 2 decimal places} \end{align*} |
From the box plot, the median of the temperature is \( 22 \) degrees Celsius. It is given that the mean temperature is \( 0.525 \) degrees below the median temperature, so
| \begin{align*} \bar{x} &= 22 – 0.525 \\ &= 21.475 \ \text{degrees Celsius} \end{align*} |
The average number of chirps over the 20 days is
| \begin{align*} \bar{y} &= \frac{684}{20} \\ &= 34.2 \end{align*} |
Taking the expected value of both sides of
| \(y = -10.6063 + bx \) |
gives
| \(\bar{y} = -10.6063 + b \bar{x} \) |
so
| \( 34.2 = -10.6063 + b \left(21.475\right) \) |
and
| \begin{align*} b &= \frac{34.2 + 10.6063}{21.475} \\ &= 2.08644004657 \end{align*} |
This means that
| \( y = -10.6063 + 2.08644004657x \) |
Therefore, the number of chirps expected in a 15-second interval when the temperature is 19 degrees Celsius is found by substituting \( x = 19 \), giving
| \begin{align*} y &= -10.6063 + 2.08644004657 \left(19\right) \\ &\approx 29 \quad \text{(correct to the nearest whole number)} \,. \end{align*} |
Let \( X \) dollars be the hourly rate of pay for adults who work. We are given that \( X \sim \mathcal{N} \left(25, 5^2\right) \) , so the probability that an adult earns between \( \$ 15 \) and \( \$30 \) per hour is
| \begin{align*} P\left(15 \leq X \leq 30\right) &= P\left(\frac{15 – 25}{5} \leq \frac{X – 25}{5} \leq \frac{30 – 25}{5}\right) \\ &= P\left(-2 \leq Z \leq 1\right) \\ &= 0.84134 – 0.02275 \\ &= 0.81859 \end{align*} |
Therefore,
| \begin{align*} P\left(\text{an adult’s hourly rate of pay is not between \$15 and \$30}\right) &= 1 – P\left(15 \leq X \leq 30\right) \\ &= 1 – 0.81859 \\ &= 0.18141 \end{align*} |
and
| \begin{align*} P\left(\text{at least one of two adults earns between \$15 and \$30}\right) &= 1 – P\left(\text{neither earns between \$15 and \$30 an hour}\right) \\ &= 1 – 0.18141^2 \\ &= 0.9671 \end{align*} |
Since the number of adults who work is equal to three times the number of adults who do not work, we know that
| \begin{equation*} P \left(\text{a randomly chosen adult works}\right) = \frac{1}{4} \end{equation*} |
This means that
| \begin{align*} &∴P \left( \text{Chosen adult works and earns more than}\ \$25 \text{ per hour} \right) = \frac{3}{4} \times \frac{1}{2} \\ & =\frac{3}{8} \end{align*} |
Since
| \begin{align*} \frac{dy}{dx} &= \frac{d}{dx} \left(c \ln x\right) \\ &= \frac{c}{x} \,, \end{align*} |
the slope of the tangent to \( y = c \ln x \) at \( x = p \) is
| \(\frac{dy}{dx}\bigg|_{x = p} = \frac{c}{p} \) |
When \( x = p \), the corresponding \( y \)-coordinate is
| \begin{equation*} y = c \ln p \\ \end{equation*} |
This means that the equation of the tangent to \( y = c \ln x \) at \( x = p \) is given by
| \begin{equation*} \frac{y – c \ln p}{x – p} = \frac{c}{p} \end{equation*} |
Multiplying both sides by \( x – p \) gives \( y – c \ln p = \frac{c}{p} \left(x – p\right) \), so
| \begin{align*} y &= \frac{c}{p} \left(x – p\right) + c \ln p \\ &= \frac{c}{p} x – c + c \ln p \,, \end{align*} |
as required.
Since the tangent has a gradient of \( 1 \), we have
| \begin{equation} \label{eq:Q29bEq1} \frac{c}{p} = 1 \end{equation} |
which means that
| \begin{equation} \label{eq:Q29bEq2} c = p \end{equation} |
Furthermore, since the tangent passes through the origin, substituting \( x = 0 \) and \( y = 0 \) into the equation of the tangent gives
| \begin{equation*} 0 = \frac{c}{p} \left(0\right) – c + c \ln p \end{equation*} |
which means that \( 0 = -c + c \ln p \), or equivalently,
| \begin{equation} \label{eq:Q29bEq3} c \left(-1 + \ln p\right) = 0 \end{equation} |
From Eq. \( \frac{c}{p} = 1\), we know that \( c \neq 0 \), so Eq. \( c \left(-1 + \ln p\right) = 0 \) implies that
| \begin{equation*} -1 + \ln p = 0 \,, \end{equation*} |
which means that
| \begin{equation*} \ln p = 1 \,, \end{equation*} |
and
| \begin{equation} \label{eq:Q29bEq4} p = e \ \end{equation} |
Substituting \( p = e \) into \( c = p \) gives
| \begin{equation*} c = e \,. \end{equation*} |
Since \( A \) is the point of intersection of
| \begin{equation*} y = 4x – x^2 \end{equation*} |
and
| \begin{equation*} y = ax^2 \end{equation*} |
its \( x \) -coordinate is found by equating both equations and solving for \( x \). This gives
| \begin{equation*} 4x – x^2 = ax^2 \end{equation*} |
so
| \begin{equation*} \left(1 + a\right) x^2 – 4x = 0 \end{equation*} |
or equivalently,
| \begin{equation*} x \left [ \left(1 + a \right )x – 4 \right] = 0 \end{equation*} |
Either \( x = 0 \) or \( \left(1 + a\right) x – 4 = 0 \), but from the diagram we see that the \( x \) coordinate of \( A \) is not \( 0 \), which means that we must have
| \begin{equation*} \left(1 + a\right) x – 4 = 0 \end{equation*} |
Rearranging this gives
| \begin{equation*} \left(1 + a\right) x = 4 \end{equation*} |
so
| \begin{equation*} x = \frac{4}{1 + a} \end{equation*} |
as required.
The shaded area is given by
| \begin{align*} \int_0^{4/\left(1+a\right)} \left[\left(4x – x^2\right) – ax^2\right] \, dx &= \int_0^{4/\left(1+a\right)} \left[\left(4x – x^2\right) – ax^2\right] \, dx \\ &= \int_0^{4/\left(1+a\right)} \left(4x – x^2 – ax^2\right) \, dx \\ &= \left[2x^2 – \frac{x^3}{3} – \frac{ax^3}{3}\right]_0^{4/\left(1+a\right)} \\ &= 2\left(\frac{4}{1 + a}\right)^2 – \frac{1}{3} \left(\frac{4}{1 + a}\right)^3 – \frac{a}{3} \left(\frac{4}{1 + a}\right)^3 \\ &= \frac{32}{\left(1 + a\right)^2} – \frac{64}{3 \left(1 + a\right)^3} – \frac{64a}{3\left(1 + a\right)^3} \\ &= \frac{96 \left(1 + a\right) – 64 -64a}{3\left(1 + a\right)^3} \\ &= \frac{96 + 96a – 64 -64a}{3\left(1 + a\right)^3} \\ &= \frac{32 \left(1 + a\right)}{3\left(1 + a\right)^3} \\ &= \frac{32}{3\left(1 + a\right)^2} \end{align*} |
Therefore, in order for the shaded area to be equal to \( \frac{16}{3} \), we need
| \begin{equation*} \frac{32}{3\left(1 + a\right)^2} = \frac{16}{3} \end{equation*} |
which means
| \begin{equation*} \left(1 + a\right)^2 = 2 \end{equation*} |
Therefore,
| \begin{equation*} 1 + a = \pm \sqrt{2} \end{equation*} |
so \( a = -1 \pm \sqrt{2} \). From the diagram, we need \( a > 0 \), so
| \begin{equation*} a = -1 + \sqrt{2} \end{equation*} |
\( a \) represents the amplitude, so
| \begin{align*} a &= \frac{35000 – 5000}{2} \\ &= 15000 \end{align*} |
\( b \) represents the vertical displacement, so
| \begin{align*} b &= 35000 – 15000 \\ &= 20000 \end{align*} |
Differentiating \( m\left(t\right) \) gives
| \begin{equation*} m’\left(t\right) = 15000\left(\frac{\pi}{26}\right) \cos \left(\frac{\pi}{26} t\right) \end{equation*} |
For \( m\left(t\right) \) to be increasing, we assess when \( m’\left(t\right) > 0 \). This occurs when
| \begin{equation*} \cos \left(\frac{\pi}{26} t\right) > 0 \end{equation*} |
So
| \begin{equation*} \frac{\pi}{26} t < \frac{\pi}{2} \quad \text{or} \quad \frac{\pi}{26} t > \frac{3 \pi}{2} \end{equation*} |
This means that
| \begin{equation*} t < 13 \quad \text{or} \quad t > 39 \end{equation*} |
Likewise with \( c\left(t\right) \), and we have
| \begin{equation*} c’\left(t\right) = \frac{80 \pi}{26} \sin \left[\frac{\pi}{26} \left(t – 10\right)\right] \end{equation*} |
Now, \( c’\left(t\right) > 0 \) occurs when
| \begin{equation*} \sin \left[\frac{\pi}{26} \left(t – 10\right)\right] > 0 \end{equation*} |
which means that
| \begin{equation*} 0 < \frac{\pi}{26} \left(t – 10\right) < \pi \end{equation*} |
so
| \begin{equation*} 10 < t < 36 \end{equation*} |
Therefore, both populations are increasing when
| \begin{equation*} 10 < t < 13 \end{equation*} |
First, we find when \( c\left(t\right) \) reaches a maximum. This occurs when \( c’\left(t\right) = 0 \), so
| \begin{equation*} \frac{80 \pi}{26} \sin \left[\frac{\pi}{26} \left(t – 10\right)\right] = 0 \,, \end{equation*} |
or equivalently,
| \begin{equation*} \sin \left[\frac{\pi}{26} \left(t – 10\right)\right] = 0 \,. \end{equation*} |
Therefore,
| \begin{equation*} \frac{\pi}{26} \left(t – 10\right) = 0 \quad \text{or} \quad \frac{\pi}{26} \left(t – 10\right) = \pi \,, \end{equation*} |
and the stationary points are
| \begin{equation*} t = 10 \quad \text{or} \quad t = 36 \,. \end{equation*} |
To determine the nature of these stationary points, we examine \( c”\left(t\right) \). Now,
| \begin{equation*} c”\left(t\right) = \frac{80 \pi^2}{26^2} \cos \left(\frac{\pi}{26} \left(t – 10\right)\right) \,. \end{equation*} |
At \( t = 36 \),
| \begin{align*} c”\left(36\right) &= -1.168 \\ &< 0 \end{align*} |
so \( c\left(t\right) \) attains its maximum when \( t = 36 \). At \(t = 36 \) ,
| \begin{align*} m’\left(36\right) &= \frac{15000\pi}{26} \cos \left(\frac{36 \pi}{26}\right) \\ &= -642.7\\ \end{align*} |
Use the calculator to explore the HSC Marks you need to achieve your ATAR Goal.
Written by Matrix Maths Team
The Matrix Maths Team are tutors and teachers with a passion for Mathematics and a dedication to seeing Matrix Students achieving their academic goals.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
