Module 2: Dynamics | Beginner’s Guide to Year 11 Physics

Do your Year 11 Physics marks need a bit of a push? Don’t worry! In this Guide, we’re going to give you an overview of Year 11 Dynamics so you can give your results the boost they need!

Change the Dynamics of your Physics scores for the better

Year 11 Dynamics

In this article, we’ll look at the following Dynamics topics:

• What is Dynamics?
• Forces and Newton’s Laws
• Work, Energy, and Power
• Momentum and Impulse

What is Dynamics?

In Module 1 you studied Kinematics: the description of motion without any consideration of what caused or changed the motion. Dynamics represents the other half of mechanics, where we will learn how forces lead to and affect motion and analyse interactions between objects.

There are a number of new concepts, quantities and relationships in this topic. Make sure that you understand the definitions of each one as well as the equations that connect them.

Dynamics Topic 1: Forces and Newton’s Laws

Perhaps Isaac Newton’s greatest contribution to science was his formulation of classical mechanics. He took a wide range of physical observations and showed that they could be accounted for through three fundamental laws:

1. An object remains at rest or moves with constant velocity unless acted upon by a net external force.
2. The acceleration of an object is equal to the net external force on the object divided by the mass of the object: \(\vec{a}=\frac{\vec{F}_{net}}{m}\)
3. For every action force, there is an equal and opposite reaction force.

You will recognize some of the terms used in the laws from Kinematics – velocity and acceleration. Newton argued that acceleration could only occur as the result of a nonzero net force on a mass. So what is a force?

A force is any push or pull acting on an object, and it is measured in units of newtons (N). Some are easy to identify, such as the force your hands apply to a ball when you throw it. Other examples of forces are friction and air resistance, or even the invisible force of gravity pulling you back to the surface of the Earth when you jump. Regardless of what type of force is involved, Newton’s three laws are always true.

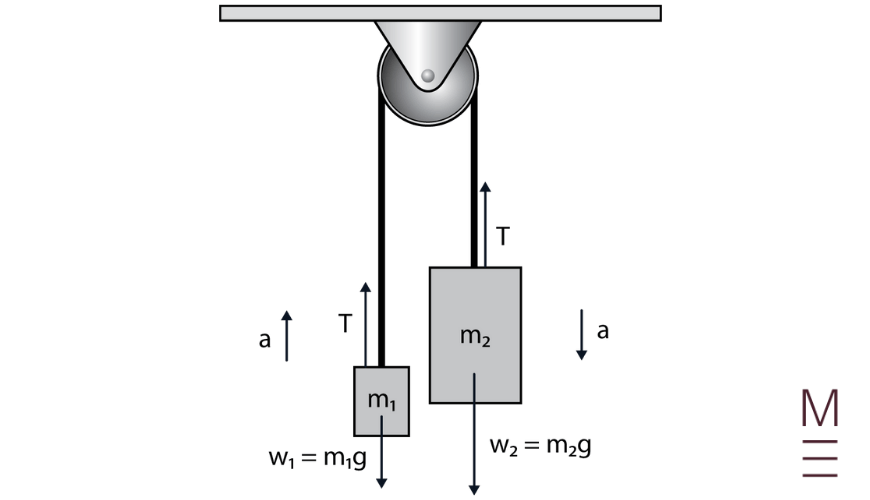
When you study Dynamics, you will look at what happens when forces are applied to single objects, or even complex systems of objects like the Atwood machine pictured here.

Two forces which we can calculate using equations are weight and friction.

Weight is the force exerted on an object due to the Earth’s gravity, and is given by \(w=mg\). The \(g\) represents the strength of the gravitational field and is equal to \(9.8 \text{ Nkg}^{-1}\).

The amount of friction experienced by an object depends on the surfaces involved and how hard the object is pressing down onto that surface. The friction force is \(F=μN\), where \(μ\) is called the coefficient of friction and \(N\) is the normal force. Friction will be static if the object is not moving, keeping the object in place against an applied force. If the object is moving it will experience kinetic friction which resists the object’s motion. Often the coefficient of friction will be different for these two types.

Dynamics Topic 2: Work, energy and power

Once we understand forces, we can start using the related concept of work. In Physics, work is done when a force is applied over some displacement. It is calculated by the formula \(W=Fs \cos⁡θ\), where \(θ\) is the angle between the force vector and the displacement vector, and the units are joules (J). Because of the \(\cos⁡θ\) dependence, work can be positive, zero or negative depending on the directions of the vectors.

The effect of doing work is to transfer energy from one place to another or one form to another. Doing positive work on an object increases its energy, whereas negative work decreases its energy.

You will know some of the basics of energy from Junior Science. In particular, you will have learned about conservation of energy: it can be transferred between objects or into different forms, but never created or destroyed. In Year 11, we say that energy is the ability to do work.

Work and energy are tied together by the work-energy principle, which allows us to determine the relationship between forces on an object and the energy gained or lost.

The two types of energy we focus on in this Module are kinetic and gravitational potential energy.

Kinetic energy \(K=\frac{1}{2} mv^2\) is the energy an object has due to its motion.

Gravitational potential energy \(U=mgh\) is the energy an object has due to its position in a gravitational field.

Gravity itself can do work on an object, or an external force can do work against gravity. When gravity does work, any losses in potential energy are converted to kinetic energy and vice versa.

One more related concept is power measured in watts (joules per second). This is the rate at which work is done (or energy changes) over time.

Doing the same task more slowly requires less power.

Dynamics Topic 3: Momentum and impulse

A moving object has a quantity called momentum, calculated by \(\vec{p}=m\vec{v}\). This is a measure of how difficult it would be to bring the object to a stop. Revisiting Newton’s First Law, we can say that an object’s momentum stays the same unless it is acted upon by a net external force. Note that it is a vector quantity – direction matters!

The product of the force and the time over which it is applied is called the impulse, \(I = F\Delta t\), and this quantity is equal to the change in momentum.

This course has mostly dealt with single objects experiencing forces and occasionally connected objects with internal forces. The concepts of momentum and impulse allow us to expand our understanding to collisions – interactions where two objects apply forces to each other for brief periods of time, changing the motion of both.

When two objects A and B collide, the forces they apply to each other are equal and opposite – a consequence of Newton’s Third Law. As a result, while A and B will both experience a change in momentum, their total momentum will stay the same before and after the collision! If we use the convention that \(\vec{u}\) represents initial velocity and \(\vec{v}\) represents final velocity, then:

A collision may be elastic, in which case kinetic energy is also conserved, or inelastic, in which case some kinetic energy is converted to other forms such as heat and sound.

Need to get the momentum back in your Physics marks?

Matrix Year 11 Physics Term Courses have a proven track record of improving student’s results. Learn more!