Select a year to see courses
Prior to learning about Volume and Capacity, you would have explored length and area, including converting between different units of measurements and finding the area of a variety of 2D shapes.
Improve your knowledge and skills of Volume and Capacity
Practise and develop your Maths skills with this free worksheet.
Volume and Capacity is an extension of these topics, and I guess you could say there is more depth to this topic.
Volumes and Capacity is a fundamental concept that you will evidently explore further in senior mathematics.
We hope that this guide allows you to gain a deeper understanding of three-dimensional solids.
| Syllabus | Explanation |
| Stage 4 NSW Syllabus | |
| Draw different views of prisms and solids formed from combinations of prisms (ACMMG16) | Distinguish between solids with uniform and non-uniform cross-sections |
| Choose appropriate units of measurement for volume and convert from one unit to another (ACMMG195) | Convert between metric units of volume and capacity, using:
|
| Develop the formulas for the volumes of rectangular and triangular prisms and of prisms in general; use formulas to solve problems involving volume (ACMMG198) |
|
| Calculate the volumes of cylinders and solve related problems (ACMMG217) |
|
Students would have been exposed to length and area in Stage 4 as a prerequisite to exploring volume and capacity.
Students should be able to convert between different units of length.
e.g. Between \( km\) to \(cm\), and should be able to determine the areas of some quadrilaterals, triangles and circles.
Previously you would have learnt about area in our Beginner’s Guide to Year 7 Maths: Part 6: Area.
Remember, area is the amount of space inside the boundary of a two-dimensional object such as squares and circles.
When we introduce a third dimension, known as depth, we have three-dimensional objects such as cubes and triangular prisms.
Volume is the amount of space occupied by a three-dimensional solid.
Recall that when we convert between one-dimension lengths we use the following conversion chart.
Now, let’s consider a cube with dimensions of \(1m\).
The volume of the above solid, using \( V = Ah \) is:
\begin{align*}
V \ = \ 1m \times 1m \times 1m = 1m^{3}
\end{align*}
Now, using the conversion table above, what if we converted the units to centimetres instead?
Using \( V = Ah \) we find that the volume of the solid is:
\begin{align*}
V = 100cm \times 100cm \times 100cm = 1 \ 000 \ 000 cm^3
\end{align*}
However, these cubes are the same cube.
So, we can say that:
\begin{align*}
1m^3 = 1 \ 000 \ 000 cm^3
\end{align*}
Using the same reasoning, we can say that:
\begin{align*}
1cm^3 = 10mm \times 10mm \times 10mm = 1 \ 000cm^3
\end{align*}
We can refer to the following conversion chart below.
Note, that this chart is exactly the same as the above chart except we cube each unit and quantity.
Convert each of the following units for volume.
1. \( 325cm^3 \ \text{to} \ mm^3 \)
Solution:
\begin{align*}
325cm^3 &= 325 \times 10^3 \\
&= 325 \ 000 mm^3
\end{align*}
\( ( \times \ 10^3 \ \text{to convert from} \ cm^3 \ \text{to} \ mm^3 ) \)
2. \( 12.4mm^3 \ to \ cm^3 \)
Solution:
\begin{align*}
12.4 mm^3 &= 12.3 \div 10^3 \\
&= 0.0124cm^3
\end{align*}
\( (\div 10^{3} \ \text{to convert from} \ mm^3 \ \text{to} \ cm^3 \)
3. \( 0.0083m ^3 \ \text{to} \ mm^3 \)
Solution:
\begin{align*}
0.0083m^3 &= 0.0083 \times 100^3 \times 10^3
\end{align*}
\( (\times 100^3 \ \text{to convert from} \ \ m^3 \ \text{to} \ cm^3) \)
\begin{align*}
&= 8 \ 300 \ 000mm^3
\end{align*}
\( (\times 10^3 \text{to convert from} \ cm^3 \ \text{to} \ mm^3 \)
A prism is a solid that has identical polygon ends and the same cross-section across its entire length.
In other words, if you were to slice a prism along its height, the cross-sectional faces would be identical polygons.
Each prism has two congruent faces (ends), and the height of a prism is defined as the distance between these congruent faces.
 |
|
 |
|
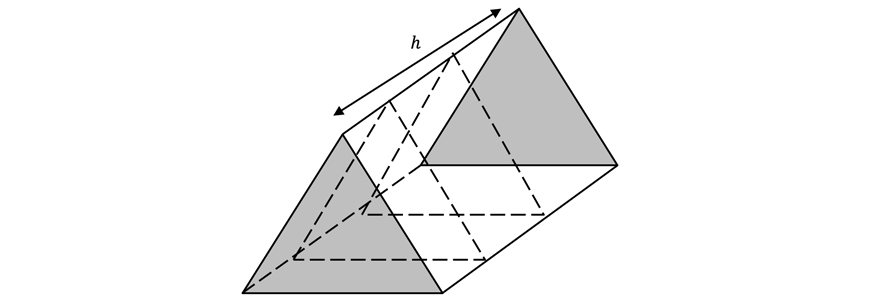Learn about Volume and Capacity and other Year 8 Maths topics before it’s taught in school! Learn more about our Year 8 Maths Course.
The formula for calculating the volume of a prism is:
\begin{align*}
V \ = \ Ah
\end{align*}
Where:
The table below summarises the area of the two-dimensional shapes that you will need to know.
| Name | Shape | Formula |
| Rectangle | 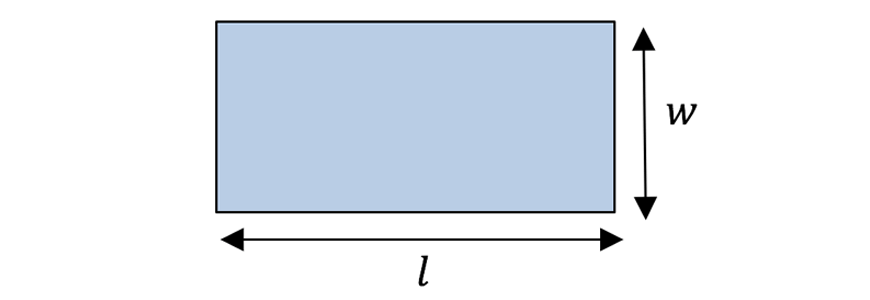 | \begin{align*} A &= lw \\ l &= length \\ w &= width \end{align*} |
| Square | 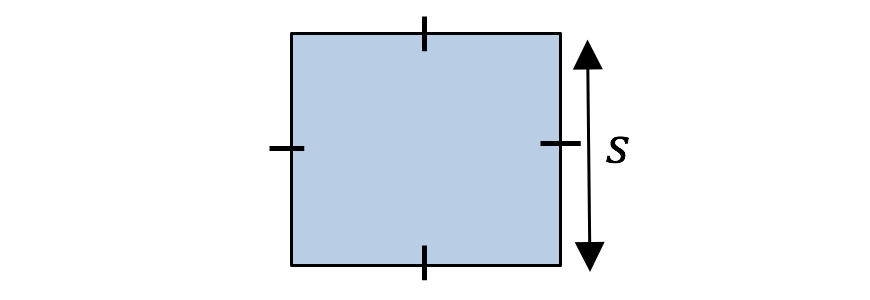 | \begin{align*} A &= s^2 \\ s &= side \ length \end{align*} |
| Triangle | 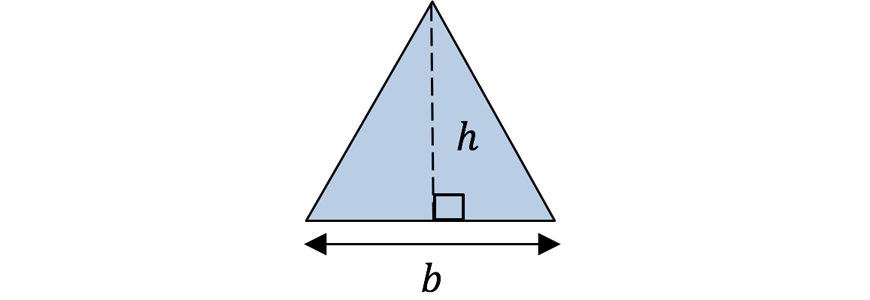 | \begin{align*} A &= \frac{1}{2}bh \\ b &= base \ length \\ h &= perpendicular \ height \end{align*} |
| Trapezium | 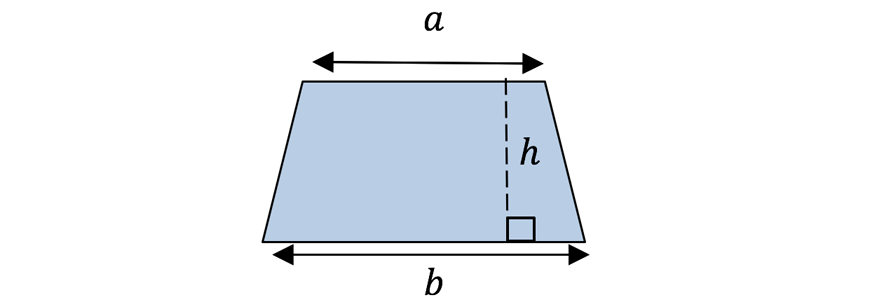 | \begin{align*} A &= \frac{h}{2}(a + b) \\ h &= perpendicular \ height \\ a &= length \ of \ 1st \ parallel \ side \\ b &= length \ of \ 2nd \ parallel \ side \end{align*} |
| Circle | 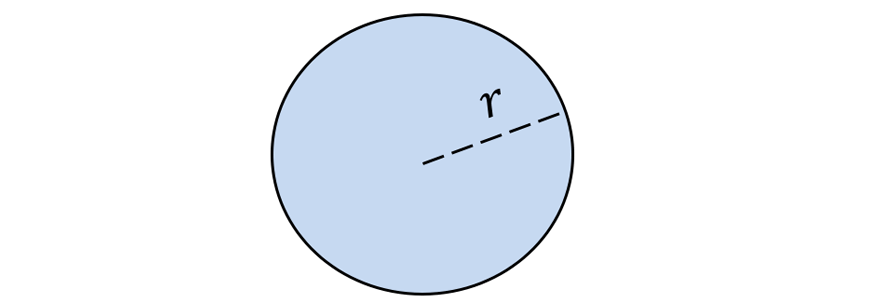 | \begin{align*} A &= \pi r^2 \\ r &= radius \ of \ circle \end{align*} |
1. Find the volume of the following prism correct to the nearest \( cm^3 \).
| Solution | Explanation |
| \begin{align*} A &= \frac{1}{2}bh \\ &= \frac{1}{2} \times 8 \times 12 \\ ∴ A &= 48cm^2 \\ V &= Ah \\ &= 48 \times 25 \\ ∴ V &= 1200 cm^3 \end{align*} | Triangle is the cross-section so we use \( A = \frac{1}{2}bh \) to find the area, where \( b = 12 \) and \( h = 8 \). By subbing in known values, we get \( A = 48cm^2 \). By inspection, the height of the prism is \( h = 25cm \) Hence, to find volume we use the formula: \begin{align*} |
2. Find the exact volume of the following prism
| Solution | Explanation |
| \begin{align*} A &= \frac{1}{2} \pi R^2 – \frac{1}{2} \pi r^2 \\ &= \frac{1}{2} \pi (R^2 – r^2) \\ &= \frac{1}{2} \pi (10^2 – 8^2) \\ &= \frac{1}{2} \pi \times 36 \\ ∴ A &= 18 \pi m^2 \\ V &= Ah \\ &= 18 \pi \times 12 \\ ∴ V &= 216 \pi m^3 \end{align*} | Let \( R \ = \ radius \) of larger semi-circle \begin{align*} \( r \ = \ radius \) of a smaller semi-circle \begin{align*} The cross section is half an annulus, or a larger semi-circle minus a smaller semi-circle. We then derive the area to be \( A = \frac{1}{2} \pi R^2 – \frac{1}{2} \pi r^2 = 18 \pi m^2 \) The height of the prism is \( h = 12m \). Hence to find the volume we use the formula: \begin{align*} |
Before we talk about conversions volume and capacity, we must first investigate how to convert between different units of capacity.
We will consider \( 3 \) main prefixes.
| Prefix | Magnitude | |
| Name | Symbol | |
| milli- | \( m \) | \( \frac{1}{1000} \times \) |
| kilo- | \( k \) | \( 1000 \times \) |
| mega- | \( M \) | \( 1 \ 000 \ 000 \times \) |
Note that the symbol is case-sensitive, do not use \( M \) when you mean milli and \( K \) when you mean kilo.
When we attach these prefixes in front of a unit, we change the magnitude of the unit.
To demonstrate by an example, a millilitre \( (mL) \) is \( \frac{1}{1000}th \) of a litre \( (L) \).
This is exactly like how when measuring length, a millimetre \( (mm) \) is \( \frac{1}{1000}th \) of a metre \( (m) \).
1. Convert \( 5L \)to \( mL \)
Since we want to convert from \( L \) to \( mL \).
Then by following the above flowchart, we have to multiply by \( 10^3 \) which is \( 1 \ 000 \).
\begin{align*}
5L &= 5 \times 1 \ 000 mL \\
&= 5 \ 000 mL
\end{align*}
2. Convert \( 780L \) to \( kL \)
Again, by following the flowchart, to convert from \( L \) to \( kL \) we must divide by \( 10^3 \).
\begin{align*}
780L &= 780 \div 1 \ 000 kL \\
&= 0.78 kL
\end{align*}
Sometimes, we have to perform more than one step through the flowchart when converting units.
3. Convert \(3.1 kL\) to \(mL \)
Notice that to get from \(kL \) to \(mL \), we have to multiply by \(10^3 \) twice. This is the same as saying multiplying by \(10^6 \).
\begin{align*}
3.1 \ kL \ &= \ 3.1 \times 1 \ 000 \ 000 \ mL \\
&= 3 \ 100 \ 000 mL
\end{align*}
The most basic conversion between units of volume and capacity is
\begin{align*}
1 \ cm^{3} = 1 \ mL
\end{align*}
We can convert any volume to capacity by the following steps:
1. Convert \( 26 \ kL \) to \( m^{3} \).
Solution:
Just like before, the above flowchart outlines the steps we have to take to solve this problem.
| Solution | Explanation |
| \begin{align*} 26 \ kL &= 26 \ 000 \ 000 \ mL \\ &= 26 \ 000 \ 000 \ cm^3 \\ &= 26 \ m^3 \end{align*} | \begin{align*} & \times 10^6 \ \text{to convert from} \ kL \ \text{to} \ mL\\ & \text{Rewrite} \ mL \ \text{as} \ cm^3 \\ & \div 10^{6} \ \text{to convert from} \ cm^3 \ \text{to} \ m^{3} \end{align*} |
Optional
If you are comfortable with converting from volumes to capacity using \(1 \ cm^3 = 1 \ mL \), we can do some questions faster if we know some more conversions
\begin{align*}
1 \ 000 \ cm^3 &= 1 \ L \\
1 \ m^3 &= 1 \ kL
\end{align*}
For the previous example where we converted from \(26 \ kL \) to \( m^3 \), we can do this in one step if we know the conversion \(1 \ m^3 = 1 \ kL \).
That is, \( 26 kL = 26m^3 \).
2. Convert \( 8.1m^3 \) to \( L \).
Solutions:
| Solution | Explanation |
| \begin{align*} 8.1 &= 8.1 kL \\ &= 8 \ 100 L \end{align*} | \begin{align*} & \text{Rewrite} \ m^3 \ \text{as} \ kL \ \text{since} \\ & 1m^3 = 1 kL \\ & \times 10^3 \ \text{to convert from} \ kL \ \text{to} \ L \end{align*} |
Calculating the capacity of some container is almost the same as calculating the volume of the container.
To calculate the capacity of a container:
1. Calculate the capacity of the following solid in \( L \).
Solution:
Step 1: Calculate the volume
Cross-sectional area is a right triangle, so we use formula for the area of a triangle.
\begin{align*}
A &= \frac{1}{2} \times 14m \times 5m \\
&= 35m^2
\end{align*}
Volume of triangular prism is
\begin{align*}
V &= A \times 20m \\
&= 35m^2 \times 20m \\
&= 700m^3
\end{align*}
Step 2: Convert the visual into capacity
We will do this by first converting to the units of volume to \( cm^3 \), then converting to capacity using \( 1cm^3 = 1mL \).
| Solutions | Explanation |
| \begin{align*} 700m^3 &= 700 \ 000 \ 000 \ cm^3 \\ &= 700 \ 000 \ 000 \ mL \\ &= 700 \ 000 \ L \end{align*} | \begin{align*} & \times 10^6 \ \text{to convert from} \ m^3 \ \text{to} \ cm^3 \\ & \text{Rewrite} \ cm^3 \ \text{as} \ mL \\ & \div 10^3 \ \text{to convert from} \ mL \ \text{to} \ L \end{align*} |
If you are feeling confident, feel free to use \( 1m^3 = 1kL \) to directly convert to capacity!
| Solutions | Explanation |
| \begin{align*} 700m^3 &= 700 kL \\ &= 700 \ 000 L \end{align*} | \begin{align*} & \text{Rewrite} \ m^3 \ \text{as} \ kL \\ & \times 10^3 \ \text{to convert from} \ kL \ \text{to} \ L \end{align*} |
2. Calculate the total capacity of water that this swimming pool can hold.
Solution:
Step 1: Calculate the volume
Observe that the cross-sectional area is the area of a trapezium.
So, we must use the formula for the area of a trapezium, which is \( A = \frac{a+b}{2} h \).
\begin{align*}
A &= \frac{1m + 1.8m}{2} \times 3.4m \\
&= 4.76 m^2
\end{align*}
So, the volume of the swimming pool is:
\begin{align*}
V &= A \times 10m \\
&= 4.76m^2 \times 10m \\
&= 47.6m^3
\end{align*}
Step 2: Convert the volume into capacity
| Solution | Explanation |
| \begin{align*} 47.6 \ m^3 &= 47.6 \ kL \\ &= 47 \ 600 \ L \end{align*} | \begin{align*} & \text{Rewrite} \ m^3 \ \text{as} \ kL \\ & \times 10^3 \ \text{to convert from} \ kL \ \text{to} \ L \end{align*} |
Hence, the pool has a capacity of \( 47 \ 600 L \).
Note: Always answer a worded question with words
3. At a friend’s party, Alex was handed a weird cup filled to the brim with cordial by the host. Not wanting to appear rude, Alex drank some of the cordial. Curious, Alex measured that the height of the cordial dropped by \( 5cm \) after he stopped drinking. How much cordial did Alex drink?
Solution:
Step 1: Calculate the volume
As we are considering the volume of the liquid that Alex drank, the cross-section will be a trapezium.
So just like in the previous example, we will have to use the formula for the area of a trapezium.
\begin{align*}
A &= \frac{3cm \times 7.5cm}{2} \times 5cm \\
&= 26.25 cm^2
\end{align*}
Then, the volume is simply
\begin{align*}
V &= A \times 6cm \\
&= 26.25cm^2 \times 6cm \\
&= 157.5 cm&3
\end{align*}
Step 2: Convert the volume into capacity
We can directly convert this into capacity using the standard conversion, \( 1cm^2 = 1ml \).
Hence, Alex drank \( 157.5 mL \) of cordial.
Note: When there are no specific units are specified by the question, the answer should be in the most appropriate units for the situation. In this case, drinks are usually measured in \( mL \). So, we answered in \( mL \).
1. Convert \( 0.00183 \ cm^3 \) to \( mm^3 \)
2. A pentagon with an area of a \( 196cm^2 \) is being used to construct a prism with a height of \( 13cm \). Determine how much space this prism occupies correct to the nearest \( cm^3 \).
3. Find the volume of the following prism, correct to the nearest \( cm^3 \)
4. A square prism toy block is being altered to make it more suitable for children to play with. Equal quarter-circle indents are made at each corner to get rid of the sharp corners. Determine the volume of the toy block correct to \(2\) decimal places.
5. Below is a regular octagonal prism such that all sides of the octagon are equal. Find the value of \(x\) and hence determine the volume of the following prism correct to \(2\) decimal places
6. Convert \(25 \ 600 m^3 \) to \(ML\)
7. Calculate the capacity of the following container in \(mL\).
8. What is the capacity of the following container as measured in litres to the nearest \(2\) decimal places
9. The local plumber, John, needs to install a \(2cm\) thick copper pipe that is \(2m\) long. The pipe has an external diameter of \(20cm\) as measured with a pair of callipers
a) Calculate the volume of copper used to manufacture the pipe to the nearest \(cm^3\).
b) What is the total amount of water that this pipe could hold to the nearest \(ml\)
10. A tall cylindrical tank is fitted with a heating element. The radius of the cylindrical tank is \(50cm\). After some heavy rainfall, a total of \(210 L \) of water was added to the tank. If the cylindrical tank was half-full before it rained, by how much did the water level rise after the rainfall to the nearest \(cm\).
1.
\begin{align*}
0.00183m^3 &= 0.00183 \times 100^3 \times 100^3 \times 10^3
&= 1 \ 830 \ 000 \ mm^3
\end{align*}
2. The question has identified that the area of the cross-section is \(196 \ cm^2 \).
Since we know the height is \( h = 13 cm \) then we can determine the volume such that:
\begin{align*}
V &= Ah \\
V &= 196 \times 13 \\
∴ V &= 2548cm^3
\end{align*}
3. The cross-section is a trapezium, hence we can use the area of the trapezium formula to determine the area of the cross-section.
\begin{align*}
A &= \frac{h}{2} (a+b) \\
A &= \frac{6}{2}(5.2 + 9.4) \\
A &= 43.8cm^2
\end{align*}
Note that the height of the prism is not in the same units of measurement as the lengths of the trapezium.
We must convert \( 205mm \) to \( 20.5cm \) in order to find the accurate volume
\begin{align*}
V &= Ah \\
&= 43.8 \times 20.5 \\
∴ V &= 897.9cm^2
\end{align*}
4. We can recognise that the cross-section is essentially a square with four quarter-circles removed.
Hence we can form the following equation for the area of the cross-section as shown below.
\begin{align*}
Let \ r \ &= \ radius \ of \ quarter \ circles \\
r &= \frac{22.4 – 18.2}{2} = 2.1 cm \\
A &= s^2 – 4 \times \frac{1}{4} \pi r^2 \\
&= s^2 – \pi r^2 \\
&= 22.4^2 – \pi (2.1)^2 \\
∴ A &= 487.905 \ cm^2
\end{align*}
Then, we identify the height is \( h = 36.8cm \), hence we can determine the volume of the toy block.
\begin{align*}
V &= Ah \\
&= 487.905 \times 36.8 \\
∴ V &= 17954.93 \ cm^3 \ (2.dp)
\end{align*}
Therefore, the volume of the toy block is \( 17954.93cm^3 \)
5.
Solution 1:
Firstly, the question asks us to determine the value of \( x \) which we can determine using simple calculations.
\begin{align*}
x = \frac{9.7 – 4}{2} = 2.85m
\end{align*}
The cross-section can be identified as a larger square with sides \( 9.7m \), with isosceles triangles cut of at each corner.
Hence, we can form an equation for the area of the cross-section as shown below.
\begin{align*}
A &= S^2 – 4 \times \frac{1}{2}bh \\
A &= 9.7^2 – 4 \times \frac{1}{2} \times 2.85 \times 2.85 \\
∴ A &= 77.845 m^2
\end{align*}
Then, we identify the height as \( h = 12.5m \), and hence we can determine the volume of the prism
\begin{align*}
V &= Ah \\
&= 77.845 \times 12.5 \\
∴ V &= 973.06 m^3
\end{align*}
Solution 2:
Using the same reasoning as above, we find that the value of \( x = 2.85m \)
The cross-section can also be identified as a rectangle and two trapeziums.
Hence, we can form an equation for the area of the cross-section as shown below.
\begin{align*}
A &= lw \times 2 \frac{h}{2}(a + b) \\
A &= (9.7 \times 4) + \big{[} 2 \times \frac{2.85}{2}(4+9.7 \big{]} \\
∴ A &= 77.845 m^2 \\
V &= Ah \\
&= 77.845 \times 12.5 \\
∴ V &= 973.06 m^3
\end{align*}
6.
\begin{align*}
25 \ 600 &= 25 \ 600 \ kL \\
&= 25.6 \ ML
\end{align*}
7. First, find the area of the cross-section of the container so that we can calculate the volume and capacity.
\begin{align*}
{A}_{rectangle} &= 5xm \times 4cm \\
&= 20 cm^2
\end{align*}
We cannot immediately calculate the area of the triangle. We must first calculate the height using Pythagoras’ theorem.
\begin{align*}
h^2 + 6^2 &= 10^2 \\
h &= \sqrt{100 – 36} \\
&= 8cm
{A}_{triangle} &= \frac{1}{2} \times 6cm \times 8cm \\
&= 24 cm^2
\end{align*}
\begin{align*}
A &= {A}_{rectangle} + {A}_{triangle} \\
&= 20cm^2 + 24cm^2 \\
&= 44cm^2 \\
V &= A \times 5cm \\
&= 220cm^3 \\
∴ V &= 220 mL
\end{align*}
8.
The cross-sectional area is a large rectangle with \(4\) congruent rectangles excluded.
\begin{align*}
A &= 16cm \times 13cm – 4(4cm \times 5cm) \\
&= 128 cm^2 \\
V &= A \times 21cm \\
&= 128cm^2 \times 21cm \\
&= 2 \ 688 \ cm^3 \\
&= 2 \ 688 \ mL \\
&= 2.69 \ L \ (2 \text{decimal places} )
\end{align*}
9. The cross-section is doughnut-shaped. As the walls of the pipe are \(2cm\) thick, then the interior circle has a radius of \(18 cm \).
\begin{align*}
{A}_{outer} &= \pi (20 \ cm)^2 \\
&= 400 \pi \ cm^2 \\
{A}_{inner} &= \pi (18 \ cm)^2 \\
&= 324 \pi cm^2 \\
A &= {A}_{outer} – {A}_{inner} \\
&= 76 \pi cm^2 \\
V &= A \times 200 \ cm \\
&= 76 \pi \ cm^2 \ \times 200 \ cm \\
&= 15 \ 200 \pi \ cm^3 \\
∴ V &= 47 \ 752 \ cm^3 \ ( \text{to the nearest} \ cm^3)
\end{align*}
The volume of copper in the pipe is \(47 \ 752 \ cm^3 \).
b) In this case, we are only concerned about the inside of the pipe. The cross-section is a circle with radius of \( 18 \ cm \).
\begin{align*}
A &= \pi (18 \ cm)^2 \\
&= 324 \pi \ cm^2 \\
V &= A \times 200 \ cm \\
&= 324 \pi \ cm^2 \times 200 \ cm \\
&= 64 \ 800 \pi \ cm^3 \\
&= 203 \ 575 \ cm^3 \ (\text{to the nearest} \ cm^3) \\
∴ V &= 203 \ 575 \ mL
\end{align*}
This pipe can hold a maximum of \( 203 \ 575 \ mL \) of water.
10. The tank being half-full does not matter, as the cross-section is uniform (i.e. the same) throughout.
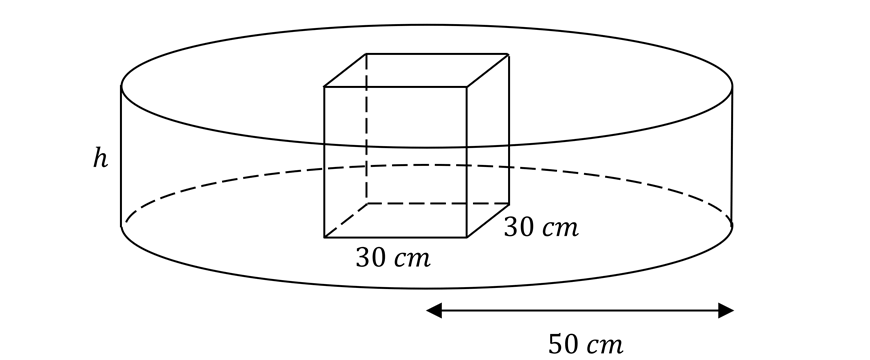
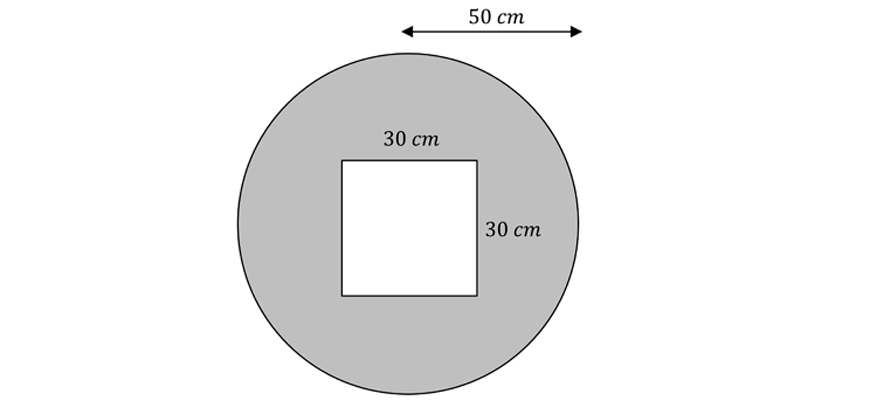
\begin{align*}
{A}_{circle} &= \pi(50 \ cm)^2 \\
&= 2 \ 500 \pi \ cm^2 \\
{A}_{square} &= 30 \ cm \times 30 \ cm \\
&= 900 cm^2 \\
A &= {A}_{circle} – {A}_{square} \\
&= 2 \ 500 \pi \ cm^2 – 900 \ cm^2 \\
&= 6 \ 954 \ cm^2 \ (\text{to the nearest} \ cm^2) \\
V &= A \ times h \ cm \\
&= 6 \ 954 \ cm^2 \times h \ cm \\
&= 6 \ 954 h \ cm^3
\end{align*}
Since the container has a capacity of \( 210 \ L \),
\begin{align*}
V &= 210 \ L \\
&= 210 \ 000 \ mL \\
&= 210 \ 000 \ cm^3
\end{align*}
Equating \( V \),
\begin{align*}
6 \ 954 h &= 210 \ 000 \\
h &= \frac{210 \ 000}{6 \ 954} cm \\
&= 30 \ cm \ (\text{to the nearest} \ cm)
\end{align*}
The water level rose by \( 30 \ cm \)
These are the most common mistakes that you need to be aware of:
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
