Welcome to Matrix Education
To ensure we are showing you the most relevant content, please select your location below.
Select a year to see courses
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Get HSC Trial exam ready in just a week
Get HSC exam ready in just a week
Select a year to see available courses
Science guides to help you get ahead
Science guides to help you get ahead

How’s your geometry? Are you confident with Year 7 Area? Don’t worry. This article will explain everything. It is very important that you have a strong grasp of Year 7 Area to set you up for other Maths topics in the future.
| Stage 4 NESA Syllabus | |
| Syllabus | Explanation |
| Choose appropriate units of measurement for area and convert from one unit to another (ACMMG195) | This means that you know how to convert \( 100cm^{2} \ to \ m^{2} \) |
| Establish the formulas for areas of rectangles, triangles and parallelograms and use these in problem-solving (ACMMG159) | This means that you know, understand and can use standardised formulas to find areas of different shapes. |
In this section, students are exposed to questions involving the usage of area.
We will be:
Area is the amount of 2-dimensional space a surface covers. As area is 2D, it has no thickness or depth.
Measurements in area are distinct as unlike length which uses \(cm, m, km\) and many more. Area uses \(cm^{2}, m^{2}, km{2} \) instead.
Note: these are commonly said as square centimetres, square metres and square kilometres but saying centimetres squared, metres squared and kilometres squared would be just as accepted.
Improve your area skills with these must-do questions! Fill out your details below to get this resource emailed to you. "*" indicates required fields
Master Area with this Maths Worksheet!

Master Area with this Maths Worksheet!
The bulk of calculating area is just multiplication. However, knowledge of basic arithmetic like addition and subtraction may also be helpful in harder questions.
Area will also require the knowledge of certain features of particular geometrical shapes.
For example, if given that a shape is a square, we need only know the length of 1 side to calculate its area.
This is in comparison to a rectangle, where we need to know both its length and breadth before calculating area.
Similar to length, there are many units used for area.
These all have their usages depending on the size of the surface in question.
For example, a coin may be measured in millimetres squared while a large farm property would be measured in hectares.
Remember: \(1\) hectare is a square of sides \(100m\) giving an area of \(10 000m^{2}\) per hectare.
When performing conversions, it is extremely important to remember that the little \(2\), above the unit signifies that it is squared.
Therefore, when converting, we must multiply or divide by the normal amount squared.
Below is a conversion flowchart, which simplifies and visually makes clear the conversion rates across the different square units.
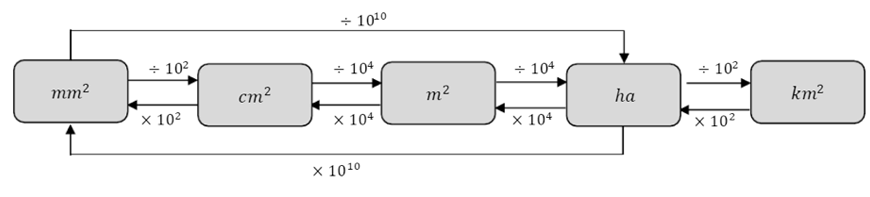
Example
1. Convert \( 1000m \) into \( km^{2} \)
Solution:
To go from \( m^{2} \) to \( km^{2}\), we follow the arrows and divide by \(1000^{2}\)or \(1 000 000\).
This gives us \(0.001km^{2}\).
We can convert this without looking at the conversion chart. Think of it as normally converting from metres to kilometres… we divide by \(1000\).
So, because we are working with area, this is squared units.
This means that we must divide by \(1000\) instead.
Calculating the area of squares and rectangles are quite simple. All that must be done is to multiply the two adjacent sides together.
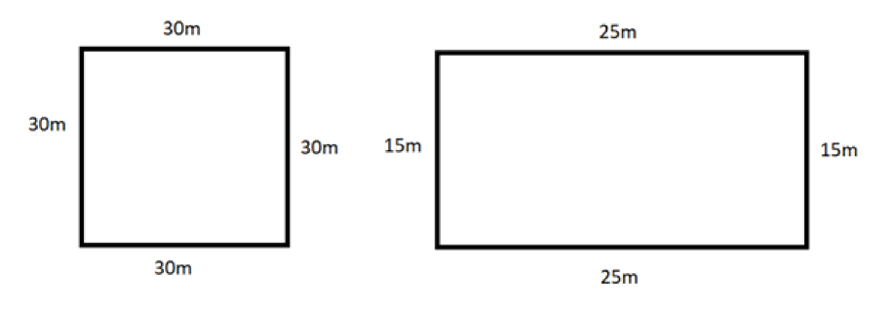
Given that the figure on the left is a square while the figure on the right is a rectangle.
For the square, \(A \ = \ 30 \times 30 = 900m^{2} \)
For the rectangle, \(A \ = \ 15 \times 25 = 375m^{2} \)
Note: All sides of a square are equal. So, when given one side length of the square, we can simply square \( (x^{2}) \) that value to receive the square’s area.
For a rectangle, however, we must know its length and breadth. Multiplying these two will give us the area.
Standardised formulas:
\begin{align*}
AREA \ OF \ SQUARE \ = s^{2}
\end{align*}
Where \(s\) is the length of the sides.
\begin{align*}
AREA \ OF \ RECTANGLE \ = l \times b
\end{align*}
Where \(l\) is the length and \(b\) is the breadth.
To calculate the area of a triangle, we must multiply the perpendicular height to the base and then divide by \(2\).
Now, consider the triangles below.
For the first triangle, the \(base\) and \(height\) are the two sides with the right angle in between them.
If we were to reflect another of the same triangle along the hypotenuse (the side opposite the right angle), we would be met with a rectangle.
Therefore, it can be seen that by halving the area of a rectangle, we are left with a right-angled triangle.
Looking at the second triangle, we can see that it was simply split into two right-angled triangles.
If we reflect along the two hypotenuses of the newly made right-angled triangles, we can see we are once again met with a rectangle.
This proves that the formula works for these types of triangles as well.
Lastly, on the third triangle, the small right-angled triangle bounded by the dotted lines is subtracted from the larger right-angled triangle.
We can prove that the desired area will simply be \( \frac{1}{2} \) the perpendicular height multiplied by the base as well. But a lot of algebra will be required.
For the purpose of Year 7, it is just important to identify what the perpendicular height and base of any triangle would be.
However, if you would like a challenge, try proving the third triangle will also satisfy the formula, \( Area = \frac{1}{2} \ base \times height \).
Standardised formula:
\begin{align*}
AREA \ OF \ TRIANGLE \ = \frac{1}{2} bh
\end{align*}
Example:
1. Find the area of this triangle
Solution:
Looking at this triangle, we can see that the base is \(15cm\) while the perpendicular height is \(132mm\).
We will first convert to a common unit, let’s pick \(mm\).
Therefore, the base is \(150mm\) and the perpendicular height is \(132mm\).
The area is therefore \(\frac{1}{2} \times 132 \times 150\), which is equal to \(9900mm^2\).
To answer the question in terms of \(cm^2\), we would have converted the height to \(13.2cm\).
Multiplying \(13.2\) to \(15\) and then dividing by \(2\) gives us \(99cm^2\).
Using our knowledge of conversion covered earlier, we can see that these two answers are exactly the same.
For simple non-standard quadrilaterals, it is best to first divide the shape into two triangles, if possible.
From here, we treat the shape as two independent triangles and calculate the area independently for each.
After that, we simply add the two areas together to get the total area.
Example
1. Find the area of quadrilateral ABCD given AC = 10mm
Solution:
We can see that quadrilateral \(ABCD\) can be split into two triangles, \(ABC\) and \(ACD\). Triangle \(ABC\) has perpendicular height \(3\), base \(10\), while \(ACD\) has perpendicular height \(5\), base \(10\).
\begin{align*}
Area_{total} &= A_{ABC} + A_{ACD} \\
Area_{total} &= (\frac{1}{2} \times 3 \times 10) + (\frac{1}{2} \times 5 \times 10) \\
Area_{total} &= 15 + 25 \\
Area_{total} &= 40 mm^{2}
\end{align*}
A parallelogram is a quadrilateral whose opposite sides are parallel and of equal length.
When calculating the area of a parallelogram, we simply multiply base by height.
Consider the standard parallelogram below.
Opposite sides of a parallelogram are equal.
So, when we remove the inner rectangle… the outer triangles are of equal size.
This means that we can essentially create two rectangles out of a parallelogram.
Hence, we can see how the formula for a parallelogram works.
Standardised formula:
\begin{align*}
AREA \ OF \ A \ PARALLELOGRAM \ = bh
\end{align*}
Where \( b \) is the base and \(h\) is perpendicular height.
Example:
1. Find the area of the given parallelogram.
Solution:
The area of a parallelogram is always the base multiplied by the height.
Looking at this diagram, we can quite easily see that the perpendicular height is \(8.6m\).
However, what do we choose for the base?
The answer to that is the \(14.3m\).
We know this because it is perpendicular to the perpendicular height while the \(10.3m\) side is parallel.
Therefore,
\begin{align*}
A \ = \ 14.3 \times 8.6 \\
A \ = \ 122.98m^{2}
\end{align*}
A rhombus is a quadrilateral which has all sides equal, opposite sides parallel and also, its diagonals bisect at right angles.
Looking at the rhombus with diagonals marked in, we can see \(4\) identical right-angled triangles.
Therefore, the total area must be:
\begin{align*}
Area_{total} &= 4 \times \frac{1}{2} \times p \times q \\
Area_{total} &= 2pw
\end{align*}
However, \(p\) and \(q\) are both half lengths of their respective diagonals.
Hence, calling diagonal \(2p\) as \(x\), and \(2q\) as \(y\).
We get that
\begin{align*}
Area_{total} &= 2 \times \frac{x}{2} \times \frac{y}{2} \\
Area_{total} &= \frac{xy}{2}
\end{align*}
Standardised formula:
\begin{align*}
AREA \ OF \ A \ RHOMBUS \ = \frac{xy}{2}
\end{align*}
Where \( x \) and \(y\) are the two diagonals.
Example
1. Find the area of the given rhombus
Solution:
We know that the area of a rhombus is the diagonals multiplied together divided by \(2\).
We also know that a property of rhombuses is that their diagonals bisect each other.
Thus, the diagonals must be \(2×4\) and \(2×7\).
Which is \(8\) and \(14\).
Therefore,
\begin{align*}
A \ = \ 8 \times 14 \times \frac{1}{2}\\
A \ = 56cm^{2}
\end{align*}
A trapezium is a quadrilateral with one set of opposite parallel sides.
To calculate its area, we will once again, divide it into simple shapes such as triangles and rectangles.
\begin{align*}
Area_{total} &= Area_{left-triangle} + Area_{rectangle} + Area_{right-triangle} \\
Area_{total} &= \frac{1}{2}xh + ah + \frac{1}{2}hy \\
Area_{total} &= \frac{xh}{2} + \frac{2ah}{2} + \frac{hy}{2} \\
Area_{total} &= \frac{xh + 2ah + hy}{2} \\
Area_{total} &= h\frac{x + 2a + y}{2} \\
Area_{total} &= h \big{(} \frac{a+b}{2} \big{)} \\
Area_{total} &= h \big{(} \frac{a+b}{2} \big{)} (Note \ that \ x + a + y = b)
\end{align*}
Here we are left with the formula of a trapezium.
Standardised formula:
\begin{align*}
AREA \ OF \ A \ TRAPEZIUM = h\frac{a+b}{2}
\end{align*}
Where \(a\) and \(b\) are the lengths of the parallel sides and \(h\) is the perpendicular height.
Example
1. Find the area of this trapezium
Solution:
Looking at this trapezium, we can see the length of the parallel sides are \(10\) and \(14\), while the perpendicular height is \(10\).
Therefore,
\begin{align*}
A &= 10 \big{(} \frac{10 + 14}{2} \big{)} \\
A &= 10 \big{(} \frac{24}{2} \big{)} \\
A &= 10(12) \\
A &= 120cm^{2}
\end{align*}
Composite figures are figures made up of two or more shapes.
To find the area of more complex composite figures, we will employ the same tactic we used to define the area for the more complex quadrilaterals.
That is, we will divide into more simple shapes and then add it all up.
Example
1. Find the area of the shape below.
Solution:
This shape can be split into a rectangle and what seems to be a parallelogram.
The dimensions of the rectangle are already given. But to find the dimensions of the parallelogram, we must first recall that the opposite sides of a rectangle are equal.
This gives us that the bottom end of the rectangle is \(20.9m\) as well.
As there is also a dash in the bottom side of the parallelogram.
We know that this shape MUST be a parallelogram, as there is one set of equal and parallel sides.
After that, we can minus \(22.7\) by \(14.3\) to find the perpendicular height.
Upon annotating your diagram, it becomes much easier to see how we can arrive at our final answer.
\begin{align*}
Area_{total} &= A_{rectangle} + A_parallelogram \\
Area_{total} &= (20.9 \times 14.3) + (20.9 \times 8.4) \\
Area_{total} &= 298.87 + 175.56 \\
Area_{total} &= 474.43m^{2}
\end{align*}
Note: it may be easier to simply calculate a larger shape than what is given first, then subtracting off the excess. This is demonstrated by the example below.
2. Find the area of the shape below.
Solution:
The more direct way to approach this question would be to split it into three separate rectangles and then add them all up.
However, this shape seems to just be a large rectangle with a small rectangular chunk taken out of it.
Therefore, we can approach this question in a different manner.
\begin{align*}
Area_{total} = Area_{large-rectangle} – A_{small-rectangle}
\end{align*}
The dimensions of the large rectangle will be \(10.7cm\) for its length, and \(2.3 + 4.6 + 2.3\) for its breadth, \(9.2cm\).
We know this because \(2.3\) is demonstrated by a singular dash.
The dimensions of the smaller rectangle will be \(4.6cm\) for its length and \(3.6cm\) for its breadth.
\begin{align*}
Area_{total} &= (10.7 \times 9.2) – (4.6 \times 3.6) \\
Area_{total} &= 98.44 – 16.56 \\
Area_{total} &= 81.88cm^{2}
\end{align*}
Worded questions involving area requires an in-depth understanding of the different concepts we learn in Area.
With most information now in word form, we are required to think a bit more about what we need to find.
Example
1. 1250 metres of fencing was used to enclose a rectangular paddock. The paddock is \(375\) metres long. Find the paddock’s area.
Solution:
Starting off, we know that the paddock is a rectangle.
That means that it has two sets of equal sides.
Therefore, if the length is \(375m\) and the perimeter is \(1250m\), we can minus \(2×375 (750)\) from \(1250\) to get the combined length of the two breadths.
This gives us \(500\), and as the breadths are equal, we know that one will just be \(250m\).
Thus, the area, being breadth multiplied by length will just be \(250 \times 375 \times 93750m^{2}\).
For worded questions, sometimes drawing a diagram may assist in your understanding.
We strongly recommend doing so if you cannot see a clear set of steps to find your answer.
It is important to remember all the standardised formulas, covered in this guide.
\begin{align*}
AREA \ OF \ SQUARE &= s^{2} \\
AREA \ OF \ RECTANGLE &= l \times b \\
AREA \ OF \ TRIANGLE &= \frac{1}{2}bh \\
AREA \ OF \ A \ PARALLELOGRAM &= bh \\
AREA \ OF \ A \ RHOMBUS &= \frac{xy}{2} \\
AREA \ OF \ A \ TRAPEZIUM &= h \frac{a + b}{2}
\end{align*}
It may help in remembering these by understanding how each formula was derived.
Additionally, remembering the certain characteristics of different quadrilaterals will assist particularly in finding the area of composite figures.
Occasionally, you will have to use properties of the quadrilateral to answer the question.
Something else to not forget is conversion rates between different units of area.
The prefixes are the same as usual… but remember as area is squared, we must square the normal prefix difference as we convert.
One last tip for composite figures (which are normally the hardest questions involving area ).
Remember to annotate the diagram with what you already know.
This will assist in helping you see the correct path needed to reach your answer.
© Matrix Education and www.matrix.edu.au, 2025. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.