Welcome to Matrix Education
To ensure we are showing you the most relevant content, please select your location below.
Select a year to see courses
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Get HSC Trial exam ready in just a week
Get HSC exam ready in just a week
Select a year to see available courses
Science guides to help you get ahead
Science guides to help you get ahead

Angle relationships is an essential topic because it forms the foundation of many different Maths topics that you will come across in the future. In this guide, we will give you the best tips to work with angle relationships.
We will be looking at NSW Syllabus Outcomes:
| NSW Stage 4 Syllabus Outline | |
| Syllabus | Explanation |
| Demonstrate that the angle sum of a triangle is 180o and use this to find the angle sum of a quadrilateral (ACMMG166) | This means that you will know how to identify and figure out angle sizes in supplementary angles. |
| Establish properties of quadrilaterals using congruent triangles and angle properties, and solve related numerical problems using reasoning (ACMMG202) | This means that you know how to use different angles on a point and angles associated with parallel lines. |
| Identify, name and measure alternate angle pairs, corresponding angle pairs and co-interior angle pairs for two lines cut by a transversal (ACMMG163) | This means that you can work out sizes on different angles by looking at alternate, corresponding and co-interior angle pairs. |
| Solve simple numerical problems using reasoning (ACMMG164) | This means that you are able to questions like: “Find the value of \( \alpha° \) in the diagram” |
Understanding and learning angle relationships may be easy… But the majority of students face difficulty when applying angle relationships.
They also struggle with presenting answers in a coherent way that’s not obtuse. This means that markers will struggle to follow the reasoning provided.
These are the main difficulties faced by students in this topic:
This guide will help you overcome these difficulties, as well as covering the following content:
To do well in Angle Relationships, you need to know about:
Students should be familiar with how to name lines as well as angles.
Lines should be named as a group pair of letters.
For example, the diagram below shows the lines \( AB \).
To name angles, identify the vertex and the two letters at the end of each ray.
In the case below,
To name the angle above, the middle letter should represent its vertex.
Thus the angle can be named as such:
\begin{align*}
\angle ABC \ or \ \angle CBA \ or \ \angle B
\end{align*}
Two angles that add up to \( 90º\) are called complementary angles.
Similarly, two angles that add up to \( 180º\) are called supplementary angles.
Angles at a point form a revolution add up to \( 360° \).
In the diagram below:
Example
1. Find the size of \( x \).
Solution
To determine the size of \( x \), we need to utilise the fact that angles at a point add to \( 360°\).
As a result,
\begin{align*}
x°+ 2x° + (x-30)° + 90° &= 360° \ (\text{Angles of a revolution add to} \ 360°) \\
4x° – 30° + 90° &= 360° \\
4x° &= 300° \\
∴ x° &= 75º
\end{align*}
When two straight lines intersect, the two pairs of opposite angles formed are equal.
These are known as vertically opposite angles.
In the diagram below:
Parallel lines are lines in a plane that do not intersect or touch each other at any point.
Notation: Parallel lines are marked with arrowheads pointing in the same direction.
In the diagram:
To represent that \( AB \) and \( CD \) are parallel, we use the parallel symbol and notate as \( AB \parallel CD \)
A transversal is a line that crosses two or more lines.
In the diagram, the transversal \( EF \) cuts the lines \( AB \) and \( CD \).
Transversals which cross parallel lines, give rise to three fundamental parallel angle relationships (Alternate, Corresponding and Co-interior angles).
Alternate angles are angles on opposite sides of the transversal and between the parallel lines.
Alternate angles on parallel lines are equal.
In the diagram below,
An example of written reasoning could be,
\(\angle AXY = \angle XYD \ (\text{Alternate angles on parallel lines} \ AB \ \text{and} \ CD \ \text{are equal}) \)
Corresponding angles are angles on same sides of the transversal. One angle is between the parallel lines while the other is outside. Corresponding angles on parallel lines are equal.
In the diagram below:
An example of written reasoning could be,
\( \angle AXY = \angle CYF \ (\text{Corresponding angles on parallel lines} \ AB \ \text{and} \ CD \ \text{are equal}) \)
Co-interior angles are angles on same sides of the transversal between the parallel lines.
Co-interior angles are supplementary (add up to \(180°\))
In the diagram below:
An example of written reasoning could be:
Co-interior angles can be identified by a “C” orientation as shown in the bold lines in the diagram below.
Example
1. Find the value of \( \beta \)
Solution
\begin{align*}
\angle EXB &= \angle AXY = 30° \ (\text{Vertically opposite angles are equal}) \\
\beta° &= 180° – \angle AXY \ (\text{Co-interior angles on parallel lines are supplementary})\\
\beta° &= 180° – 30° \\
\beta° &= 150°
\end{align*}
Conversely, we can use these angle relationships to prove that two lines are parallel.
This occurs when one or more of the following relationships hold:
Example
1. Prove that \( AF \) and \( CE \) are parallel
Solution
\begin{align*}
<AXB &= \angle GXF = 79° \ \ (\text{Vertically opposite angles are equal}) \\
<YXF &= 180° – <HXG \ – \angle GXF \ \ (\text{Angle sum of straight lines}) \\
<YXF &= 180° – 70° – 79° \\
<YXF &= 31° \\
<YXF &= \angle DYE = 31°\\
∴ AF \ &and \ CE \ are \ parallel \ \ (\text{Corresponding angles} \ \angle YXF \ \text{and} \ \angle DYE \ \text{are equal})
\end{align*}
The following is a summary of the angle relationships covered in the post:
| Angle relationship | Description | Diagram | Explanation |
| Complementary angles | Angles add to \( 90° \) | 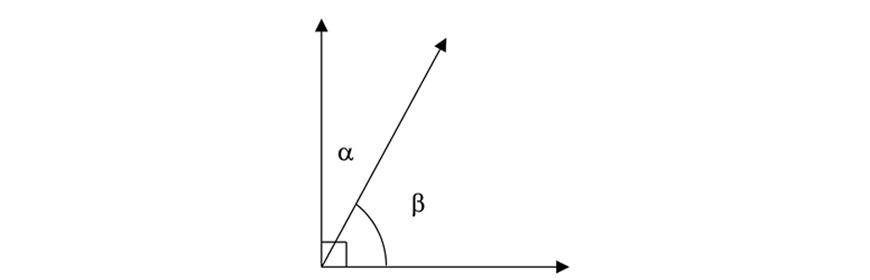 | \( \alpha + \beta = 90° \) |
| Supplementary angles | Angles add to \( 180° \) | 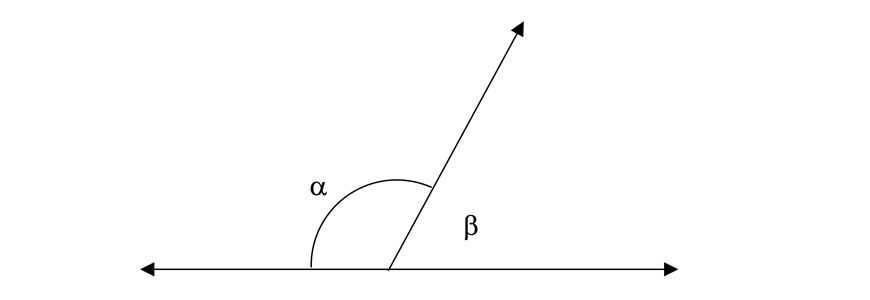 | \( \alpha + \beta = 180° \) |
| Angles at a point | Angles add to \( 360° \) | 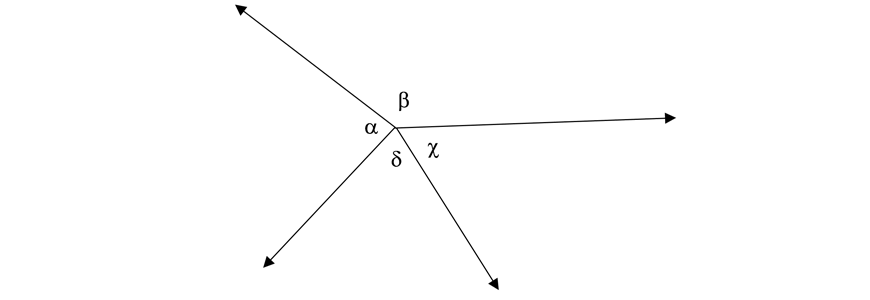 | \( \alpha + \beta + \gamma + \delta = 360° \) |
| Vertically opposite angles | Angles are equal | 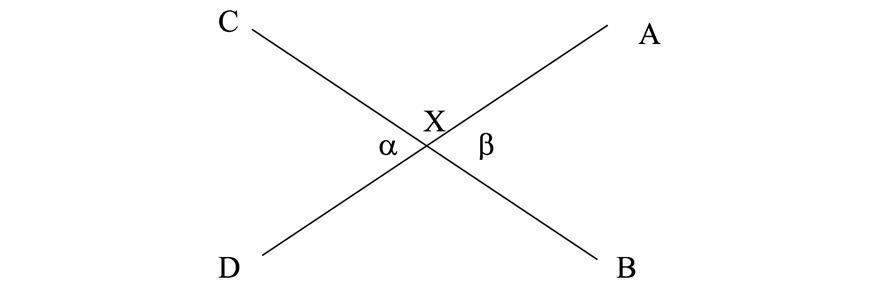 | \( \alpha = \beta\) |
| Alternate angles | Angles are equal | 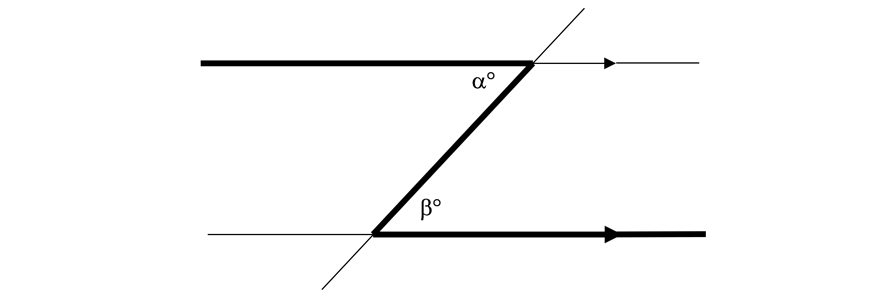 | \( \alpha = \beta\) |
| Corresponding angles | Angles are equal | 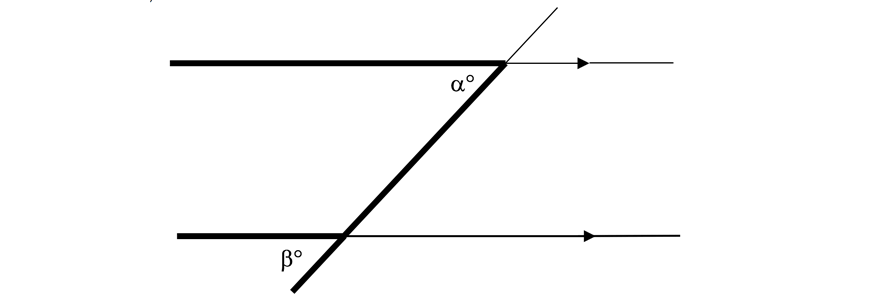 | \( \alpha = \beta\) |
| Co-interior angles | Angles are supplementary | 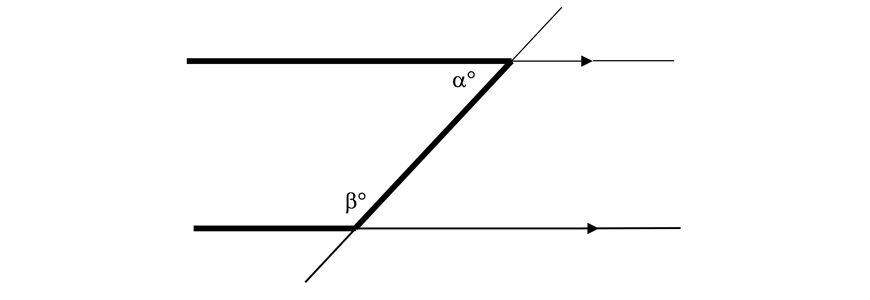 | \( \alpha + \beta = 180° \) |
1. Given that \( \alpha° \) and \( \beta° \) are complementary, what is value of \( \beta° \) if \( \alpha° = 54° \)
2. Find the value of \( \alpha° \) and \( \beta° \) in the following diagram
3. Prove that \( BC \) and \( DE \) are parallel.
4. Find the size of \( \alpha° \)
5. Find the size of \( \alpha° \)
1.
\begin{align*}
\beta° = 36°
\end{align*}
2.
\begin{align*}
\beta° &= 180° – \angle AXB \ (\text{Angle sum of straight line}) \\
\beta° &= 94° \\
\angle EXC &= \angle AXB = 86° \ (\text{Vertically opposite angles are equal}) \\
\alpha° + 26° &= 86° \\
\alpha° &= 60°
\end{align*}
3.
\begin{align*}
\angle{CBD} &= \angle{BAC} + \angle{ACB} \ (\text{Exterior angle sum of triangle}) \\
\angle{CBD} &= 126° \\
\angle{CBD} &+ \angle{BDE} \\
&= 126° + 54° \\
&= 180° \\
\end{align*}
\begin{align*}
∴ BC \ \text{and} \ DE \ \text{are parallel Co-interior angles , angles} \angle{CBD} \ \text{and} \ \angle{BDE} \text{are supplementary on parallel lines})
\end{align*}
4.
\begin{align*}
\angle CDA &= \angle DEB = 125° \ (\text{Corresponding angles on parallel lines} \ AK \ \text{and} \ BL \ \text{are equal}) \\
\angle DEB &= \angle HIE = 125° \ (\text{Corresponding angles on parallel lines} \ CF \ \text{and} \ GJ \ \text{are equal}) \\
\alpha° & = \angle HIE = 125° \ (\text{Vertically opposite angles are equal})
\end{align*}
5. Construct \( EF \) so that it is parallel to \( AB \) and \( CD \)
\begin{align*}
\angle BEF &= 180° – 35° \ (\text{Co-interior angles on parallel lines} \ AB \ \text{and} \ EF \ \text{are supplementary}) \\
\angle BEF &= 145° \\
\angle CEF&= 180° – 46° \ (\text{Co-interior angles on parallel lines} \ CD \ \text{and} \ EF \ \text{are supplementary}) \\
\angle CEF &= 134° \\
∴\alpha° &= \angle BEF + \angle CEF \\
\alpha° &= 279°
\end{align*}
© Matrix Education and www.matrix.edu.au, 2025. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.