Part 3: How to Study for UCAT Quantitative Reasoning

UCAT Quantitative Reasoning

What is Quantitative Reasoning in UCAT?

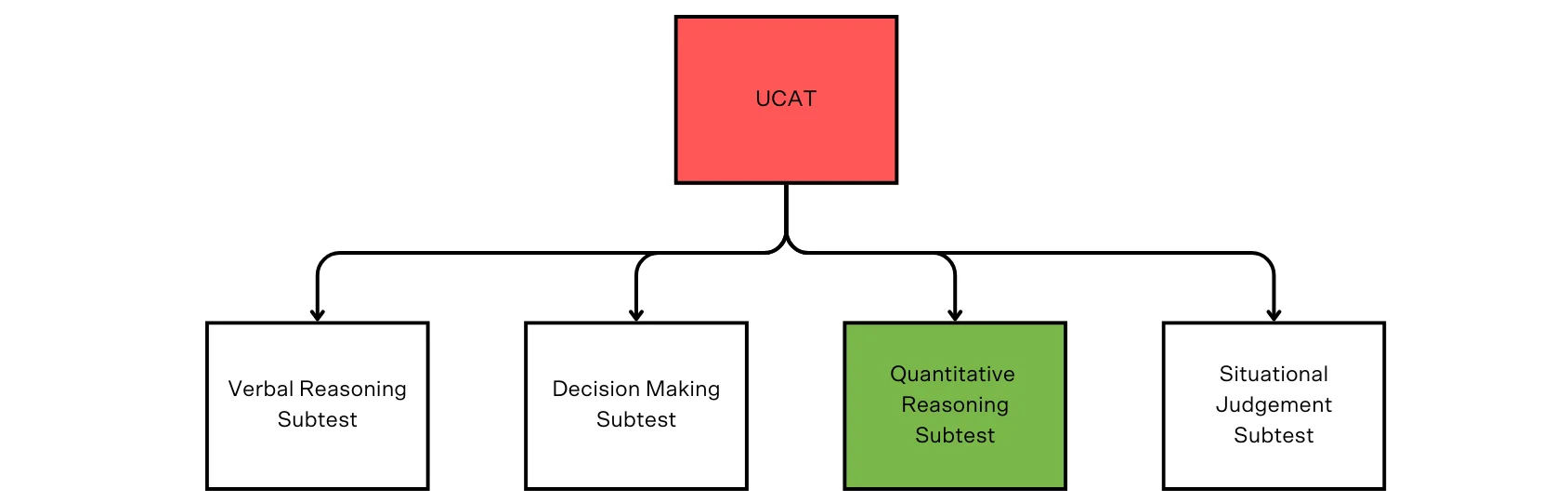
The UCAT Quantitative Reasoning section is the third of the five subtests. It assesses your numerical abilities to solve problems quickly. This section will demand some math skills but will have more to do with problem-solving.

Why is Quantitative Reasoning tested?

Doctors, dentists, and/or medical professionals often need to make quick decisions based on mathematical calculations. These decisions demand effective and efficient problem-solving skills to manage risks and assess situations.

Don’t leave UCAT to chance

Our UCAT Experts can help you ace UCAT. We’ll help you get exam-ready with our step-by-step approach to building your logical thinking abilities, critical thinking skills and moral and ethical standards. Learn more about Matrix UCAT Course.

The Quantitative Reasoning subtest

What is the format of the Quantitative Reasoning subtest?

The Quantitative Reasoning subtest consists of 36 questions that must be completed in 24 minutes – that results in an average of 40 seconds per question.

With limited time, you’ll need to make decisions efficiently and effectively.

Questions may involve charts, graphs and reference tables which may demand more time to solve.

What are the calculation types of Quantitative Reasoning questions?

The flowchart below illustrates the different categories in the Quantitative Reasoning subtest:

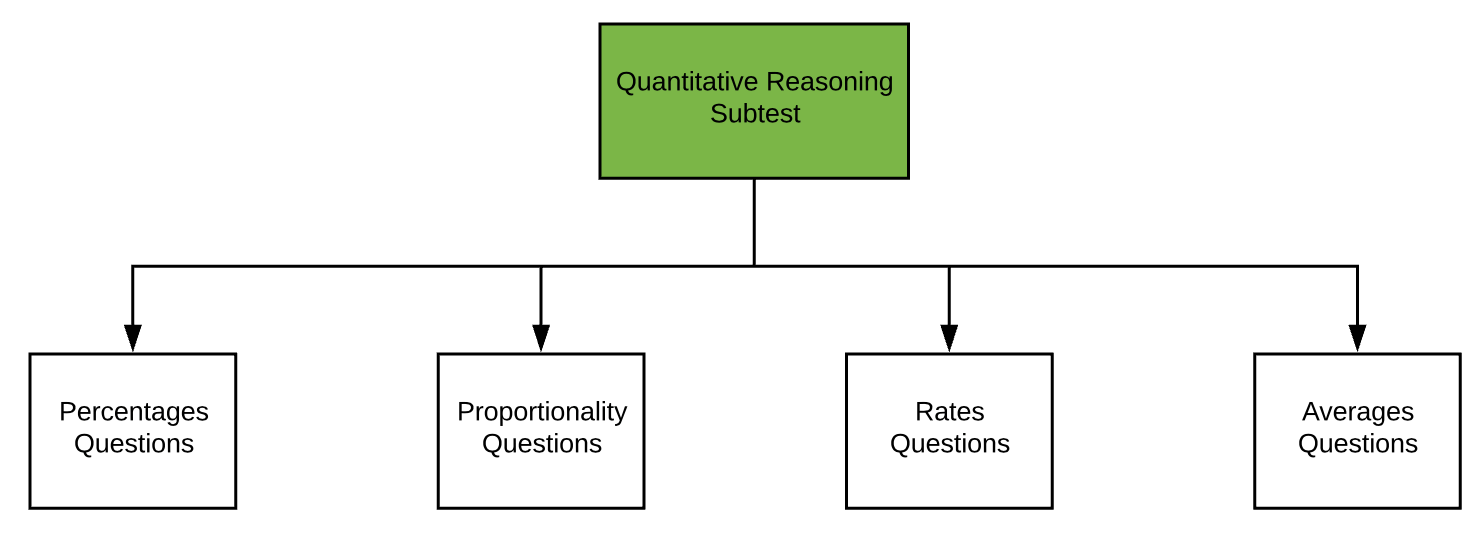
In Quantitative Reasoning, calculation questions can vie categorised into four different types:

• Percentages: Calculating the increase/decrease of percentage changes in cost prices or quantities. Some questions may ask you to convert percentages into decimals or fractions.
• Proportionality: Calculating the direct and indirect proportion, e.g: the proportional increase or decrease of a value
• Rates: Calculating the rate or speed of flow.
• Averages: Calculating the mean, mode or median for values that may be presented in the form of charts, tables or diagrams.

Examples of Quantitative Reasoning questions

Here’s an example of a Quantitative Reasoning question:

Sarah’s school is trying to raise funds to build a new hall for the students. Her class decides to hold a bake sale to contribute to some of the funds. She is making a batch of muffins for her school bake sale. She has the following recipe below:

Choc chip muffin recipe:

• 125mL oil
• 100g sugar
• 100g choc chips
• 250g flour

Question 1 (Proportionality)

This recipe produces 1 tray; however, Sarah is baking 5 trays. How much will the ingredients cost?

A) $5.50

B) $5.80

C) $6.20

D) $6.50

E) $7.10

Answer

E

A common mistake is using incorrect quantities of the ingredients. Remember that you can only buy ingredients in specified quantities at the supermarket!  For example, 625mL of oil is required, and as a result, 750mL of oil must be bought.  Hence, the ingredients cost $1.80 for flour (3×0.60), the oil costs $3.60 (3×1.20), the sugar $1 and the choc chips $0.70, which added together is $7.10.

Question 2 (Percentages)

Sarah ends up eating one tray during the baking process so ends up spending $7.50 altogether to make 5 trays and one that has already been consumed. Each sellable tray has 10 muffins, and each muffin sold for $1.50. What percentage of her earnings are profit? (Assuming all muffins are sold)

A) 10%

B) 50%

C) 90%

D) 95%

E) Can’t tell

Answer

C

Each of the 5 trays has 10 muffins, which means 50 sellable muffins in total. If each is sold for $1.50 then Sarah makes $75 (50x$1.50).

However, of the total income, $7.50 was spent on ingredients, which is 10% of $75. Therefore 90% is profit (100-10).

Question 3 (Ratios)

At the end of the day when the bake sale finishes Sarah still has a lot of muffins left, therefore she decides to discount the price of each muffin from $1.50 to $1.00 so she doesn’t have to repack them and take them home. Having sold everything, Sarah makes $65 gross profit. What ratio of full price squares to discounted squares did Sarah sell?

A) 1:2

B) 1:1

C) 3:2

D) 2:3

E) Can’t tell

Answer

C

This can be solved by using simultaneous equations: if x is the number of full price muffins and y discounted muffins then x + y=50. At the same time the earnings add up to $65, and x is sold at $1.50 and y at $1, therefore 1.5x + y=65. Substituting one equation into the other results in x=30 and y=20, so the ratio is 3:2.

Don’t leave UCAT to chance