Select a year to see courses
Select a year to see available courses
Are you ready for your Year 11 Physics Yearly Exam? Test yourself with these commonly asked exam questions.
Join 75,893 students who already have a head start.
"*" indicates required fields
The Matrix Year 11 Physics Yearly Exam Paper contains questions based on the new Year 11 Physics syllabus and covers the four modules of Year 11 Physics course:
We have listed below 12 must know questions for your quick reference.
Test your knowledge and understanding with our 2-hour Year 11 Physics Yearly Exam Practice Paper.
Commonly asked exam questions on Module 1 Kinematics are:
A ball is released from a height of \(1.5 \ \text m\).
What is the magnitude of the ball’s velocity when the ball is \(0.5 \ \text m\) above the ground? Ignore the effects of air resistance. Ignore the effects of air resistance.
(A) \(3.1 \ \text {ms} ^{-1}\)
(B) \(4.4 \ \text {ms} ^{-1}\)
(C) \(9.8 \ \text {ms} ^{-1}\)
(D) \(9.6 \ \text {ms} ^{-1}\)
A police car is chasing a motorbike as shown in the diagram below.
Data
(a) Sketch a labelled vector diagram, showing how the velocity of the motorbike relative the police car \(v ⃗_MP\) can be determined. (2 marks)
(b) Determine the velocity of the motorbike relative to the police car. (2 marks)
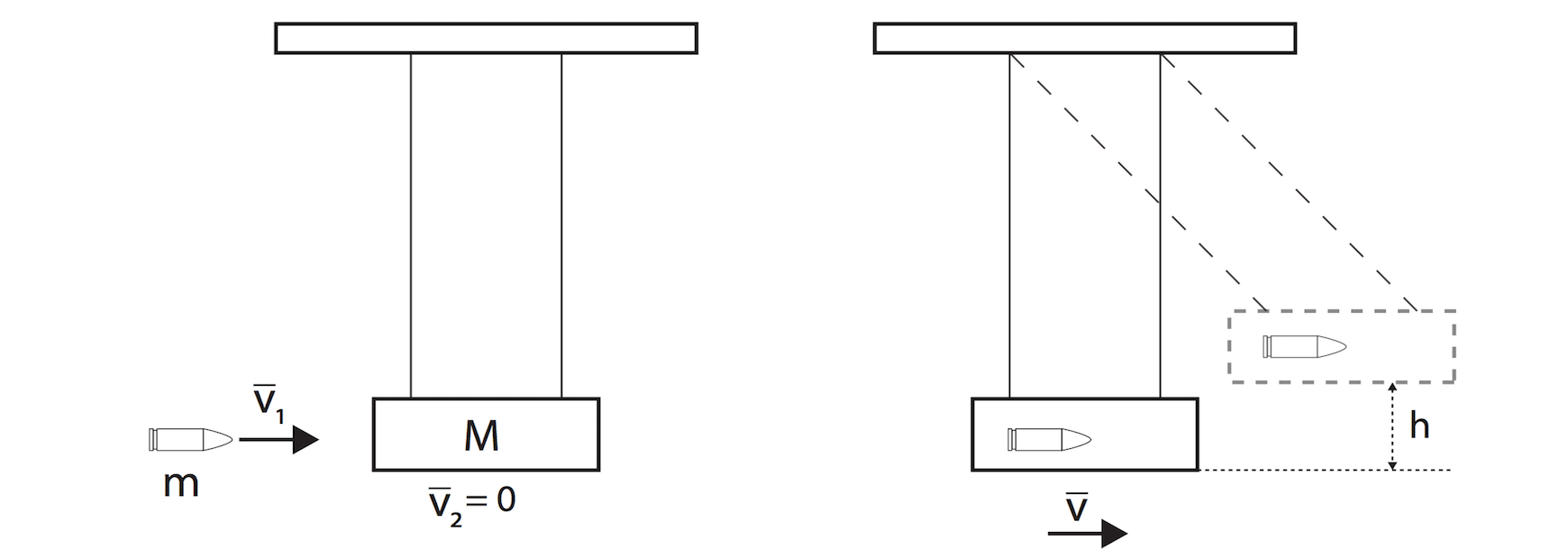
Commonly asked exam questions on Module 2 dynamics are:
Madison pushes a box across her bedroom floor by applying a force of \(100 \ \text N\) as shown.
Which of the following statements is true regarding the forces acting on the box? The box moves at a constant speed.
(A) \(\text N = \text W\)
(B) \(\text N > \text W\)
(C) \(\text f = 100 \ \text N\)
(D) \(\text f = (100 \ \text {sin} \ 20°) \text N\)
To determine the static and kinetic coefficients of friction between a block and a surface, students set up the experiment shown below.
Pulling a block of known weight at constant speed using a spring balance allows the coefficients of friction to be determined. Which of the following graphs represents how the force applied varies with time?
A cricket ball of mass \(150 \ \text g\) is hit by a bat of mass \(1.4 \ \text {kg}\). The force acting on the ball against time is shown in the graph below.
What is the change in momentum of the cricket ball and the cricket bat?
| Change in momentum of cricket ball | Change in momentum of cricket bat | |
| (A) | \(1.5 \ \text {kg m/s}\) | \(0\) |
| (B) | \(1.5 \ \text {kg m/s}\) | \(–1.5 \ \text {kg m/s}\) |
| (C) | \(3 \ \text {kg m/s} \) | \(–3 \ \text {kg m/s}\) |
| (D) | \(3 \ \text {kg m/s}\) | \(0 \ \text {kg m/s}\) |
A \(2.0 \ \text {kg}\) mass is placed on a slope and connected to an unknown mass \( \text M\) by an inextensible string over a pulley. The \(2 \ \text{kg}\) mass accelerates down the slope at \(1.0 \ \text{ms}^{-2}\) and the unknown mass \( \text M\) slides up along the top surface of the \(2 \ \text{kg}\) mass as shown in the diagram below.
Ignore the effects of friction and the mass of the pulley is negligible.
Calculate:
(a) The magnitude of the net force on the \(2.0 \ \text {kg}\) mass. (1 mark)
(b) The magnitude of the tension in the string. (2 marks)
(c) The unknown mass \( \text M\). (2 marks)
Be one step ahead of your peers with advanced completion of contents before it’s taught at school. You’ll gain an in-depth knowledge and understanding of the key concepts for exam success.
Popular exam questions on Module 3 Waves and Thermodynamics are:
Below is an oscilloscope trace of two waves that interfered to produce a beat pattern.
If the period labelled \(1/f_ {\text {beat}}\) is \(0.1 \ \text s\), what are the two frequencies that created the waveform?
(A) \(10 \text {Hz}\) and \(20 \text {Hz}\)
(B) \(95 \text {Hz} \)and \(105 \text {Hz}\)
(C) \(100 \text {Hz}\) and \(110 \text {Hz}\)
(D) \(105 \text {Hz}\) and \(115 \text {Hz}\)
The diagram below shows an organ pipe of length L that is closed at one end and open at the other end. Ignore any end effects.
The velocity of sound in air is \(v_{0}\). What are the frequencies of the first harmonic and the first overtone respectively?
| First Harmonic | First overtone | |
| (A) | \(\frac{v_0}{4 \text L}\) | \(\frac{v_0}{4 \text L}\) |
| (B) | \(\frac{(3v_0)}{4 \text L}\) | \(\frac{v_0}{\text L}\) |
| (C) | \(\frac{v_0}{4 \text L}\) | \(\frac{(3v_0)}{4 \text L}\) |
| (D) | \(\frac{v_0}{2 \text L}\) | \(\frac{v_0}{\text L}\) |
An experimental setup for determining the velocity of sound in air is shown below.
A \(680 \ \text{Hz}\) tuning fork is set into vibration and held just above the open end of a tube partially submerged in water. The length of the air column in the tube is increased until a resonance is heard. The length of the air column in the tube is then increased by changing the positions of water level until the next resonance is heard.
(a) Explain why the sound heard from the first resonating length is louder than the tuning fork. (2 marks)
(b) Calculate the wavelength of the sound waves in the air column. (2 marks)
(c) Hence or otherwise, calculate the speed of the sound wave in the air column. (1 mark)
Popular exam questions on Module 4 Electricity and Magnetism are:
A relationship between current and voltage for a metal is plotted.
If the metal is an ohmic conductor, calculate its resistance.
(A) \(0.60 \ Ω\)
(B) \(0.67 \ Ω\)
(C) \(1.50 \ Ω\)
(D) \(1.70 \ Ω\)
The diagram below shows two long parallel plates that are oppositely charged. A negative test charge \( \text {-q}\) is placed along the dotted line \( \text {XY}\).
Which of the following graphs best represents how the electric potential varies with position as the negative test charge \( \text {-q}\) is moved from \( \text X \) to \( \text Y\)?
An electron is placed at rest between two vertical parallel electric plates as shown below.
Calculate:
(a) The magnitude of the electric field between the plates \( \text {AB}\). (1 mark)
(b) The direction and magnitude of the electric force on the electron. (2 marks)
(c) The time taken for the electron to travel from the plate \( \text A \) to the plate \( \text B\). (3 marks)
(d) The kinetic energy of the electron at plate \( \text B \). (1 mark)
Written by DJ Kim
DJ is the founder of Matrix Education and has over 20 years of HSC Physics teaching experience. He is the co-author of the Matrix Science program, course materials and assessments. He is also renowned for his ATAR & Scaling seminars and development of the first ATAR Calculator.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
