Select a year to see courses
Select a year to see available courses
Want to get better at Year 11 and 12 calculus? This guide covers key concepts, formulas, and strategies; plus free worksheets to help you practise!
Join 75,893 students who already have a head start.
"*" indicates required fields
Join 8000+ students each term who already have a head start on their school academic journey.
Calculus can seem tricky at first, but it’s actually one of the most powerful and exciting parts of Maths! Whether you’re in Year 11 or Year 12, having a strong grasp of calculus is key to doing well in your assessments and the HSC. In this guide, we’ll explain what calculus is, why it matters, and how you can get better at it. You’ll also get a free worksheet with advanced calculus questions to help you practise.
Let’s get into what Year 11 and 12 calculus is all about and how you can level up your skills.
Calculus is a branch of Maths that focuses on change and accumulation. It helps you figure out how things are changing at any moment and how to calculate the total effect of those changes over time or space.
In Year 11 and 12 Maths, calculus builds on the foundations you’ve already learned in algebra, geometry, and functions, but takes them to a more advanced level. Think of it as the maths that powers Physics, Economics, and Engineering.
There are two main parts of Year 11 and Year 12 calculus:
1. Differentiation – measuring change
This is all about understanding rates of change. If you’ve ever wondered how fast something is moving or how steep a hill is, you’re thinking in terms of differentiation. You’ll use it to:
Differentiation tells you the instantaneous rate of change: What’s happening right now, not just over time.
2. Integration – adding up change
Integration is the reverse of differentiation. It helps you calculate totals (or accumulations) of changes. For example:
You’ll learn to apply both indefinite integrals (which give you general rules) and definite integrals (which give you specific values).
Integration is like summing up small pieces over time to get a bigger picture.
Real-world applications
Calculus is used in real life all the time.
Engineers use it to model stress on bridges, design roller coasters, and simulate traffic flow. Physicists use it to predict how objects move, from falling apples to orbiting satellites. Economists use it to optimise costs and revenue. Biologists use it to model population growth or the spread of diseases. Data scientists use it to improve machine learning models and predictions.
Even something as everyday as calculating your mobile data usage over time involves the principles of integration!
If you’re in Year 11 and 12, it’s important to know that calculus isn’t just another Maths topic; it’s a tool that can open doors for your future. Here’s why it matters:
STEM pathways: If you’re planning to study STEM (Science, Technology, Engineering, Mathematics) after school, calculus gives you a strong foundation for university-level learning.
Every day thinking: Calculus is used when you’re modelling costs, rates, populations, and plenty of other data you come across every day.
To get ahead in Maths and do well in calculus, these are the must-know areas:
Remember, differentiation is all about rates of change (how quickly something is happening). Key things you should know how to do:
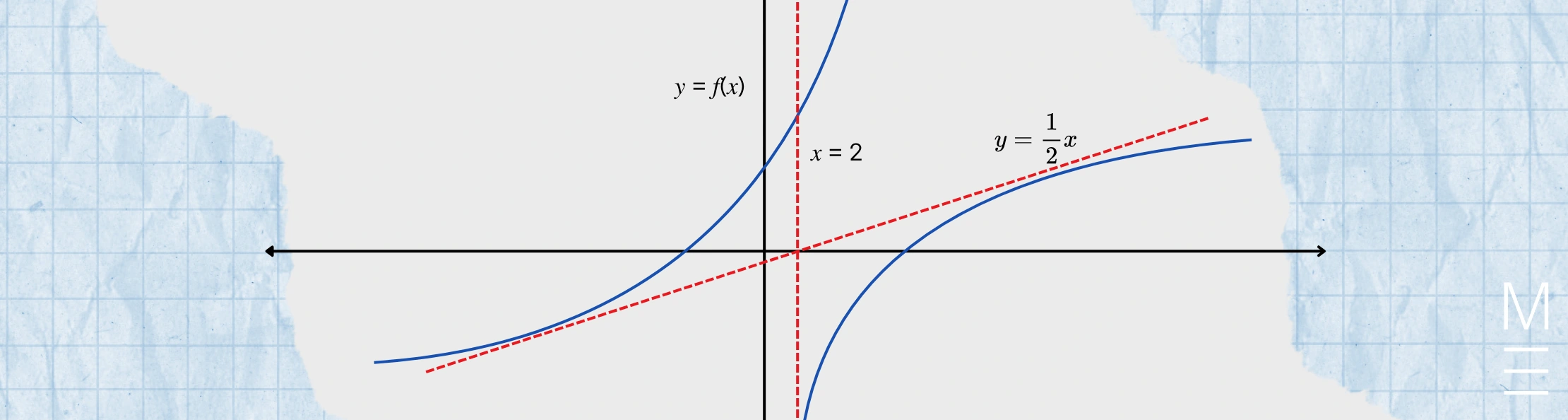
Matrix students use a consistent method, kind of like a mental checklist, to solve differentiation problems accurately and avoid mistakes.
As previously mentioned, integration reverses the process of differentiation. You can expect to:
Many students overlook definite integrals and how to interpret units. These matter in applied questions!
A lot of calculus questions you’ll see in exams are based on real-life scenarios. Some common applications include:
To solve these problems confidently, you need to understand what calculus actually means and how it connects to what’s happening in real life.
A worksheet to test your knowledge. 
Free Year 11 Maths Calculus Worksheet Download
If you’re aiming for a Band 6 or planning to take on Extension Maths, it’s important to go beyond just knowing the basics. Here are a few high-impact strategies to boost your calculus skills:
Even if you’re pretty confident with calculus, it’s easy to fall into habits that can lose you marks without even realising it. Let’s go through some common mistakes students make, so you know what to look out for and how to avoid them.
Skipping steps
It’s tempting to skip steps when you feel confident, especially if the question seems simple. But even small errors (like forgetting a negative sign or mixing up a power) can throw off your entire solution. Writing things out step-by-step helps you stay organised and shows your thinking clearly. It also helps you pick up method marks!
Example:
When finding the derivative of \(x^3 + 2x^2 – x\), you might be tempted to skip steps. This usually leads to errors like missing the correct powers or coefficients.
Write it out as \(\frac{d}{dx}(x^3) + \frac{d}{dx}(2x^2) – \frac{d}{dx}(x)\) to ensure accuracy.
This gives you:
\(3x^2 + 4x – 1\)
Rushing through questions
Calculus questions can be long or have tricky wording. If you rush, you’re more likely to miss key details like limits of integration or whether you’re meant to differentiate or integrate.
Take your time. Read the question carefully and think through your approach before jumping in.
Example:
If a question asks for the area under a curve between \(x = 1\) and \(x = 4\), rushing might cause you to forget to set up the proper definite integral bounds.
Take your time and write the definite integral correctly.
\(\int_{1}^{4} f(x), dx\)
Ignoring how the questions relates to real life
Calculus gets way easier when you connect it to real-world situations. Don’t just focus on crunching numbers; think about what the maths is actually describing. Ignoring these practical uses can make calculus feel abstract and harder to grasp.
Example:
Instead of just solving \(\frac{dy}{dx} = 2x\), picture this as a car speeding up over time, where \(x\) represents time and \(\frac{dy}{dx}\) is the car’s speed (velocity). Thinking of real-world scenarios makes the math more relatable and easier to recall.
Year 11 and 12 calculus might feel challenging, but with the right practice, you’ll get the hang of it. Focus on understanding the key topics, work through problems regularly, and don’t be afraid to ask for help if you get stuck.
Want extra practice? Grab our Advanced Calculus Practice Worksheet for free! It’s packed with challenging questions and step-by-step solutions to help you prepare for Year 12 Maths exams and beyond.
Level up your skills in calculus by taking on these challenging problems!
Written by Matrix Maths Team
The Matrix Maths Team are tutors and teachers with a passion for Mathematics and a dedication to seeing Matrix Students achieving their academic goals.
© Matrix Education and www.matrix.edu.au, 2025. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
