Part 3: Complex Vectors & Loci | Beginner’s Guide to Year 12 Ext 2 Maths

Struggling with complex vectors and loci? Well, you came to the right place! In this article, we will go through everything you need to know about complex vectors and loci and provide you with a worksheet of practice questions.

 

 

In this article, we’ll discuss:

• NESA Syllabus Outcomes
• Assumed Knowledge
• Vector Applications of Complex Numbers
  • Addition and Subtraction of vectors
  • Scaling of Vectors
  • Rotation of Vectors
  • Product and Division of Vectors
• Complex Loci
  • Geometric Approach
  • Algebraic Approach
• The Triangle Inequality
• Reverse Triangle Inequality

 

Practise your complex vectors and loci skills with 4 levels of questions!

 

Year 12 Extension 2 Mathematics: Complex Vectors and Loci

The topic Complex Numbers builds upon the existing knowledge of the real number system and involves the investigation and understanding of the imaginary numbers.

This builds on prior knowledge and applications of algebra and geometry to the complex number system.

The study of Complex Numbers can be used to appreciate mathematics in the real world and is used in physics, engineering and statistics.

 

NESA Syllabus Outcomes

NESA requires students to be proficient in the following outcomes:

 

N2.2: Geometrical implications of complex numbers

• Examine and use addition and subtraction of complex numbers as vectors in the complex plane
  • Given the points representing \(z_1\) and \(z_2\), find the position of the points representing \(z_1 + z_2\) and \(z_1 – z_2\)
  • Describe the vector representing \(z_1 + z_2\) or \(z_1 – z_2\) as corresponding to the relevant diagonal of a parallelogram with vectors representing \(z_1\) and \(z_2\) as adjacent sides
• Examine and use the geometric interpretation of multiplying complex numbers, including rotation and dilation in the complex plane
• Recognise and use the geometrical relationship between the point representing a complex number \(z=a+ib\), and the points representing \(\bar{z}\), \(cz\) (where \(c\) is real) and \(iz\)
• Identify subsets of the complex plane determined by relations, for example \(|z-3i|≤Arg(z)≤\frac{3π}{4}\), \(Re(z)>Im(z)\) and \(|z-1|=2|z-i|\)

 

 

Assumed Knowledge:

Students should feel confident utilising skills like algebra, trigonometry, vectors and geometry using the real number system.

Students should also be familiar with manipulating complex numbers algebraically, as well as expressing them in different forms (Cartesian, Mod-Arg and Exponential forms).

 

 

Introducing Vectors:

Recall from the Extension 1 course that vectors have a magnitude and direction, rather than just a scalar quantity.

Vectors can be added together using the head-to-tail method to obtain the resultant vector.

 

 

Vectors on the Argand Diagram:

The magnitude of the vector is the modulus \(|z|\) of the complex number.

The direction of the vector is the argument \(Arg(z)\) of the complex number.

Given \(z\) is represented by \(\overrightarrow{OA}\) on the Argand Diagram, with modulus \(|z|\) and argument \(θ\), vector \(\overrightarrow{BC}\) is the same vector since it has the same modulus and argument.

Vectors are able to move freely on the Argand-Diagram given the modulus and argument are fixed.

 

 

Addition of Complex Vectors

The vector \(z\), represented by \(\overrightarrow{OA}\) and \(w\), represented by \(\overrightarrow{OB}\) are drawn on the Argand-Diagram.

To add these vectors together, vector \(\overrightarrow{OB}\) can be moved so that the tail of the second vector connects to the head of the first vector \(\overrightarrow{OA}\).

The tail of the first vector is then connected to the head of the second vector, giving the resultant vector \(z+w\).

 

 

 

Subtraction of Complex Vectors

The vector \(z\), represented by \(\overrightarrow{OA}\) and \(w\), represented by \(\overrightarrow{OB}\) are drawn on the Argand-Diagram.

To subtract these vectors together, vector \(\overrightarrow{OB}\) can be flipped.

Use the fact \(z-w=z+(-w)\), then using addition of vectors to find the resultant vector.

 

 

Example 1:

Given \(z=-2+i\) and \(w=4+3i\),

(i) Plot \(z, \ w, \ z+w\) and \(z-w\) on the Argand Diagram

(ii) Find \(z+w\) and \(z-w\) algebraically

 

Solution:

i)

 

ii) \(z+w= 2+ 4i, \ z-w= -6-2i\)

 

 

Scaling Complex Vectors

Vectors can also be scaled by multiplying it with some real number \(k\), where \(k\) is the scaling factor.

• For a positive number \(k\), the resulting vector will have the same direction as the original vector
• For a negative number \(k\), the resulting vector will have the opposite direction as the original vector

 

 

 

 

Rotation of Complex Vectors

Consider a vector \(z\), and vector \(iz\). \(|z|=|iz|\), so the modulus holds true.

The argument of \(z\) is \(arg(z)\), and the argument of \(iz\) is \(arg(iz) = arg(i)+arg(z)= \frac{π}{2}+arg(z)\)

Therefore, when multiplying a vector by \(i\), the resultant vector is rotated by \(\frac{π}{2}\) anticlockwise.

 

Example 2:

Given \(z=1-2i\) and \(w=-2+3i\)

(i) Plot \(z, \ w, \ iz\) and \(-iw\) on the Argand Diagram

(ii) Find \(iz\) and \(-iw\) algebraically

 

Solution:

(i)

 

(ii) \(z=2+i, \ w= 3+2i\)

 

 

Multiplication and Division of Complex Vectors

The multiplication and division of complex vectors can be done by representing vectors in the Mod-Arg form. Recall the following:

• In multiplication, the modulus is multiplied and the argument is added.
• In division, the modulus is divided and the argument is subtracted.

Given vectors \(z=acisα\) and \(w=bcisβ\) are represented on the Argand Diagram, find \(zw\) and \(\frac{z}{w}\)

\begin{align*}
wz &= ab \ cis(α+β)\\
\frac{w}{z} &= \frac{b}{a} cis(β-α)\\
\end{align*}

 

 

Example 3:

Given \(z=1+i\) and \(w=-1+ \sqrt3 i\)

(i) Plot \(w\), \(z\), \(wz\) and \(\frac{w}{z}\) on the Argand Diagram

(ii) Find \(wz\) and \(\frac{w}{z}\) algebraically

 

Solution:

(i)

 

 

(ii)

\begin{align*}
z=\sqrt2cis\frac{π}{4}&, \ w=2cis\frac{2π}{3}\\
zw= 2\sqrt2cis\frac{11π}{12}&, \frac{w}{z} = \sqrt2cis\frac{5π}{12}\\
\end{align*}

 

 

 

 

What is Complex Loci?

The locus of a complex number is the rule imposed on a set of numbers. For example, the locus of complex number  can be a region, curve or set of points. The complex loci can be found geometrically or algebraically, but typically geometrically is the preferred approach.

 

Complex Loci: The Geometric Method

Examples from the Syllabus

 

Example 1:

Find and sketch the locus of \(|z-3i|≤ 4\)

 

Solution:

The distance of \(z\) from \(3i\) is less than or equal to 4

\begin{align*}
|x+(y-3)i|&≤ 4\\
x^2+(y-3)^2 &≤ 16\\
\end{align*}

 

 

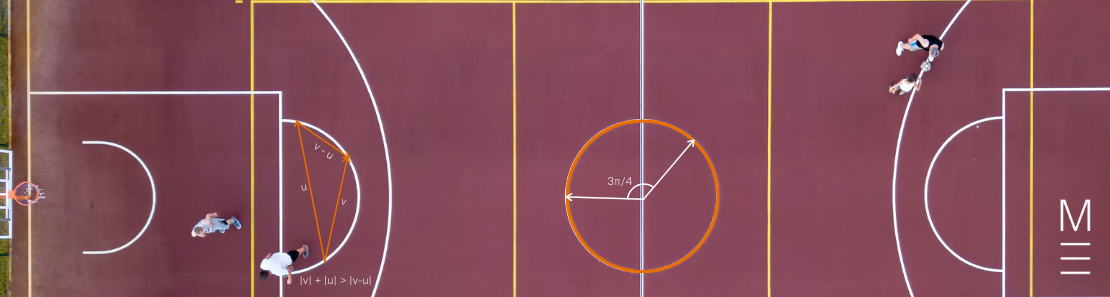
Example 2:

Find and sketch the locus of \( \frac{π}{4} ≤ Arg(z) ≤ \frac{3π}{4} \)

 

Solution:

The argument of  from the origin is between \( \frac{π}{4} \) and \( \frac{3π}{4} \) inclusive

 

 

Example 3:

Find and sketch the locus of \(Re(z)>Im(z)\)

 

Solution

The real values of \(z\) is larger than the imaginary values of \(z\)

\(x>y\)

 

 

Complex Loci: The Algebraic Method

If a question cannot be done geometrically, then the algebraic method is utilised. The steps involve:

1. Let \(z=x+yi\)
2. Simplify equation into Cartesian Form
3. Draw the Cartesian Form on the Argand Diagram

Examples from the Syllabus

 

Example 4:

Find and sketch the locus of \(|z-1|=2|z-i|\)

 

Solution:

\begin{align*}
\text{Let } z&=x+yi\\
|(x-1)+yi|&=2|x+i(y-1)|\\
\sqrt{(x-1)^2+y^2} &= \sqrt{4[x^2+(y-1)^2]}\\
(x+1)^2+(y-2)^2 &=4\\
\end{align*}

 

 

 

Example 5:

Sketch and find the locus of \(arg(z+1)-arg(z-1)=\frac{π}{4}\)

 

Solution:

Draw the points given by \((-1,0)\) and \((1,0)\). As \(\frac{π}{4}\) is an acute angle, it will be a major arc. The arc will be drawn anticlockwise from the first point \((-1,0)\).

 

When given two arguments

 

 

The Triangle Inequality

Recall, that in any given triangle with sides \(a\), \(b\) and \(c\), the following inequalities hold true:

\begin{align*}
a+b &> c\\
b+c &> a\\
c+a &> b\\
\end{align*}

The sum of the lengths of any two sides of a triangle will be larger than the length of the third side.

This can be extended to a triangle on the Argand Diagram:

Let \(\overrightarrow{OP}\) represent \(z_1\), \(\overrightarrow{PQ}\) represent \(z_2\) and \(\overrightarrow{OQ}\) represent \(z_1+z_2\).

 

Then \(|z_1|+|z_2|>|z_1+z_2|\) (the sum of the lengths of two sides of the triangle is larger than the length of the third side). Therefore:

\(|z_1|+|z_2|≥|z_1+z_2|\)

 

 

The Reverse Triangle Inequality

\(||z_1|-|z_2||≤ |z_1+z_2|\)

Recall that the triangle inequality finds the maximum value of the triangle length. The reverse triangle inequality finds the minimum value of the triangle length.

Rather, any side of a triangle is larger than the difference of the other two sides.

 

Example 1:

A complex number \(z\) satisfies \(|z-2 -2i|=2\). Draw the diagram and find the maximum and minimum values of \( |z| \).

 

\( \text{min} = \text{distance from origin to the centre} –   \text{the radius} \sqrt{2^{2} + 2^{2}} – 2 = 2 ( \sqrt{2} – 1 ) \) \( \text{max} = \text{distance from origin to the centre} + \text{the radius} \sqrt{2^{2} + 2^{2}} + 2 = 2 ( \sqrt{2} + 1 ) \)

 

 

Concept Check Questions

Sketch and find the locus of the following:

1. \(|z-8i|=|z-4|\)

2. \(– \frac{π}{4}≤arg(z-2-i)<\frac{π}{6}\)

3. \(arg \left( \frac{z-2}{z} \right) = \frac{π}{2}\)

 

 

Concept Check Solutions

1. \(|z-8i|=|z-4|\)

The distance of \(z\) from \(8i\) is equal to the distance of \(z\) from \(4\)

The two points are \((0,8)\) and \((4,0)\)

 

 

2. \( -\frac{π}{4} ≤ arg(z-2-i)≤ \frac{π}{6}\)

The angle from \((2,i)\) is between \(-\frac{π}{4}\) and \(\frac{π}{6}\) inclusive

 

 

3. \(arg \left( \frac{z-2}{z} \right) = \frac{π}{2}\)

\(arg(z-2)-arg(z) = \frac{π}{2}\)

The angle at the semi-circle is \(\frac{π}{2}\)

The circle has centre \((1,0)\) and radius \(1\)

 

 

Are you struggling to grasp complex Maths Ext 2 concepts?

At Matrix+, our HSC experts break down complex concepts through structured video lessons, provide you with a wide range of comprehensive resources and practice questions, and offer one-to-one help. Learn more now.