Select a year to see courses
Congratulations Year 12 on making it this far into your HSC exam season! You've found the 2022 Maths Advanced HSC Solutions put together by the Matrix Maths Team. Read on to see how you went!
Join 75,893 students who already have a head start.
"*" indicates required fields
In this article, we reveal 2022 HSC Maths Adv Exam Paper Solutions, complete with full explanations written by the Matrix Maths Team.
Have you seen the 2022 HSC Mathematics Advanced exam paper yet? For reference, you can find it, here.
Doing past papers? Find all the solutions to the 2018 – 2022 HSC Maths Adv Exams, here.
Multiple Choice Questions
| Question | Answer | Solution |
| 1. | A | The given equation \(y=-2x+2\) has a gradient of -2. This corresponds to a downward sloping graph, so the solution must be either (A) or (B). The \(y\)-intercept is 2, ∴ (A) is the correct solution – (B) has a negative y-intercept. |
| 2. | D | Old median: The dataset has an even number of scores, so the median is the average of the middle two values given by \(\frac{17+17}{2}=17\). New median: The dataset now has an odd number of scores, so the median is simply the middle value. In this case the middle value is 17, so the median hasn’t changed. Whether the mean is affected can be verified by calculation: |
| 3. | B | \begin{align*} \tan{(26^\circ)}&=\frac{h}{AB}\\ \\ AB&=\frac{h}{\tan{(26^\circ)}}\\ \\ AB&=h\cot{(26^\circ)} \end{align*} |
| 4. | A | Since \(x^2 \geq 0\), subtracting \(1\) from both sides of the inequality gives \(f(x)=x^2-1 \geq -1\). Hence, the range of \(f(x)\) is given by \([-1, \infty)\). |
| 5 | D | Applying the quotient rule on \(h(x)=\displaystyle\frac{f(x)}{g(x)}\), \begin{equation*} The gradient of the tangent to the graph of \(y=h(x)\) at \(x=1\) is evaluated at \(h'(1)\). \begin{align*} |
| 6 | B | \begin{align*} \int\frac{1}{\left(2x+1\right)^2}\ dx&=\int\left(2x+1\right)^{-2}dx\\ &=-\frac{1}{2}\left(2x+1\right)^{-1}+C\\ &=-\frac{1}{2\left(2x+1\right)}+C\\ \end{align*} |
| 7 | C | For a point on a probability density function, the \(x\)-value is the value of the random variable, and the \(y\)-value is the probability that the random variable will have that particular \(x\)-value. The mode is the \(x\)-value with the highest probability, which occurs at the maximum \(y\)-value on the graph. The maximum point on the graph is \(\left(\frac{\pi}{4},\frac{3}{2\pi}\right)\), so the mode is \(x=\frac{\pi}{4}\). |
| 8 | C | It’s given that \(y=f(x)\) is an even function, allowing simplification of the integral: \begin{align*} \int_{-2}^{2}f(x) \ dx&=2\int_{0}^{2}f(x) \ dx\\ \end{align*} The integral can then be computed using the areas of A and B. Region A is above the x-axis so has a positive contribution to the integral, and Region B is below the x-axis so has a negative contribution. \begin{align*} 2\int_{0}^{2}f(x) \ dx&=2(A-B)\\ &=2 \left(\frac{1}{2}-\frac{3}{2}\right)\\ &=-2 \end{align*} |
| 9 | A | Let the probability of winning one of the games be \(x\). By using the complement, \begin{align*} P(\text{winning at least one of the games}) &= 1 – P(\text{losing both games})\\ \\ 0.8 &= 1 – (1-x)^2\\ \\ (1-x)^2 &= 0.2\\ \\ 1-x &= \pm \sqrt{0.2}\\ \\ x &= 1 \pm \sqrt{0.2} \end{align*} Since \(0 \leq x \leq 1\), the only solution is \(x=1-\sqrt{0.2}\). \begin{equation*} P(\text{winning both games})=x^2=0.31 \end{equation*} |
| 10 | B | From the given graphs, \(f(x)\) is symmetric about the \(y\)-axis so it is an even function, i.e. \(f(-x)=f(x)\). Let \(h(x)=g(f(x))\). Then \(h(-x)=g(f(-x))=g(f(x))=h(x)\) meaning that \(h(x) = g(f(x))\) is an even function. Hence, (B) is the only possible correct option as it is the only one with an even function graph. |
(a)
| The value of A can be found by adding the frequency of delivery fee complaints to the cumulative frequency of the previous category (stock storage). \begin{equation*} The value of B can be found by dividing the cumulative frequency of the `Damaged item’ category by the total number of complaints. \begin{equation*} |
(b)
| The line graph on the Pareto chart corresponds to the cumulative percentage, with the values represented by the axis on the right of the chart. The cumulative percentage reaches a value of \(80\%\) within the `Delivery Fee’ category, so \(80\%\) of the complaints are stock shortages and delivery fees. |
(a)
| “Varies inversely with temperature” means that the equation will be of the form \(M=\dfrac{k}{T}\), where \(k\) is a constant. \begin{align*} T &= 15, M = 12 \\ \\ M &= \frac{k}{T} \Longrightarrow 12 = \frac{k}{15} \\ \\ k &= 180 \\ \\ ∴ M &= \frac{180}{T} \end{align*} |
(b)
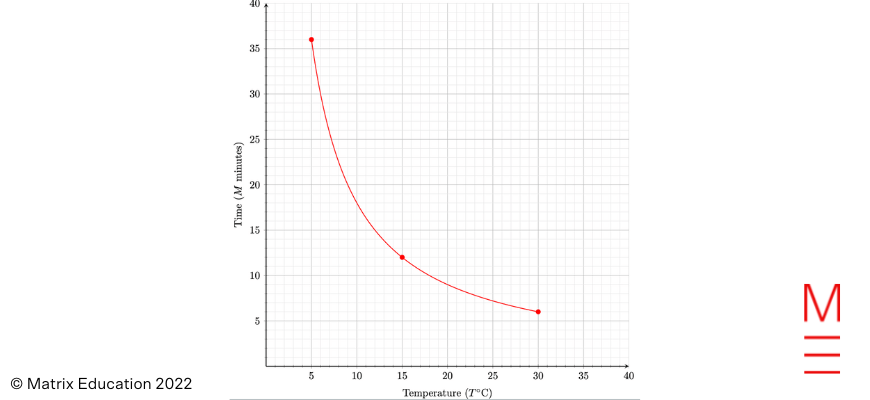
| The values of \(M\) can be calculated by substituting each \(T\) value into \(M=\dfrac{180}{T}\) from part (a). |
| T | 5 | 15 | 30 |
| M | 36 | 12 | 6 |
| The relationship can then be graphed by plotting each of the points from the table. The line connecting the points should be curved, as the relationship \(M=\dfrac{180}{T}\) is in the form of a hyperbola \(y=\dfrac{k}{x}\). \emph{Note}: The question specifies “from \(T=5^\circ C\) to \(T = 30^\circ C\)“, so the graph should not extend past these values. |
| Let \(f(x) = \sqrt{1+x^2} \\\). Using the trapezoidal rule for the given integral: \begin{align*} \int_0^2 \sqrt{1+x^2} \ dx &= \int_0^2 f(x) \ dx \\ \\ &\approx \frac{2-0}{2\times2}\left[f(0) + f(2) + 2f(1)\right] \\ \\ &= \frac{2}{4}\left[1+\sqrt{5}+2\sqrt{2}\right] \\ \\ &= 3.03\ \text{(2 d.p.)} \\ \end{align*} |
| \begin{align*} \text{Amplitude:}\;& k = 4 \\ \text{Period:}\;& 6\pi = \frac{2\pi}{a} \Longrightarrow a = \frac{2\pi}{6\pi}=\frac{1}{3} \end{align*} |
(a)
| \begin{equation*} P(\text{die shows a 5})=\frac{2}{3}\times\frac{1}{6}+\frac{1}{3}\times\frac{3}{6}=\frac{5}{18} \end{equation*} |
(b)
| This is a conditional probability question: “the probability that it is a special die \(\textbf{given that}\) the die shows a 5″ written using probability notation is \(P(\text{special die}\ |\ \text{die shows a 5}) \\\) \begin{align*} P(\text{special die}\ |\ \text{die shows a 5}) &= \frac{P(\text{special die} \cap \text{die shows a 5})}{P(\text{die shows a 5})} \\ \\ &=\frac{P(\text{special die}) \times P(\text{special die shows a 5})}{P(\text{die shows a 5})} \\ \\ &=\frac{\frac{1}{3}\times\frac{3}{6}}{\frac{5}{18}} \\ \\ &=\frac{3}{5} \end{align*} |
(a)
| The line is above the parabola, so the area between them will be given by the integral \(\int^3_{-1} (\text{line}-\text{parabola}) \ dx\). \begin{align*} |
(a)
| The number of cards in each row follows the arithmetic progression \(3, 6, 9, \cdots\), with \(a=T_1=3\) and \(d=3\). \begin{align*} S_n&=\frac{n}{2}\left[2a+d(n-1)\right]\\ S_{12}&=\frac{12}{2}\left[6+3(12-1)\right]=234 \end{align*} |
(b)
| Setting the sum to \(S_n = 828\) and solving for \(n\): \begin{align*} S_n=828&=\frac{n}{2}\left[6+3(n-1)\right] \\ \\ 1656&=n(3+3n) \\ \\ 1656&=3n+3n^2 \\ \\ n^2+n-552&=0 \\ \\ (n+24)(n-23)&=0 \\ \\ n&=-24, 23 \\ \\ ∴ n &= 23 \; \text{rows} \quad (n > 0) \end{align*} |
(a)
| \begin{align*} y’&=4\left(x^2+1\right)^3\times2x\\ \\ &=8x\left(x^2+1\right)^3 \end{align*} |
(b)
| \begin{align*} \frac{d}{dx}\left[\left(x^2+1\right)^4\right]&=8x\left(x^2+1\right)^3\\ \\ \int\frac{d}{dx}\left[\left(x^2+1\right)^4\right] dx&=8\int x\left(x^2+1\right)^3 dx \\ \\ ∴ \int x\left(x^2+1\right)^3 dx &= \frac{1}{8}\int\frac{d}{dx}\left[\left(x^2+1\right)^4\right] dx \\ \\ &=\frac{1}{8}\left(x^2+1\right)^4+C\\ \end{align*} |
The function \(f(x) = x^2\) will have the following transformations:
|
(a)
| \begin{align*} N(0)=200e^{0}=200\ \text{bacteria} \end{align*} |
(b)
| \begin{align*} N(24)&=200e^{24\times0.013}\\ \\ &=200e^{0.312}\\ \\ &\approx 273\ \text{bacteria} \end{align*} |
(c)
| \begin{align*} N'(t)&=200\times0.013e^{0.013t}\\ \\ &=2.6e^{0.013t}\\ \\ N'(24)&=2.6e^{0.312}\\ \\ &=3.55\ \text{bacteria/hour} \end{align*} |
(a)
| Using the future value formula with \(P=40000\), \(r=\dfrac{0.012}{12}=0.001\) and \(n=10 \times 12 = 120\), \begin{align*} \text{Option 1} \; &= 40000\left(1 + 0.001\right)^{120} \\ \\ &= \$45097.17 \end{align*} |
(b)
| Quarterly interest rate \(= \dfrac{0.024}{4} = 0.006 \\\) Number of periods \(= 10 \times 4 = 40 \\\) From the table with \(r=0.006\) and \(N=40\), the future value interest rate is \(45.05630\)\begin{align*} \text{Option 2} \; &= \$1000 \times 45.05630 \\ &= \$45056.30 \end{align*} \begin{align*} \text{Difference} \; &= \$45097.17 – \$45056.30 \\ &= \$40.87 \end{align*} |
| \begin{align*} y&=x^3-6x^2+8\\ \\ y’&=3x^2-12x\\ \\ y”&=6x-12 \end{align*} Setting \(y’=0\) to find the stationary points: \begin{align*} 3x^2-12x=0\\ \\ 3x(x-4)=0\\ \\ x=0\ \text{or}\ x=4\\ \\ ∴ \text{ Stationary points are}\\ \\ (0,8)\ \text{and}\ (4,-24) \end{align*} Testing the nature of of each stationary point: \begin{align*} x=0&: \quad y”=-12 <0 \; ∴ \text{Maximum}\\ \\ x=4&: \quad y”=24-12=12 >0 \; ∴ \text{Minimum}\\ \\ \end{align*} We have now found a local maximum and minimum. The boundary points of the domain also need to be tested to determine the global maximum and minimum value. \begin{align*} \text{At }x&=-1,\ y=1\\ \\ \text{At }x&=7,\ y=57 \end{align*} Neither of the boundary points have a y-value less than -24, so the global minimum is the stationary point \(\left(4,-24\right)\)The boundary point \(\left(7,57\right)\) is the global maximum, as the y-value is greater than the y-value of the local maximum.\begin{align*} ∴ &\text{ Global maximum value is }57\\ \\ &\text{ Global minimum value is }-24\\ \end{align*} |
(a)
| The high and low tide depths correspond to the maximum and minimum values of the equation, which can be found by adding and subtracting the amplitude to the central \(d\)-value (vertical offset). \begin{align*} |
(b)
| For a cosine curve of the form \(y=A\cos{(Bx+C)}+D\), the period is given by \(\dfrac{2\pi}{B}\). \begin{align*} \text{Period }&=\frac{2\pi}{4\pi/25}\\ \\ &=2\pi\times\frac{25}{4\pi}=12.5\\ \\ &=12.5\text{ hours} \end{align*} |
(c)
| Finding the first two times where \(d=1\): \begin{align*} 1.3-0.6\cos\left(\frac{4\pi}{25}t\right)&=1\\ \\ 0.6\cos\left(\frac{4\pi}{25}t\right)&=0.3\\ \\ \cos\left(\frac{4\pi}{25}\right)&=\frac{1}{2}\\ \\ \frac{4\pi}{25}t&=\frac{\pi}{3},\ \frac{5\pi}{3}\\ \\ t&=\frac{25}{12},\frac{125}{12}\\ \end{align*} To verify that the tide is above 1 metre during the interval \(t = \dfrac{25}{12}\) and \(t=\dfrac{125}{12}\), a point in between these values of \(t\) can be tested, or a graph drawn. Testing a point:\begin{align*} \text{at }t=\frac{75}{12} \text{, } d=1.9 \\ \\ 1.9 > 0, ∴ \text{above }1\ m \end{align*}Using a graph: |
| The time between low tides is then the difference between the two values: \begin{align*} =&\frac{125}{12}-\frac{25}{12}\\ \\ =&\frac{25}{3}\\ \end{align*} ∴ the tide will be at a depth of at least 1 metre for \(\dfrac{25}{3}\) hours between successive low tides |
|
| Noting that the domain for \(2x\) is \(0 < 2x < 2\pi\), \begin{align*} f'(x) = 2 \cos(2x) &= -\sqrt{3} \\ \\ \cos(2x) &= -\frac{\sqrt{3}}{2} \\ \\ 2x &= \frac{5\pi}{6}, \frac{7\pi}{6}\\ \\ x &= \frac{5\pi}{12}, \frac{7\pi}{12} \end{align*} and \begin{align*} f”(x) = -4 \sin(2x) &= 2 \\ \\ \sin(2x) &= -\frac{1}{2} \\ \\ 2x &= \frac{7\pi}{6}, \frac{11\pi}{6}\\ \\ x &= \frac{7\pi}{12}, \frac{11\pi}{12} \end{align*} The only solution for which \(f'(x) = -\sqrt{3}\) AND \(f”(x) = 2\) is \(x = \dfrac{7\pi}{12}\). |
| Split the range 820-920 at the mean to produce two sub-ranges: 820-840 and 840-920. For \(840-920 \\\): The empirical (68-95-99.7) rule states that \(68\%\) lies within 1 standard deviation away from the mean. So, \(\frac{68}{2} = 34\%\) lie between \(840-920\). For \(820-840 \\\): Since normal distributions are symmetric, then \(50\%\) lie below the mean of \(840\). So, \(60 \%-50 \% = 10\%\) lie between \(840-860\). Again due to symmetry about the mean, this means \(10\%\) lie between \(820-840\). Overall: ∴ \(34 \% + 10 \% = 44\%\) lie between \(820-920\) hours. |
(a)
| \begin{align*} f”(x)&=-2e^{-2x}-2\left(e^{-2x}+(-2)xe^{-2x}\right)\\ \\ &=-2e^{-2x}-2\left(e^{-2x}-2xe^{-2x}\right)\\ \\ &=-2e^{-2x}-2e^{-2x}+4xe^{-2x}\\ \\ &=4xe^{-2x}-4e^{-2x}\\ \\ &=4(x-1)e^{-2x} \end{align*} |
(b)
| The stationary points are where \(f'(x)=0\): \begin{align*} f'(x)=e^{-2x}-2xe^{-2x}&=0\\ \\ e^{-2x}(1-2x)&=0 \end{align*} Since \(e^{-2x} \neq 0\), \begin{align*} 1-2x&=0\\ x&=\frac{1}{2}\\ \end{align*} The nature can be found from the second derivative \(f”(x) \\\): \begin{align*} f”\left(\frac{1}{2}\right)&=4\left(\frac{1}{2}-1\right)e^{-1}\\ \\ &\approx -0.74 \end{align*} \begin{align*} ∴ x = \frac{1}{2} \text{ is a local maximum as } f”\left(\frac{1}{2}\right)<0 \end{align*}\(y\)-value is:$$y=f\left(\frac{1}{2}\right) = \frac{1}{2e}, \text{and so}$$ \begin{align*} ∴ \left(\frac{1}{2},\frac{1}{2e}\right) \text{ is a local maximum} \end{align*} |
(c)
| We are sketching the curve \(y = f(x) = xe^{-2x}\). For the \(x\)-intercepts, let \(y = 0\): \begin{align*} 0 &= x e^{-2x} \\ \\ ∴ x &= 0 \quad (e^{-2x} \neq 0) \end{align*} For the \(y\)-intercepts, let \(x = 0\): \[y = f(0) = 0 \times e^{0} = 0\] To find the point of inflection, we find the solutions of \(f”(x) = 0\). \begin{align*} 4(x-1)e^{-2x} &= 0 \\ \\ ∴ x &= 1 \quad (e^{-2x} \neq 0) \end{align*} |
| \(x\) | 0 | 1 | 2 |
| \(f”(x)\) | – | 0 | + |
| Since there is a change of concavity, \(\left(1,\dfrac{1}{e^2}\right)\) is a point of inflection. Finally, before we sketch we will note the limiting behaviour. \begin{align*} &\text{As } x \to -\infty: \quad y \to -\infty \\ &\text{As } x \to +\infty: \quad y \to 0^+ \end{align*} |
(a)
| From the diagram, \(\tan \theta = \frac{1}{1} = 1\) and so \(\theta = \dfrac{\pi}{4}\). Noting that the radius of the circle is \(r = \sqrt{2}\), \begin{align*} \text{Shaded Region} &= \text{Area of Sector}-\text{Area of Triangle} \\ \\ &= \pi \times \left(\sqrt{2}\right)^2 \times \frac{\pi / 4}{2\pi} – \frac{1}{2} \times 1 \times 1 \\ \\ &= \frac{\pi}{4} – \frac{1}{2} \ u^2 \end{align*} |
(b)
| Substitute the origin \((0, 0)\) into the hyperbola \(y = \dfrac{a}{b-x}-1\): \begin{equation} 0 = \frac{a}{b} – 1 \Longrightarrow a = b \end{equation} Substitute the point \((1, 1)\) into the hyperbola \(y = \dfrac{a}{b-x}-1\): \begin{equation} 1 = \frac{a}{b-1} – 1 \Longrightarrow 2 = \frac{a}{b-1} \end{equation} Substitute equation \((1)\) into equation (2) and solving simultaneously: \begin{align*} 2 &= \frac{a}{a-1} \\ 2(a-1) &= a \\ 2a-2 &= a \\ a &= 2 \end{align*} Since \(a = b\) from equation \((1)\), then it follows that \(a=b=2\). |
| The region bounded by the hyperbola, the positive \(x\)-axis and the circle is equivalent to the sum of the area below the hyperbola from \(x=0\) to \(x=1\) and the shaded area from part (a). \begin{align*} \text{Total Area} &= \int_0^1 \frac{2}{2-x} – 1 \ dx + \text{Shaded Area from part (a)} \\ \\ &= \Big[ -2\ln|2-x| – x \Big]_0^1 + \frac{\pi}{4} – \frac{1}{2} \\ \\ &= -2\ln1 – 1 – (-2\ln2-0) + \frac{\pi}{4} – \frac{1}{2} \\ \\ &= 2\ln2 +\frac{\pi}{4} – \frac{3}{2} \end{align*} |
(a)
| The areas of the rectangle form the geometric series \(1, \dfrac{1}{2}, \dfrac{1}{4}, \dfrac{1}{8}, \cdots\), where the first term is \(a=1\) and the common ratio is \(r=\dfrac{1}{2}\). Since \(|r| < 1\), the limiting sum of this geometric series exists and is given by: |
(b)
| From the reference sheet, we can apply the formula, \begin{equation*} \int f'(x) a^{f(x)} = \frac{a^{f(x)}}{\ln a} + c \end{equation*}with \(a=2\), \(f(x)=-x\) and \(f'(x)=-1\).\begin{align*} \int_0^4 2^{-x} \ dx &= – \int_0^4 – 2^{-x} \ dx \\ \\ &= – \left[ \frac{2^{-x}}{\ln2}\right]_0^4\\ \\ &= -\frac{1}{\ln 2} (2^{-4} -1 ) \\ \\ &= \frac{15}{16 \ln 2} \end{align*} |
(c)
| The area under the exponential from \(x=0\) to \(x=4\) is less than the limting sum of the areas of the rectangle. \begin{align*} \int_0^4 2^{-x} \ dx &< S_{\infty} \\ \frac{15}{16 \ln 2} &< 2 \quad (\text{from parts (a) and (b)}) \\ \\ 15 &< 32 \ln 2 = \ln 2^{32} \\ \\ e^{15} &< 2^{32} \end{align*} |
(a)
| \begin{align*} F(e^3) &= 1 \\ \\ \frac{1}{k} \ln e^3 &= 1 \\ \\ 3\ln e &= k \\ \\ k &= 3 \end{align*} |
(b)
| Since \(X\) is a continuous random variable, then \(P(X \leq c) = P(X < c)\). Now taking the complement, we have: \begin{align*} P(X < c) &= 2P(X > c) \\ \\ &= 2 \left[ 1 – P(X \leq c) \right]\\ \\ &= 2 \left[ 1 – P(X < c) \right]\\ \\ &= 2 – 2P(X < c) \\ \\ 3 P(X < c) &= 2 \\ \\ P(X < c) &= \frac{2}{3} \end{align*} Recall that the cumulative distribution function can be expressed as \(F(x) = P(X < x)\). \begin{align*} F(c) &= \frac{2}{3} \\ \\ \frac{1}{3} \ln c &= \frac{2}{3} \\ \\ \ln c &= 2 \\ \\ ∴ c &= e^2 \end{align*} |
(a)
| Since \(P\), \(X\) and \(Y\) all lie on the same line, then the gradients between any two of these points must be equal. \begin{align*} m_{YX} &= m_{XP} \\ \\ \frac{y-0}{0-x} &= \frac{0-2}{x-1} \\ \\ -\frac{y}{x} &= – \frac{2}{x-1} \\ \\ y &= \frac{2x}{x-1} \end{align*} |
(b)
| Let \(A\) denote the area of \(\triangle XOY\). The area of the triangle can be written in terms of \(x\) by substituting the result from part (a): \begin{align*} A &=\frac{1}{2}xy \\ \\ &= \frac{1}{2}x\times\frac{2x}{x-1}\\ \\ &=\frac{x^2}{x-1} \end{align*} The minimum value of the area can be found by differentiating and finding the minimum stationary point. \begin{align*} \frac{dA}{dx} &=\frac{2x(x-1)-x^2\times1}{(x-1)^2}\\ \\ &=\frac{2x^2-2x-x^2}{(x-1)^2}\\ \\ &=\frac{x^2-2x}{(x-1)^2}\\ \\ &=\frac{x(x-2)}{(x-1)^2} \end{align*} To find the stationary points: \begin{align*} \frac{dA}{dx} &=0\\ \\ \frac{x(x-2)}{(x-1)^2}&=0\\ \\ x&=0, 2\\ \end{align*}The question specifies that \(x>1\), ∴ \(x = 2\). Testing the nature of the stationary point:
∴ The stationary point at \(x=2\) is a minimum. |
(a)
| The terms within the brackets after \(M\) follow a geometric progression, with \(a=1\), \(r=1.0025\) and \(n\) terms, so the amount owing, \(A_n\), can be simplified using the formula for the sum of a geometric progression. \begin{align*} A_n&=P(1.0025)^n-M\left(1+(1.0025)^1+(1.0025)^2+…+(1.0025)^{n-1}\right)\\ \\ A_n&=P(1.0025)^n-M\times\frac{1\left(1.0025^n-1\right)}{1.0025-1}\\ \\ A_n&=P(1.0025)^n-M\left(\frac{1.0025^n-1}{0.0025}\right) \end{align*} The question states that the loan is to be repaid in 180 payments, meaning that \(A_{180}=0\), and \(P\) is given as \(200 000\). \begin{align*} A_{180}=0&=200000(1.025)^{180}-M\left(\frac{1.0025^{180}-1}{0.0025}\right)\\ \\ M\left(\frac{1.0025^{180}-1}{0.0025}\right)&=200000(1.025)^{180}\\ \\ M&=\frac{200000(1.0025)^{180}\times0.0025}{1.0025^{180}-1} \\ \\ M&=1381.16 \end{align*} |
(b)
| The amount owing when the interest rate changes is \($100 032\), so the new \(P=100032\). The interest rate has changed from \(0.25\%\) to \(0.35\%\), so \(r=1.0035\). The monthly repayments have remained the same, so \(M=1381.16\).The new amount owing, \(B_n\), takes the same form as before, but with the new values of \(P\) and \(r\).\begin{equation*} B_n = P(1.0035)^n – M \left( \frac{1.0035^n-1}{0.0035} \right) \end{equation*} Jane makes regular payments until there is no money left owing, so we are interested in finding \(n\) such that \(B_n=0\). \begin{align*} 0&=P(1.0035)^n-M\left(\frac{1.0035^n-1}{0.0035}\right)\\ \\ 0&=P(1.0035)^n-\frac{M}{0.0035}(1.0035)^n+\frac{M}{0.0035}\\ \\ (1.0035)^n\left(\frac{M}{0.0035}-P\right)&=\frac{M}{0.0035}\\ \\ 1.0035^n&=\frac{M}{0.0035}\div\left(\frac{M}{0.0035}-P\right)\\ \\ 1.0035^n&=\frac{1381.16}{0.0035}\div\left(\frac{1381.16}{0.0035}-100032\right)\\ \\ 1.0035^n&=1.3396\\ \\ n&=\frac{\ln{1.3396}}{\ln{1.0035}}=83.67 \end{align*} The question asks for how many full monthly payments Jane needs to make, so the solution is \(83\) months. |
(c)
| The final repayment will be equal to the amount owing after the last full repayment is made, with interest applied. From part (b), Jane will make \(83\) full repayments before the final repayment, so the amount owing is \(B_{83}\): \begin{align*} B_{83}&=100032(1.0035)^{83}-1381.16\left(\frac{1.0035^{83}-1}{0.0035}\right)\\ \\ B_{83}&=928.29 \end{align*} Interest then needs to be applied, as it is calculated at the end of the month, before the repayment is made: \begin{align*} \text{Final Repayment} &= 928.29\times1.0035\\ \\ &= \$931.54 \end{align*} |
Written by Matrix Maths Team
The Matrix Maths Team are tutors and teachers with a passion for Mathematics and a dedication to seeing Matrix Students achieving their academic goals.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
