Welcome to Matrix Education
To ensure we are showing you the most relevant content, please select your location below.
Select a year to see courses
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Select a year to see available courses
Science guides to help you get ahead
Science guides to help you get ahead


Our Year 10 Maths resources are designed by subject matter experts and cover all aspects of the new NSW Maths syllabus. Get ahead with 150+ pages of content, 100+ pages exam-style practice questions, quizzes, and a topic test for each module.

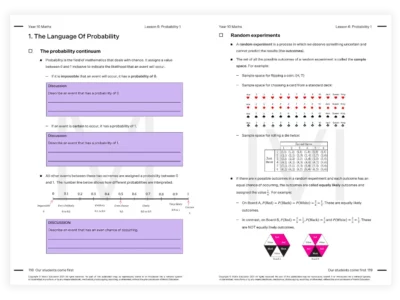


Develop in-depth understanding and fluency in mathematics by applying our proven methods for Maths. Solve new, unfamiliar maths questions at school with confidence.

Step 1
Theory
Step 2
Application
Step 3
Guided Examples
Step 4
In-Class Practice
Step 5
Homework
Step 6
Videos for Revision
Step 7
Quizzes & Feedback
Stay informed at every step of your child’s academic journey with the Matrix Learning Management System (LMS), designed to intelligently track homework progression and achievement.
Select an option below to see how our flexible learning methods can cater for your learning needs.
Overview
Term Course overview
Overview
Term Course overview
Audience
Who it's for
Audience
Who it's for
Program
What's covered
Program
What's covered
Benefits
What you'll gain
Benefits
What you'll gain
Approach
How it works
Approach
How it works
Overview
The Matrix Year 10 Maths Term Course is a structured 9-week program where students learn the full next term’s content before it is taught at school, giving them a clear head start and greater confidence. Through 9 weekly 1.5-hour lessons, students build mastery in key topics including Quadratic Equations, Trigonometry, Curve Sketching, Functions, Polynomials, and Logarithms. Each lesson combines clear explanations, worked examples, and guided practice with weekly quizzes, feedback, and exam-style homework.
With small class sizes, structured resources, and a deliberate progression of topics, the Year 10 Maths Term Course ensures that students not only stay ahead of the school curriculum but also refine their problem-solving, strengthen reasoning skills, and prepare effectively for exams.
Course Timeline
2025 Year 9 students will begin their Year 10 Maths course in October 2025 as Matrix teaches one term ahead of school.
| Period | Matrix Term | Grade at School | Topic Name |
|---|---|---|---|
| Oct – Dec | Term 1 | Year 9 | Quadratic Equations, Probability |
| Jan – Mar | Term 2 | Year 10 | Further Trigonometry |
| Apr – Jun | Term 3 | Year 10 | Curve Sketching, Functions and Relations |
| Jul – Sep | Term 4 | Year 10 | Polynomials and Logarithms |
What’s Included
1. 9 Weekly Lessons
Expert-led classes delivering the full term’s content in structured 1.5-hour sessions
2. Printed Theory Book & Work Book
NSW curriculum-aligned resource with worked examples and practice questions
3. Weekly Homework with Marking and Feedback
Homework is collected each week, marked by tutors, and returned with feedback to reinforce key concepts and address areas for improvement.
4. Matrix Learning Portal Access
Online quizzes, video lessons, and extra practice for independent study
5. Small Class Sizes
Small classes (capped at 15) to ensure individualised attention and support
6. 1:1 Workshop
Free one-on-one tutor support for conceptual understanding or homework assistance
Audience
This course is ideal for students who:
Parents can feel confident that their child is building the skills needed for senior mathematics success.
All students complete an entry test to ensure correct placement.
Program
October – December (Matrix Term 1): Quadratic Equations, Probability
Lesson 1: Quadratic Equations 1
Lesson 2: Quadratic Equations 2
Lesson 3: Quadratic Equations 3
Lesson 4: Quadratic Equations 4
Lesson 5: Quadratic Equations 5
Lesson 6: Probability 1
Lesson 7: Probability 2
Lesson 8: Probability 3
Lesson 9: Review and Topic Test
January – Mar h (Matrix Term 2): Further Trigonometry
Lesson 1: Further Trigonometry 1
Lesson 2: Further Trigonometry 2
Lesson 3: Further Trigonometry 3
Lesson 4: Further Trigonometry 4
Lesson 5: Further Trigonometry 5
Lesson 6: Further Trigonometry 6
Lesson 7: Further Trigonometry 7
Lesson 8: Further Trigonometry 8
Lesson 9: Review and Topic Test
April – June (Matrix Term 3): Curve Sketching, Functions and Relations
Lesson 1: Curve Sketching 1
Lesson 2: Curve Sketching 2
Lesson 3: Curve Sketching 3
Lesson 4: Curve Sketching 4
Lesson 5: Curve Sketching 5
Lesson 6: Curve Sketching 6
Lesson 7: Curve Sketching 7
Lesson 8: Functions and Relations
Lesson 9: Review and Topic Test
July – September (Matrix Term 4) Polynomials and Logarithms
Lesson 1: Polynomials 1
Lesson 2: Polynomials 2
Lesson 3: Polynomials 3
Lesson 4: Polynomials 4
Lesson 5: Sketching Polynomials 1
Lesson 6: Sketching Polynomials 2
Lesson 7: Logarithms 1
Lesson 8: Logarithms 2
Lesson 9: Review and Topic Test
Benefits
Approach
Structured Acceleration
Across 9 weeks, students complete the full next term’s content before it is taught at school. This proactive approach gives them the advantage of familiarity and confidence when topics appear in class or assessments.
Teaching Methods
Each lesson is delivered by experienced teachers using clear explanations, step-by-step worked examples, and explicit instruction. Students then apply their learning through guided practice, weekly quizzes, and exam-style homework that is collected, marked, and returned with feedback.
Content Mix
Lessons focus on teaching upcoming syllabus content in depth while reinforcing foundational skills. Each session balances conceptual understanding with practical application to exam-style problems, ensuring students can transfer knowledge confidently.
Course Progression
Each week builds on the last, following a deliberate sequence of topics. Regular quizzes and reviews help track progress, while workshops provide additional support. By the end of the term, students are well prepared for school assessments and confident in applying their skills.
Matrix teachers are experts in their field with vast classroom teaching experience and HSC and/or university teaching experience.
Get 150+ pages of expertly designed Year 10 Maths content backed by over 30 years of collective teaching experience.
Our small classes are arranged in a U-shape, creating an interactive and engaging learning environment.
Enjoy additional one-on-one tutor support for extra feedback, writing development, or homework assistance.
All Matrix Campuses are designed for student comfort and engagement. Make learning enjoyable with our comfortable and professional learning environment.
Learn from the best. Each Theory Lesson is accompanied by online video lessons led by experienced teachers.
Track your child’s progress and achievement through weekly homework and in-class quizzes.
Review your understanding with the end of term Topic Test performed under strict exam-style conditions in preparation for school assessments.
Get year round access to Theory Lesson Videos, online resources, and track your progress easily via the Matrix LMS platform.
Want advice on your child’s learning? Get exclusive access to academic advice, and invitations to events and seminars from the Matrix academic team.
Enjoy access to all course resources until the end of the academic year.
All on campus courses come with our First Lesson Money Back Guarantee.
Castle Hill
| Tue | 4:30pm - 6:00pm |
| Wed | 4:30pm - 6:00pm |
| Sat | 10:30am - 12:00pm |
| Sun | 9:00am - 10:30am |
| 1:00pm - 2:30pm |
Chatswood
| Tue | 6:10pm - 7:40pm |
| Wed | 6:10pm - 7:40pm |
| Thu | 6:10pm - 7:40pm |
| Fri | 4:30pm - 6:00pm |
| 6:10pm - 7:40pm | |
| Sat | 9:00am - 10:30am |
| 1:00pm - 2:30pm | |
| Sun | 9:00am - 10:30am |
| 2:30pm - 4:00pm | |
| 4:10pm - 5:40pm |
Epping
| Mon | 4:30pm - 6:00pm |
| Thu | 4:30pm - 6:00pm |
| Sat | 10:30am - 12:00pm |
| 2:30pm - 4:00pm | |
| 6:00pm - 7:30pm | |
| Sun | 1:00pm - 2:30pm |
| 4:10pm - 5:40pm |
Hurstville
| Mon | 6:10pm - 7:40pm |
| Wed | 4:30pm - 6:00pm |
| Sun | 9:00am - 10:30am |
| 1:00pm - 2:30pm | |
| 2:30pm - 4:00pm |
Parramatta
| Mon | 6:10pm - 7:40pm |
| Tue | 4:30pm - 6:00pm |
| Fri | 6:10pm - 7:40pm |
| Sat | 6:00pm - 7:30pm |
| Sun | 9:00am - 10:30am |
| 10:30am - 12:00pm | |
| 2:30pm - 4:00pm | |
| 4:10pm - 5:40pm |
Strathfield
| Tue | 4:30pm - 6:00pm |
| Fri | 4:30pm - 6:00pm |
| Sun | 10:30am - 12:00pm |
| 1:00pm - 2:30pm |
Sydney City
| Sat | 2:30pm - 4:00pm |
Overview
Holiday Course overview
Overview
Holiday Course overview
Audience
Who it's for
Audience
Who it's for
Program
What's covered
Program
What's covered
Benefits
What you'll gain
Benefits
What you'll gain
Approach
How it works
Approach
How it works
Overview
The Matrix Year 10 Maths Holiday Course is a short, focused program that helps students consolidate key skills, strengthen problem-solving, and build confidence for upcoming school assessments. Each program targets a core area of the NSW Year 10 Mathematics syllabus such as Quadratic Relationships, Trigonometry, Non-Linear Relationships, Polynomials, and Logarithms, giving students the structured practice and expert support they need to succeed.
Across 4 days × 2 hours, students revise essential concepts, practise problem-solving strategies, and receive guidance from experienced teachers. With a balance of explicit instruction, worked examples, and guided practice, they develop the fluency, accuracy, and confidence to begin the next term ready for success.
Course Timeline
| Period | Grade at School | Topic Name |
|---|---|---|
| January | Year 10 | Quadratic Equations |
| April | Year 10 | Essentials of Trigonometry |
| July | Year 10 | Logarithms |
| October | Year 10 | Yearly Exam Preparation Course |
What’s included
1. 4-Day Intensive Program
Two-hour lessons each day targeting a key maths skill area
2. Comprehensive Skills Booklet
NSW syllabus-aligned resources with theory, examples, and practice problems
3. Daily In-Class Practice
Worked solutions and guided revision tasks for each topic
4. Small Class Sizes
Personalised attention and support from expert teachers
Audience
This course is ideal for Year 10 students who:
Need structured revision to consolidate key topics
Want to reinforce skills in algebra, trigonometry, and logarithms
Are preparing for exams with focused practice and expert guidance
Benefit from small-class teaching and step-by-step problem-solving
It is also ideal for parents seeking a productive, academically focused holiday program.
Program
January – Mastering Quadratics
Day 1: Quadratic Equations 1
Day 2: Quadratic Equations 2
Day 3: Quadratic Equations 3
Day 4: Quadratic Equations 4
April – Further Trigonometry
Day 1: Trigonometry 1
Day 2: Trigonometry 2
Day 3: Trigonometry 3
Day 4: Trigonometry 4
July – Logarithms (Extension Path)
Day 1: Logarithms 1
Day 2: Logarithms 2
Day 3: Logarithms 3
Day 4: Logarithms 4
October – Yearly Exam Preparation Course
Day 1: Quadratic Equations, Probability
Day 2: Further Trigonometry
Day 3: Curve Sketching, Functions and Relations
Day 4: Logarithms
Benefits
1. Core concept mastery
Step-by-step explanations of key Stage 5 topics
2. Problem-solving fluency
Guided examples and practice to apply concepts with accuracy
3. Exam readiness
Structured revision that mirrors school assessment demands
4. Confidence and independence
Strategies to tackle new problems effectively under time pressure
Approach
Structured Revision
In just 4 days, students revise weeks of school content with greater clarity and focus. The intensive format allows them to immerse in mathematics without the interruptions of a regular term timetable.
Content Focus
Each course consolidates essential skills from the previous term while sharpening key areas such as Quadratic Relationships, Trigonometry, Non-Linear Relationships, Polynomials, and Logarithms. This ensures students are prepared for upcoming topics and assessments.
Teaching Approach
Lessons are led by expert Maths teachers and combine explicit instruction, step-by-step problem solving, and worked examples. Students then apply their learning through guided practice tasks that build fluency, accuracy, and confidence.
Daily Progression
Each day builds on the last, starting with revision of fundamentals and moving into more advanced applications. This sequence reinforces learning and ensures students leave the course ready to succeed in the new term.
Matrix teachers are experts in their field with vast classroom teaching experience and HSC and/or university teaching experience.
Our small classes are arranged in a U-shape, creating an interactive and engaging learning environment.
All Matrix Campuses are designed for student comfort and engagement. Make learning enjoyable with our comfortable and professional learning environment.
Chatswood
| 19 - 22 Jan |
| 11:00am - 1:00pm |
Parramatta
| 19 - 22 Jan |
| 11:00am - 1:00pm |
Strathfield
| 12 - 15 Jan |
| 9:00am - 11:00am |
Learn at your own pace with the support you need. Work through your Matrix Theory Book with 8 clear video lessons taught by experienced Matrix teachers.

Address gaps in learning by asking questions on the student Q&A board to receive individual teacher support within 1 working day.
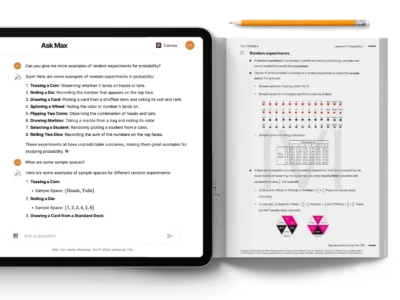
Enrolled students get instant explanations, personalised feedback, and step-by-step solutions anytime with their AI study companion, Ask Max.

Complete exam-style questions in your Work Book, online quizzes, and end-of-term Topic Tests to consolidate key concepts and build exam confidence.
Module 1
Quadratic Equations, Probability
Module 1
Quadratic Equations, Probability
Module 2
Further Trigonometry
Module 2
Further Trigonometry
Module 3
Curve Sketching, Functions and Relations
Module 3
Curve Sketching, Functions and Relations
Module 4
Polynomials and Logarithms
Module 4
Polynomials and Logarithms
Module 1
Lesson 1: Quadratic Equations 1
Lesson 2: Quadratic Equations 2
Lesson 3: Quadratic Equations 3
Lesson 4: Quadratic Equations 4
Lesson 5: Quadratic Equations 5
Lesson 6: Probability 1
Lesson 7: Probability 2
Lesson 8: Probability 3
Lesson 9: Review and Topic Test
Module 2
Lesson 1: Further Trigonometry 1
Lesson 2: Further Trigonometry 2
Lesson 3: Further Trigonometry 3
Lesson 4: Further Trigonometry 4
Lesson 5: Further Trigonometry 5
Lesson 6: Further Trigonometry 6
Lesson 7: Further Trigonometry 7
Lesson 8: Further Trigonometry 8
Lesson 9: Review and Topic Test
Module 3
Lesson 1: Curve Sketching 1
Lesson 2: Curve Sketching 2
Lesson 3: Curve Sketching 3
Lesson 4: Curve Sketching 4
Lesson 5: Curve Sketching 5
Lesson 6: Curve Sketching 6
Lesson 7: Curve Sketching 7
Lesson 8: Functions and Relations
Lesson 9: Review and Topic Test
Module 4
Lesson 1: Polynomials 1
Lesson 2: Polynomials 2
Lesson 3: Polynomials 3
Lesson 4: Polynomials 4
Lesson 5: Sketching Polynomials 1
Lesson 6: Sketching Polynomials 2
Lesson 7: Logarithms 1
Lesson 8: Logarithms 2
Lesson 9: Review and Topic Test
Matrix teachers are experts in their field with vast classroom teaching experience and HSC and/or university teaching experience.
Get 150+ pages of expertly designed Y10 Maths content backed by over 30 years of collective teaching experience delivered right to your doorstep.
Currently enrolled students can access Max, their personal AI study buddy, anytime for feedback, explanations, or help with tricky questions — available on the Matrix LMS platform.
Learn from the best. Each Theory Lesson is accompanied by online video lessons led by experienced teachers.
Get regular practice and feedback with weekly homework and online quizzes.
Stuck on a question? Address individual learning needs using the Q&A boards and receive teacher responses within 1 working day.
Review your understanding with the end of term Topic Test performed under strict exam-style conditions in preparation for school assessments.
Get year round access to Theory Lesson Videos, online resources, and track your progress easily via the Matrix LMS platform.
Enjoy the flexibility of online learning with all the benefits of being on-campus. Lesson content progression is automatically unlocked for the best learning experience, ensuring students stay on track for success.
Enjoy access to all course resources until the end of the year.
Want advice on your child’s learning? Get exclusive access to academic advice, and invitations to events and seminars from the Matrix academic team.
Online
| Access starts | 13 October 2025 |
| Access Ends | 31 December 2026 |
Matrix+ online
Term course
Holiday course
Who is it for?
Course structure
Matrix resources
Reporting
Additional support
Homework
Assessments





















years teaching
Qualifications
Year levels
Subjects taught
Years at Matrix
years
Teaching experience
years
Campuses
Locations
Teaching methods
Flexible payment options: Pay quarterly or monthly over 3 months.
Term Course
9 weekly lessons over 9 weeks
$702
per term
$234
per month for 3 months
Holiday Course
4 daily lessons over 4 days
$358
per holiday course
N/A
Matrix+ online
9 lessons, anywhere, anytime
$420
per module
$140
per month for 3 months
The structured lessons with quizzes and question time for homework really helped consolidate my knowledge as well as learn from my classmates.

Tara Anglican School for Girls
Especially as Maths starts to get more difficult moving into senior years, Matrix covers the Year 10 content thoroughly to ensure that you have a good foundation for Year 11 and 12 concepts. Matrix helped me to feel more confident in my Maths skills as I moved into senior school.

Sydney Girls High School
Revising content for a second time in Matrix, alongside or even before learning them in school helped me to consolidate that knowledge and remember concepts easier.

Sydney Girls High School
The Matrix Math Course helped me to solve Maths problems faster than before. It also allowed me understand the core concepts of how equations work and how each formula was developed.

Cheltenham Girls High School (1958)
Matrix Maths Courses really helped consolidate my understanding and knowledge for Maths and also helped me build on the skills required for senior years.

St George Girls' High School
With Maths, the main thing was being on top of content, and Matrix allows you to do that a term early! Being a Matrix Maths student has been extremely helpful to my grades and confidence in a difficult subject.

Sydney Girls High School
Who are Matrix Year 10 Maths teachers?
All Matrix Year 10 Maths teachers are experienced educators who possess degrees in Secondary Education or Mathematics-related disciplines. Our Maths experts are knowledgeable, qualified, and have the real teaching experience necessary to explain concepts clearly whilst making learning engaging and enjoyable for young learners.
How do Matrix teachers teach Year 10 Maths?
Matrix Year 10 Maths teachers deliver a structured and engaging secondary Maths tutoring experience through a mix of direct instructional and interactive teaching. All Matrix Year 10 Maths tutoring courses include high-quality resources designed to provide students and teachers with proven methods for critical thinking, reasoning, and problem-solving.
Does the Matrix Year 10 Maths course follow the NSW school syllabus?
Yes, the Matrix Year 10 Maths course thoroughly covers the new NSW Education Standards Authority (NESA) Maths Syllabus. The course helps students develop strong foundations in all aspects of Maths, ensuring students are confident and well-prepared at school.
Will the course match what my child is learning at school?
Matrix teaches Maths one term ahead of the school curriculum, with Year 10 Term 1 starting in October while students are still in Year 9. This means students learn in advance, gain a competitive advantage over their school peers, and reinforce their understanding and confidence when the topic is revisited at school.
Does the program prepare my child for Stage 6 Mathematics?
Yes. The Matrix Years 7-10 Maths tutoring courses are designed to build the strong foundations needed for success in Year 11 Mathematics Advanced, and Year 11 Mathematics Extension 1.
Can the tutoring course improve my child's marks at school?
Yes. Parents consistently report that their child’s confidence and marks improve two terms after enrolling in the Matrix Year 10 Maths course. Our combination of expert teaching, structured learning, and ongoing feedback helps students achieve stronger school results.
How many students are in a Matrix Year 10 Maths class?
Matrix classes are capped at 15 students per class, seated in a U-shaped layout to encourage participation, peer discussion, and teacher-student interaction.
How long is each Matrix Year 10 Maths tutoring lesson?
Each Year 10 Maths tutoring lesson runs for 1.5 hours and consists of Theory, Application, and In-Class Practice.
How is my child’s progress tracked?
Student progress is tracked through weekly homework review, classroom participation, and performance in quizzes and topic tests. Teachers provide verbal and written feedback to support improvement. Parents can view student progress on our Matrix Learning Management System (LMS).
If a student needs extra help, they can get instant academic support via our AI-powered Chatbot or attend optional Workshops for personalised guidance.
If my child misses a Year 10 Maths lesson, how can they catch up?
Students gain access to Matrix Theory Tutorial Videos on our Matrix Learning Management System (LMS), which contains the same content covered in-class. Videos are paired with the Matrix Theory Book and Work Book, allowing students to review lessons at home, and return to class prepared.
How is the Matrix Holiday course different from the Matrix Term course?
The Year 10 Maths Holiday Intensive is a short, 4 day focused program designed for high-impact revision of Year 10 Maths topics. Each Holiday program consolidates key concepts from the previous term while sharpening core skills in Quadratic Relationships, Further Trigonometry, Non-Linear Relationships, Polynomials and Logarithms to set students up for success in the upcoming term assessments.
The Term course develops skills gradually across several weeks, allowing time for deeper learning, extended practice, and steady improvement.
Should my child enrol in both the Holiday and Term course?
For best results, yes. The Year 10 Maths Term course builds foundational knowledge over several weeks. The Holiday course complements this by consolidating learning in a concentrated format, allowing students to revise their skills. Many families enrol in both to ensure their child masters the content and identifies areas for improvement.
What should my child bring to class?
Students should bring a pencil case, water bottle, a calculator, and a readiness to learn. All other learning resources are provided on the first day of class.
What is Matrix+?
Matrix+ is an online Year 10 Maths tutoring course consisting of on-demand Theory Tutorial Videos paired with a Matrix Theory Book and Work Book. It is a flexible, accessible, affordable, and self-paced alternative to Matrix on-campus tutoring.
Does my child need to attend Matrix+ at a set time?
No. Year 10 Maths Matrix+ students can watch on-demand video tutorials anytime and anywhere. Students can pause, replay, or speed up videos, making it an accessible and flexible learning experience for all types of learners.
Which Year 10 Maths courses can my child complete on Matrix+?
Students have the flexibility to complete multiple Year 10 Maths courses at the same time. They can also enrol into past Term courses to review lessons or catch up on missed content.
How long will my child have access to the Matrix+ course?
Year 10 Maths students begin their Matrix+ online course on the first day of the Matrix Term. They can access all Theory Tutorial Videos, Q&A Discussion Boards, and online resources until 31 December of the Matrix academic year. For example, students enroled in the Year 10 Maths Matrix+ course for Term 1 (beginning in October) will have access until the end of the following calendar year.