For those of you eager to see how you went, the Matrix Maths Team has put together solutions for the 2022 HSC Maths Extension 1 Exam. Read on to see how you went!
Join 75,893 students who already have a head start.
"*" indicates required fields
In this article, we reveal 2022 HSC Maths Ext 1 Exam Paper Solutions, complete with full explanations written by the Matrix Maths Team.
Have you seen the 2022 HSC Mathematics Extension 1 exam paper yet? For reference, you can find it here.
Doing past papers? Find all the solutions to the 2018 – 2022 HSC Maths Ext 1 Exams here.
| Question | Answer | Solution |
| 1 | C | The range of \(y=\cos^{-1} x\) is \(0 \leq y \leq \pi\). Since \(\frac{23 \pi}{12}\) does not fall within this range, we want to find a corresponding angle within the range. Applying the property \(\cos x = \cos(2 \pi – x)\), we have: \begin{align*} \cos \frac{23 \pi}{12} &= \cos \left( 2\pi – \frac{23 \pi}{12}\right) \\ \\ &= \cos \frac{\pi}{12}\\ \\ ∴ \cos^{-1} \left( \frac{\sqrt{6}+\sqrt{2}}{4}\right) &= \cos^{-1} \left( \cos \frac{23 \pi}{12}\right)\\ \\ &= \cos^{-1} \left( \cos \frac{\pi}{12}\right)\\ \\ &= \frac{\pi}{12} \end{align*} |
| 2 | A | Noting that both \(f(x)\) and \(g(x)\) have the exact same graph for \(x \geq 0\), the only transformation which retains this information is \(g(x) = f(|x|)\). |
| 3 | D | The degree of the divisor is always greater than the degree of the remainder, and the degree of the remainder \(2x+5\) is \(1\). Therefore, the degree of \(Q(x)\) must be strictly greater than \(1\), so the degree could be \(2\) but not necessarily must be \(2\). |
| 4 | A | Observing carefully at the the positive \(x\)-intercept for \(y=f(x)+g(x)\), only the addition of graphs in option (A) satisfies this \(x\)-intercept. |
| 5 | B | \begin{equation*} y = 3-2t^2 = 3-2(x-2)^2 \end{equation*} This equation is the concave down parabola \(y=-2x^2\) shifted right by 2 units and up by 3 units. Therefore, the curve is a concave down parabola with vertex at \((2, 3)\) which matches option (B). |
| 6 | B | Since the diagram is drawn to scale, we can approximate \(\tilde{u}\approx \tilde{i} + 2\tilde{j}\).
The projection of \(\tilde{u}\) onto \(\tilde{i}+\tilde{j}\) is given by: |
| 7 | C | There are \(12\) chosen points on the triangle, of which \(3\) must be chosen to form a triangle. The number of combinations using any \(3\) points is \(\dbinom{12}{3} = 220\). However, a triangle cannot be formed by \(3\) collinear points.
Therefore, there are \(220-1-4-10=205\) triangles that can be formed using the chosen points. \(a_{i}\) |
| 8 | D | Since we are working with vectors and are given an angle \(\theta\) between the two unit vectors \(\tilde{a}\), \(\tilde{b}\), we will aim towards expressing \(|\tilde{a} + \tilde{b}|\) using dot products. Beginning with \(0 \leq |\tilde{a} + \tilde{b}| < 1\): \begin{align*} 0 & \leq |\tilde{a} + \tilde{b}| < 1 \\ 0 & \leq |\tilde{a} + \tilde{b}|^2 < 1 \\ 0 & \leq (\tilde{a} + \tilde{b}) \cdot (\tilde{a} + \tilde{b}) < 1 \\ 0 & \leq \tilde{a} \cdot \tilde{a} + 2(\tilde{a} \cdot \tilde{b}) + \tilde{b} \cdot \tilde{b} < 1 \\ 0 & \leq |\tilde{a}|^2 + 2(\tilde{a} \cdot \tilde{b}) + |\tilde{b}|^2 < 1 \\ 0 & \leq 1 + 2(\tilde{a} \cdot \tilde{b}) + 1 < 1 \quad (\text{given } |\tilde{a}| = |\tilde{b}| = 1)\\ -2 & \leq 2(\tilde{a} \cdot \tilde{b}) < -1 \\ -1 & \leq \tilde{a} \cdot \tilde{b} < -\frac{1}{2} \end{align*} We can express the angle between two vectors as \[\cos \theta = \frac{\tilde{a} \cdot \tilde{b}}{|\tilde{a}| \cdot |\tilde{b}|} = \tilde{a} \cdot \tilde{b}\] since \(|\tilde{a}| = |\tilde{b}| = 1\). Hence our inequality is \[-1 \leq \cos \theta < -\frac{1}{2}.\] To find an inequality for \(\theta\), we can consider a sketch of \(y = \cos \theta\) to find the range of \(\theta\) that corresponds to \(-1 \leq \cos \theta < – \frac{1}{2}\). 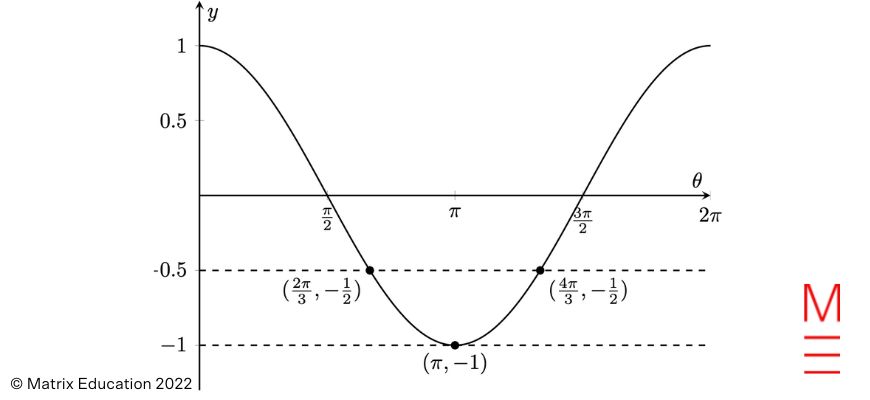 The allowable range for \(\theta\) is \(\frac{2\pi}{3} < \theta < \frac{4\pi}{3}\).All other options fall outside this range, so the only possible correct option is (D). |
| 9 | D | Consider the function \(f(x) = -x\) with inverse function \(f^{-1}(x) = -x\).
Hence, the only possible correct option is (D). |
| 10 | B | Using the property \(\sin x = \cos \left( \frac{\pi}{2} – x \right)\), we have \begin{align*} \sin y + 1 &= \cos \left( \frac{\pi}{2} – y \right) + 1 \\ \\ &= 2 \cos^2 \left( \frac{\pi}{4} – \frac{y}{2} \right) – 1 + 1, \quad \text{(using the double angle formula on cosine)}\\ \\ &= 2 \cos^2 \left( \frac{\pi}{4} – \frac{y}{2} \right) \end{align*} Now, solving the differential equation, \begin{align*} \frac{dy}{dx} &= \sin y + 1 \\ \\ \frac{dy}{dx} &= 2 \cos^2 \left( \frac{\pi}{4} – \frac{y}{2} \right) \\ \\ \int \frac{dy}{2 \cos^2 \left( \frac{\pi}{4} – \frac{y}{2} \right)} &= \int dx \\ \\ \frac{1}{2} \int \sec^2 \left( \frac{\pi}{4} – \frac{y}{2} \right) dy &= x+C\\ \\ – \tan \left( \frac{\pi}{4} – \frac{y}{2} \right) &= x+C \\ \\ \frac{\pi}{4} – \frac{y}{2} &= \tan^{-1} [-(x+C)] \\ \\ \frac{y}{2} &= \frac{\pi}{4} – \tan^{-1} [-(x+C)] \\ \\ y &= \frac{\pi}{2} – 2 \tan^{-1} [-(x+C)] \\ \\ y &= \frac{\pi}{2} + 2 \tan^{-1} (x+C), \quad (\text{using the property } \tan^{-1} (-\theta) = -\tan^{-1} \theta) \end{align*} This is an inverse tangent graph vertically dilated by a factor of \(2\) and shifted up by \(\frac{\pi}{2}\) which matches option (B). |
(a)
(i)
| \begin{align*} \tilde{u} + 3 \tilde{v}&= \tilde{i} – \tilde{j} + 3(2\tilde{i} + \tilde{j}) \\ \\ &= 7 \tilde{i} + 2 \tilde{j} \end{align*} |
(ii)
| \begin{align*} \tilde{u} \cdot \tilde{v}&= (\tilde{i}-\tilde{j}) \cdot (2\tilde{i} + \tilde{j}) \\ \\ &= 1 \times 2 + (-1) \times 1 \\ \\ &= 1 \end{align*} |
(b)
| \begin{align*} %\int_0^1 \frac{x}{\sqrt{x^2+4}}dx\\ \\ \text{Let }u &= x^2 + 4 \\ \\ du &= 2x\ dx \\ \\ \frac{1}{2} du &= x dx \end{align*} Finding the new limits of the integral: \begin{align*} \text{at }x = 1, u = 5 \\ \text{at }x = 0, u = 4 \end{align*} \begin{align*} \int_0^1 \frac{x}{\sqrt{x^2+4}}dx &= \frac{1}{2}\int_4^5 \frac{1}{\sqrt{u}}du\\ \\ &=\frac{1}{2}\left[2\sqrt{u}\right]^5_4\\ \\ &=\left[\sqrt{u}\right]^5_4 \\ \\ &=\sqrt{5}-2 \end{align*} |
(c)
| The general term for this binomial expansion is: \begin{align*} T_k&={8\choose k}(1)^{8-k}\left(-\frac{x}{2}\right)^k\\ \\ &={8\choose k}\left(-\frac{1}{2}\right)^kx^k\\ \\ ∴ \text{Coefficient of } x^k &= {8\choose k}\left(-\frac{1}{2}\right)^k \end{align*} \begin{align*} \text{Coefficient of }x^2 &= {8\choose 2}\left(-\frac{1}{2}\right)^2=7\\ \\ \text{Coefficient of }x^3 &= {8\choose 3}\left(-\frac{1}{2}\right)^3=-7 \end{align*} |
(d)
| As the vectors \(\tilde{u}\) and \(\tilde{v}\) are perpendicular, their dot product must equal 0. \begin{align*} \begin{pmatrix}a\\2\end{pmatrix} \cdot \begin{pmatrix}a-7\\4a-1\end{pmatrix}=0&\\ \\ a(a-7)+2(4a-1)=0&\\ \\ a^2-7a+8a-2=0&\\ \\ a^2+a-2=0&\\ \\ (a-1)(a+2)=0&\\ \\ ∴ a = 1\text{ or }a = -2& \end{align*} |
(e)
| \begin{align*} \sqrt{3} \sin x – 3 \cos x &= R \sin(x + \alpha) \\ \\ &= R \sin x \cos \alpha + R \sin \alpha \cos x \\ \\ \color{red}{\sqrt{3}} \sin x-{\color{red}3} \cos x &= \color{red}{R} \color{red}{\cos \alpha} \sin x-\color{red}{R} \color{red}{\sin \alpha} \cos x \end{align*}Equating coefficients of \(\sin x\) and \(\cos x\) gives two equations \begin{equation} R\cos{\alpha}=\sqrt{3} \end{equation} \begin{equation} R\sin{\alpha}=-3 \end{equation} We can find \(R\) by squaring both (1) and (2), then summing together: \begin{align*} R^2\sin{\alpha}^2&=9\\ \\ R^2\cos{\alpha}^2&=3\\ \\ R^2\left(\sin{\alpha}^2+\cos{\alpha}^2\right)&=3+9\\ \\ R^2&=12\\ \\ ∴ R&=2\sqrt{3} \end{align*} We can substitute \(R\) into (1) and (2) to produce \begin{gather*} \sin{\alpha}=-\frac{\sqrt{3}}{2}\text{, }\cos{\alpha}=\frac{1}{2} \end{gather*} Since \(\sin \alpha < 0\) and \(\cos \alpha > 0\), this implies that \(\alpha\) lies in the 4th quadrant. We can solve for \(\alpha\) by considering (2) \(\div\) (1), \begin{align*} \tan{\alpha}&=\frac{\sin{\alpha}}{\cos{\alpha}}\\ \\ \tan{\alpha}&=\frac{-3}{\sqrt{3}}\\ \\ \tan{\alpha}&=-\sqrt{3} \end{align*} \[∴ \alpha =-\frac{\pi}{3} \text{ since } \alpha \text{ lies in the 4th quadrant}\] \begin{gather*} ∴ \sqrt{3}\sin{x}-3\cos{x}=2\sqrt{3}\sin{\left(x-\frac{\pi}{3}\right)} \end{gather*} |
(f)
| First note that our inequality, \(\dfrac{x}{2-x} \geq 5\), has \(2-x\) as the denominator.
So \(x \neq 2\) (this will be important later). Next, we multiply both sides of the inequality by \((2-x)^2\) and rearrange,
∴ \(0\geq(2-x)(5-3x)\) is true for x in the interval \(\left[\dfrac{5}{3}, 2\right]\) Recall that we have the additional restriction that \(x \neq 2\). ∴ The solution is \(x = \) \(\left[\frac{5}{3},\ 2\right)\) or \(\frac{5}{3}\leq x<2\) |
(a)
First, we calculate the derivative at points \(P\), \(Q\) and \(R\):
We can then draw in the slopes at points \(P\), \(Q\) and \(R\):
|
(b)
| Splitting the 41 players (pigeons) over the age limit into the 13 teams (pigeonholes), we get \(\dfrac{41}{13} \approx 3.1538\). Therefore, by the pigeonhole principle, at least one team must have at least 4 players over the age limit. Hence, at least one team will be penalised. |
(c)
| Note to Students: \(\arctan\) and \(\tan^{-1}\) are interchangeable.
We will need to use the product rule to differentiate \(y = x \tan^{-1}x\). \begin{alignat*}{2} |
(d)
(i)
| Since \(12^\circ\mathrm{C}\) is room temperature, then we have the constant \(T_1 = 12\). \begin{align*} \frac{dT}{dt}&=k\left(T-T_1\right)\\ \\ &=k(T-12)\\ \\ \int\frac{dT}{T-12}&=\int k\ dt\\ \\ \ln{|T-12|}&=kt+C\\ \\ T-12&=e^{kt+C}\\ \\ T&=12+Ae^{kt} \end{align*} \begin{align*} \text{At }t=0\text{, }T&=92:\\ \\ 92&=12+Ae^0\\ \\ ∴ A&=80\\ \\ T&=12+80e^{kt}\\ \\ \text{At }t=5\text{, }T&=76:\\ \\ 76&=12+80e^{5k}\\ \\ e^{5k}&=\frac{64}{80}\\ \\ e^{5k}&=\frac{4}{5}\\ \\ 5k&=\ln\left(\frac{4}{5}\right)\\ \\ k&=\frac{1}{5}\ln\left(\frac{4}{5}\right) \end{align*} \begin{gather*} ∴ T=12+80e^{\frac{t}{5}\ln\left(\frac{4}{5}\right)}\\ \end{gather*} |
(ii)
| \begin{align*} 57&=12+80e^{\frac{t}{5}\ln\left(\frac{4}{5}\right)}\\ \\ \frac{9}{16}&=e^{\frac{t}{5}\ln\left(\frac{4}{5}\right)}\\ \\ \ln\left(\frac{9}{16}\right)&=\frac{t}{5}\ln\left(\frac{4}{5}\right)\\ \\ t&=\frac{5\ln\left(\frac{9}{16}\right)}{\ln\left(\frac{4}{5}\right)}=12.89\\ \\ ∴ t&\approx 13\text{ minutes} \end{align*} |
(e)
The expected score of selecting 1 ball is \(E(X) = 3-3.5 = -0.5\). Therefore, the expected score of selecting 4 balls is \(4\times(-0.5) = -2\). |
(f)
| We begin with the base case \((n = 0)\) for induction: \[15^0+6^1=7\text{, which is divisible by }7\] Assume that the statement holds for \(n = k\) where \(k \geq 0\), \[15^k + 6^{2k+1} = 7M, \quad \text{where } M \text{ is an integer}\] We can rearrange to make \(15^k\) the subject for future use, \[15^k = 7M – 6^{2k+1}\] Next, we will prove that the statement holds for \(n = k+1\) as well, i.e. for some integer \(Q\), \[15^{k+1} + 6^{2(k+1)+1} = 7Q\] \begin{align*} \mathrm{LHS} &= 15^{k+1} + 6^{2k+3} \\ \\ &=15(15^k)+6^2(6^{2k+1})\\ \\ &=15\left(7M-6^{2k+1}\right)+36\left(6^{2k+1}\right)\qquad\text{(From assumption for } n = k\text{)}\\ \\ &=7(15M)-15\left(6^{2k+1}\right)+36\left(6^{2k+1}\right)\\ \\ &=7(15M)+21\left(6^{2k+1}\right)\\ \\ &=7\left(15M+3\left(6^{2k+1}\right)\right)\\ \\ &=7Q,\ \text{where }Q \text{ is an integer} \end{align*}∴ By mathematical induction the statement is true for all integers \(n\geq 0\). |
(a)
| \begin{align*} \overrightarrow{BH} \cdot \overrightarrow{CA} &= (\tilde{h}-\tilde{b}) \cdot (\tilde{a} – \tilde{c})\\ &=(\tilde{a} +\tilde{b} + \tilde{c}-\tilde{b}) \cdot (\tilde{a}-\tilde{c})\\ &= (\tilde{a} + \tilde{c}) \cdot (\tilde{a} – \tilde{c})\\ &= \tilde{a} \cdot \tilde{a}-\tilde{c} \cdot \tilde{c}\\ &= |\tilde{a}|^2 – |\tilde{c}|^2\\ &= 0, \quad (\text{since } |\tilde{a}|=|\tilde{c}| \text{ as they are both radii of the same circle}) \end{align*} Therefore, \(\overrightarrow{BH}\) and \(\overrightarrow{CA}\) are perpendicular. |
(b)
| \begin{align*} V&=\pi\int_0^{\mbox{\(\frac{\pi}{2k}\)}}\left(k+1\right)^2\sin^2kx\ dx\\ \\ &=\pi(k+1)^2\int_0^{\mbox{\(\frac{\pi}{2k}\)}}\frac{1}{2}\left[1-\cos\left(2kx\right)\right]\ dx\\ \\ &=\frac{\pi}{2}(k+1)^2\left[x-\frac{\sin{2kx}}{2k}\right]_0^{\mbox{\(\frac{\pi}{2k}\)}}\\ \\ &=\frac{\pi}{2}(k+1)^2\left[\left(\frac{\pi}{2k}-\frac{\sin{\pi}}{2k}\right)-\left(0-\frac{\sin{0}}{2k}\right)\right]\\ \\ &=\frac{\pi}{2}(k+1)^2\left(\frac{\pi}{2k}\right)\\ \\ &=\frac{\pi^2}{4k}(k+1)^2\\ \\ \end{align*}Given that \(V=\pi^2\):\begin{align*} \frac{\pi^2}{4k}(k+1)^2&=\pi^2\\ \\ \frac{\left(k+1\right)^2}{4k}&=1\\ \\ k^2+2k+1&=4k\\ \\ k^2-2k+1&=0\\ \\ (k-1)^2&=0\\ \\ ∴ k&=1 \end{align*} |
(c)
| If \(f\) and \(g\) were inverses, then we should expect that \(g(f(x)) = x\) for all real values of \(x\). However, if we consider \(x=\pi\) which exists on function \(f\), \begin{align*} g(f(\pi)) &= \arcsin \left(\sin(\pi)\right) \\ &= \arcsin \left(0\right) \\ &= 0 \neq \pi \end{align*} Hence, \(g\) is not the inverse of \(f\).Remark: We can also note that the domain of \(f(x)\) and range of \(g(x)\) are different and so they cannot be inverses. |
(d)
| It is given that \(P\) is monic and of degree 3, so it will have the form \(P(x) = x^3+bx^2+cx+d\). We are asked to find \(\alpha\beta +\alpha\gamma+\beta\gamma\), which, using the sum of roots in pairs, is \(c\).
\begin{align*} Using the given fact \(P'(\alpha)+P'(\beta)+P'(\gamma) = 87\): \begin{align*} Substituting the sum of roots and using the fact that \(\alpha^2+\beta^2+\gamma^2 = 85\): \begin{align*} To find the value of \(b^2\): \begin{align*} \begin{align*} |
(e)
(i)
| Let \(X\) be the random variable for the number of chocolate bars that weigh at least 150 g. We can express the desired probability \(\mathcal{P}\) as \[\mathcal{P} = P(X \leq 8)\] We have \(X \sim \mathrm{Bin}(16, 0.8)\) where the mean \(\mu\) and variance \(\sigma^2\) are calculated as follows,\begin{align*} \mu &= np\\ &=16\times0.8\\ &=12.8\\ \sigma^2&=np(1-p)\\ &=16\times0.8\times0.2\\ &=2.56 \end{align*}Let \(Y\) be the normally distributed random variable we will use to approximate \(X\), so we have \[Y \sim \mathcal{N}(12.8, 2.56)\] Applying continuity correction for the normal approximation of the binomial distribution: \[\mathcal{P} = P(X\leq8) \approx P(Y\leq8.5)\] Finding the \(z\)-score of \(8.5\):\begin{align*} z&=\frac{x-\mu}{\sigma}\\ \\ &=\frac{8.5-12.8}{\sqrt{2.56}}\\ \\ &=2.6875 \end{align*}\begin{align*} ∴ P(X\leq8.5)=P(Z\leq-2.6875) \\ \\ \end{align*}where \(Z\) has a standard normal distribution. Using the \(z\)-score table for \(z=-2.69\) (2 d.p.):\begin{align*} ∴ \mathcal{P} = 0.0026 \end{align*} |
(ii)
| For the normal distribution to be a good approximation of the binomial distribution, it is required that \(np>5\) and \(n(1-p)>5\). \begin{gather*} np=16\times0.8=12.8\\ n(1-p)=16\times0.2=3.2\\ \\ 3.2\leq 5\text{, } ∴\text{ The normal approximation may not be valid.} \end{gather*} |
| We will solve this by the method of separation of variables. \begin{align*} (x-2) \frac{dy}{dx} &= xy \\ \\ \frac{dy}{y} &= \frac{x}{x-2} dx \\ \\ \int \frac{dy}{y} &= \int \frac{x-2+2}{x-2} \ dx \\ \\ \int \frac{dy}{y} &= \int 1 + \frac{2}{x-2} \ dx \\ \\ \ln |y| &= x + 2\ln|x-2| + C \end{align*} Substituting \((0, 1)\) into the equation, \begin{align*} \ln |1| &= 0 + 2\ln|0-2| + C \\ \\ C &= -2\ln2 \end{align*} Therefore, the equation becomes \begin{align*} \ln |y| &= x + 2\ln|x-2| -2\ln2 \\ \\ \ln |y| &= \ln e^x + \ln|x-2|^2 – \ln2^2 \\ \\ \ln |y| &= \ln \frac{e^x (x-2)^2}{4}, \quad (x-2)^2 \geq 0 \\ \\ |y| &= \frac{e^x (x-2)^2}{4} \end{align*}Noting that \(e^x > 0\) and \((x-2)^2 \geq 0\), the RHS of the equation is positive. Hence, we are allowed to remove the absolute value signs around \(y\), so the particular solution to the differential equation is: \begin{equation*} y = \frac{e^x (x-2)^2}{4} \end{equation*} |
(b)
| Given that the projection is \(\lambda_0 \vec{v}\) and applying the projection formula, \begin{align*} \vec{p} &= \text{Proj}_{\vec{v}} \vec{u} \\ \\ \lambda_0 \vec{v} &= \frac{\vec{u} \cdot \vec{v}}{|\vec{v}|^2} \vec{v}\\ \\ ∴ \lambda_0 &= \frac{\vec{u} \cdot \vec{v}}{|\vec{v}|^2} \end{align*}Now, consider the expansion of \(|\vec{u}-\lambda \vec{v}|^2-|\vec{u}-\lambda_0 \vec{v}|^2\):\begin{align*} |\vec{u}-\lambda \vec{v}|^2-|\vec{u}-\lambda_0 \vec{v}|^2 &= (\vec{u}-\lambda \vec{v}) \cdot (\vec{u}-\lambda \vec{v})-(\vec{u}-\lambda_0 \vec{v}) \cdot (\vec{u}-\lambda_0 \vec{v}) \\ \\ &= \vec{u} \cdot \vec{u}-2\lambda \vec{u} \cdot \vec{v} + \lambda^2 \vec{v} \cdot \vec{v}-(\vec{u} \cdot \vec{u}-2 \lambda_0 \vec{u} \cdot \vec{v} + \lambda_0^2 \vec{v} \cdot \vec{v}) \\ \\ &=-2 \lambda \vec{u}\cdot \vec{v} + \lambda^2 |\vec{v}|^2 + 2 \lambda_0 \vec{u} \cdot \vec{v}-\lambda_0^2 |\vec{v}|^2\\ \\ &= |\vec{v}|^2 (\lambda^2-\lambda_0^2)-2 \vec{u}\cdot \vec{v} (\lambda-\lambda_0) \\ \\ &= |\vec{v}|^2 (\lambda-\lambda_0)(\lambda + \lambda_0)-2 \vec{u}\cdot \vec{v} (\lambda-\lambda_0) \\ \\ &= |\vec{v}|^2 (\lambda-\lambda_0) \left[ (\lambda + \lambda_0)-2 \frac{\vec{u}\cdot \vec{v}}{|\vec{v}|^2}\right]\\ \\ &= |\vec{v}|^2 (\lambda-\lambda_0) [\lambda + \lambda_0-2\lambda_0], \quad \text{since } \lambda_0 = \frac{\vec{u} \cdot \vec{v}}{|\vec{v}|^2}\\ \\ &= |\vec{v}|^2 (\lambda-\lambda_0)^2 \\ \\ &\geq 0, \quad \text{since } |\vec{v}|^2 \geq 0 \text{ and } (\lambda-\lambda_0)^2 \geq 0 \end{align*} This can be rearranged to \begin{align*} |\vec{u}-\lambda_0 \vec{v}|^2 &\leq |\vec{u}-\lambda \vec{v}|^2 \\ \\ |\vec{u}-\lambda_0 \vec{v}| &\leq |\vec{u}-\lambda \vec{v}| \end{align*} and hence we deduce that \(|\vec{u}-\lambda \vec{v}|\) is minimised when \(\lambda = \lambda_0\). |
(c)
| For the projectile: \begin{align*} x_P&=2ut\cos{\theta}\\ y_P&=2ut\sin{\theta}-\frac{g}{2}t^2 \end{align*} The range of the projectile is equal to the \(x\)-value once it has reached the ground, so to find an expression for the range, let \(y_P=0\) and solve for \(t\), which is greater than 0. \begin{align*} 2ut\sin{\theta}-\frac{g}{2}t^2&=0\\ \\ t\left(2u\sin{\theta}-\frac{g}{2}t\right)&=0\\ \\ 2u\sin{\theta}&=\frac{g}{2}t \\ \\ t&=\frac{4u\sin{\theta}}{g} \end{align*} Substituting this value of \(t\) into \(x_P\) gives the range \(R\) of the projectile: \begin{align*} R&=2u\left(\frac{4u\sin{\theta}}{g}\right)\cos{\theta}\\ \\ &=\frac{8u^2\sin{\theta}\cos{\theta}}{g}\\ \\ &=\frac{4u^2\sin{2\theta}}{g} \end{align*} The maximum range occurs at \(\theta=45^\circ\) when \(\sin{2\theta}=1\): \begin{align*} ∴ R_{\mathrm{max}}=\frac{4u^2}{g} \end{align*} For the projectile to hit the target, we want \(R=x_P=x_T\) at \(t=\dfrac{4u \sin \theta}{g}\). \begin{align*} x_P&=x_T\\ \\ R &= d+ut\\ \\ \frac{4u^2\sin{2\theta}}{g}&=d+\frac{4u^2\sin{\theta}}{g}\\ \\ d&=\frac{4u^2\sin{2\theta}}{g}-\frac{4u^2\sin{\theta}}{g}\\ \\ d&=\frac{4u^2}{g}\left(\sin{2\theta}-\sin{\theta}\right)\\ \\ d&=R_{\mathrm{max}}\left(\sin{2\theta}-\sin{\theta}\right) \end{align*} The greatest value of \(d\) will be when \((\sin{2\theta}-\sin{\theta})\) is maximised. Let \(f(\theta) = \sin{2\theta}-\sin{\theta}\). \begin{align*} &f'(\theta)=2\cos{2\theta}-\cos{\theta} \end{align*} Finding the turning points: \begin{align*} 2\cos{2\theta}-\cos{\theta}&=0\\ \\ 2\left(2\cos^2\theta-1\right)-\cos{\theta}&=0\\ \\ 4\cos^2\theta-\cos{\theta}-2&=0\\ \\ \cos{\theta}&=\frac{1\pm\sqrt{1-4(4)(-2)}}{8}\\ \\ \cos{\theta}&=\frac{1\pm\sqrt{33}}{8}\\ \\ \theta&=32^\circ 32′,\quad 126^\circ 23′ \end{align*} Since \(0 < \theta < 90^\circ\), as \(\theta\) is the angle to the horizontal, so \(\theta = 32^\circ 32′\). Testing for maximum: \begin{align*} f”(\theta) &= -4\sin 2\theta +\sin \theta \\ \\ f”(32^\circ 32′) &\approx -3.089 < 0 \end{align*} Therefore, \(f(\theta) = \sin2 \theta – \sin \theta\) is maximum at \(\theta = 32^\circ 32′\). \begin{gather*} f(32^\circ 32′) = \sin(2\times 32^\circ 32′)-\sin(32^\circ 32′)=0.369\approx 0.37\\ \\ ∴ d_{\mathrm{max}} = 0.369R_{\mathrm{max}} < 0.37R_{\mathrm{max}} \end{gather*} That is, \(d\) must be less than \(37\%\) of the maximum possible range of the project to have a chance of hitting the target. |
(d)
| Let \(X\) be the random variable for the number of passengers that board a flight. Since every passenger has a \(5\%\) chance to miss a flight and hence a \(95\%\) chance to board the flight, then we have a binomial distribution with \(p=0.95\) and unknown \(n\). That is, \(X \sim \mathrm{Bin}(n,0.95)\).If we want to ensure that no more than \(1\%\) of the flights have more passengers showing up for the flight than the available 350 seats, then we want to find the largest \(n\) such that \[P(X>350) \leq 0.01\]We can approximate our binomial distribution with a normal distribution. To do so, we require the mean and variance of \(X\), \begin{align*} E(X) &= 0.95 n \\ Var(X) &= n(0.95)(0.05) = 0.0475n \end{align*} The binomially distributed random variable \(X \sim \mathrm{Bin}(n,0.95)\) can hence be approximated by a normally distributed random variable \(Y \sim \mathcal{N}(0.95n, 0.0475n)\). Applying continuity correction, \[P(X>350) \approx P(Y \geq 350.5)\] To get an upper tail probability of 0.01, we will examine the standard normal distribution table for the \(z\)-score that corresponds to \(0.99\), which is \(2.33\). Following the \(z\)-score formula, we hence have the equation \begin{align*} 2.33 = \frac{350.5 – 0.95n}{\sqrt{0.0475n}} \end{align*}Rearranging,\begin{align*} 2.33 \sqrt{0.0475} \sqrt{n} &= 350.5 – 0.95n \\ \\ 0.95n + 2.33 \sqrt{0.0475} \sqrt{n} – 350.5 &= 0 \end{align*}This is a quadratic in terms of \(\sqrt{n}\), so using the quadratic formula\begin{align*} \sqrt{n} &= \frac{-2.33\sqrt{0.0475} \pm \sqrt{(-2.33\sqrt{0.0475})^2 – 4(0.95)(-350.5)}}{2(0.95)} \\ \\ &= -19.4771\dots, \; 18.9425\dots \end{align*} Since \(\sqrt{n}\) can only be positive, then \begin{align*} n &= (18.9425\dots)^2 \\ \\ &\approx 358.82 \end{align*}Hence, we estimate 359 as the maximum number of tickets.Remark: \(n=359\) is the exact largest solution that ensures \(P(X>350) = \sum_{r=351}^n \binom{n}{r} 0.95^r 0.05^{n-r} \leq 0.01\). |
Written by Matrix Maths Team
The Matrix Maths Team are tutors and teachers with a passion for Mathematics and a dedication to seeing Matrix Students achieving their academic goals.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
